三角測量及其相關歷史（trigonometric measurement and its history)

Posted on 2010/12/03 in 三角函數, 函數, 數學 with 沒有迴響 7,824 views

三角測量及其相關歷史（trigonometric measurement and its history）
國立新竹高級中學數學科洪誌陽老師/國立臺灣師範大學數學系洪萬生退休教授責任編輯

一般而言，處理三角測量的問題 (對現行教材而言 )，是先將題目讀懂，轉化為數學，然後再透過解三角形的方式求得答案。不過學生遇到的，常是在設計好測量方式情境下，所處理的問題。其實，若在講解時可以從測量問題的原始狀況出發會別有一番風趣。在眾多版本中，康熙這部分的寫法最符合個原則值得參考。在底下將一些想法整理如下，供大家參考討論。

測量物體的高度、長度、寬度或深度，在很多問題中會被自然的提出，如土地測量、航海、天文觀測及地圖繪製等等。它最原始的問題應該是：我們如何用已知的知識去幫助我們知道待求物體的高度等等。

西方最早的記載是泰利斯(Thales)利用相似三角形來測得金子塔的高度，傳說他還曾經給出一種應用「邊角邊」的定理來計算船離河岸距離的方法，Katz在其《數學史通論》中有提出兩種猜想的方式，其實還蠻適合作為三角測量的開場。¹

原因之一當然是他回歸到了測量問題本身，另一是他並不是使用三角函數作為處理問題的工具。我們老師教學的結果，若是讓學生以為只有「三角」測量，那就頭痛了。當然，不用三角函數作測量的經典，當推中國發展出來的測量方式：「勾股」測量，若有時間，很可以作為三角測量的一個補充，至少也可以介紹一些資料給學生閱讀。²

另一個很好的例子，是西元前540年，希臘工程師尤帕林納斯（Eupalinos）奉命在薩摩的卡斯楚山兩側的城鎮開鑿引水隧道，以解決居民飲水問題。³ 此處，我們當然是簡化、改編了他原始的問題，提出底下的情境：

尤帕林納斯為了盡快的解決用水問題，他將工人分組成兩個團隊，從山的兩邊同時開挖，請問要如何給予兩組工人指示，才能合作的完成這項工程。（請注意，若放任兩組工人任意挖掘，導致水平方向或鉛直方向產生誤差，所挖的隧道就無法接起來，另一個問題是，隧道的總長當然是越短越好。）

每個人的策略可能不盡相同，不過這種開放性的問題，也許才能抓住測量的本質。當然，課綱的重點是在利用三角函數來解決測量問題，不過想讓學生能對這個方法產生感覺，知道它的優越性，前面的這個步驟可能還是無法省略。

在我們把焦點放在三角測量之前，再花幾句話談一談它重要的工具：正弦定理與餘弦定理。第一，並不是只有這兩個工具可以幫助我們做三角測量，例如，早期的課本也有提正切定理，但是，它們是最好用的兩個。第二，基本上，正弦定理與餘弦定理是等價的定理，也就是說，它們可以互相推導。⁴ 不過這兩種「形式」，在我們解三角形時，互補的很好。第三，這兩個定理，在希臘時代就已經被使用了，由天文學所提出的測量問題，在托勒密的《大成》（Almagest）中，至少已經等價的使用了餘弦與正弦定理。⁵它們之所以在解三角形時有用，也就是因為它們是透過實際問題所提出的解決「方案」。這兩個定理，與三角函數的一些基本概念，架構了高中的三角測量。

我們現在切入三角測量。我們若想測量一棟建築物的高度，最簡單的方式當然是從 \(A\) 點向前走距離 \(a\) 至底部 \(B\) 點，再測其對頂部 \(C\) 點的仰角 \(\theta\)，由此可以得到 \(h=(\tan\theta)a\)。

不過，我們常常無法如願的到達底部 \(B\) 點，所以，替代的方案是從 \(A\) 點向前走距離 \(a\) 至恰當的 \(D\) 點，不過，此時要多量一個角度，最簡單的是在 \(D\) 處量對頂部 \(C\) 點的仰角 \(\varphi\)，

因為 \(\overline{AB}=h\cot\theta\)，\(\overline{DB}=h\cot\varphi\)，
所以 \(\displaystyle h\cot\theta=a+h\cot\varphi\Longleftrightarrow{h}=\frac{a}{\cot\theta-\cot\varphi}\)

這個方式是三角測量常用的基本式子，很方便！

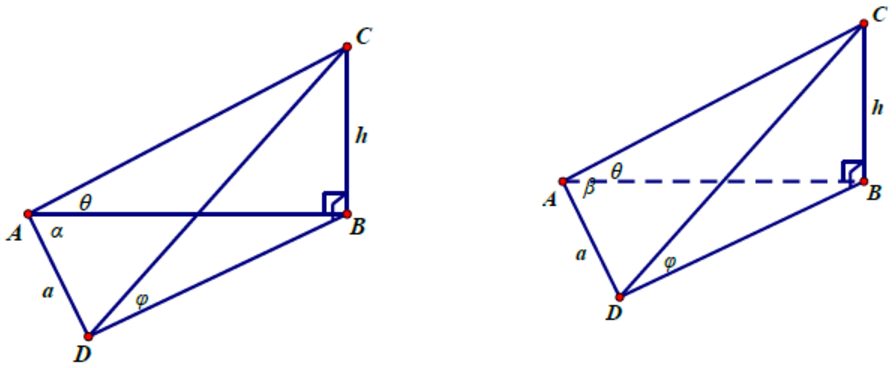
不過有時無法直接面對著 \(B\) 點直接走一段距離，譬如說這個方向的距離不夠長時，我們可以把平面圖擴展成立體圖，即走的並不是 \(\overleftrightarrow{AB}\) 的方向，如圖。此時因為資訊又不夠了，所以，可再量一個角度。例如我們量得 \(\angle{BAD}=\alpha\)，因為 \(\overline{AB}=h\cot{\theta}\)，\(\overline{DB}=h\cot{\varphi}\)，透過餘弦定理，我們可以列一個等式求解 \(h\)。

\((h\cot\varphi)^2=(h\cot\theta)^2+a^2-2(a)(h\cot\theta)\cos\alpha\)

又或者量得 \(\angle CAD=\beta\)，因為 \(\overline{AB}=h\csc\theta\)，\(\overline{DB}=h\csc\varphi\)，
我們可以得下列等式來求解 \(h\)。

\((h\csc\varphi)^2=(h\csc\theta)^2+a^2-2(a)(h\csc\theta)\cos\beta\)

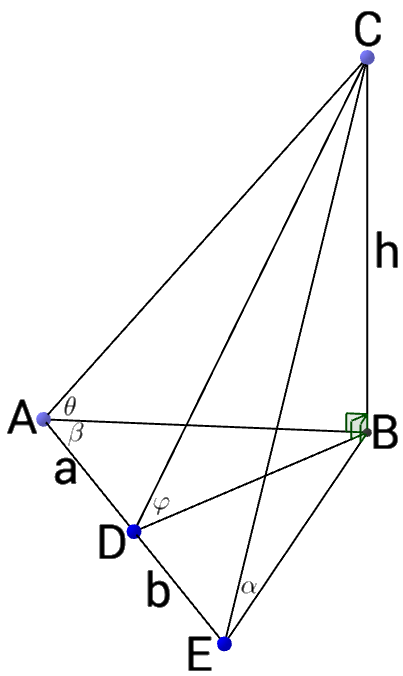
我們也可以從 \(D\) 再走一段距離 \(b\) 至 \(E\) 點，並測得其仰角為 \(\alpha\)，不過這樣還需要一個角，譬如我們量得 \(\angle{BAE}=\beta\)，因為 \(\overline{AB}=h\csc\theta\)，\(\overline{DB}=h\csc\varphi\)，\(\overline{EB}=h\csc\alpha\)，亦可列得一等式求 \(h\)。

\(\displaystyle\frac{(a)^2+(h\cot\theta)^2-(h\cot\varphi)^2}{2(a)(h\cot\theta)}=\frac{(a+b)^2+(h\cot\theta)^2-(h\cot\alpha)^2}{2(a+b)(h\cot\theta)}\)

前面這幾個圖在教材中均是常見，上面的建議只是提供一個流程來將它們一網打盡，而不是看成一個個單獨的例題。當然在真的測量時，還有很多問題待解決，例如角度的測量、(一般可能需要考慮到)測量者的高度或當地面不平坦時。有時量高轉成量寬時，也會有些許的差別，這都是不實際考慮就得不到的經驗。

在實際做角度的測量時，學生的誤差有時會很大，這當然跟他們的態度有關，不過有時也是因為他們所使用的工具。一般的建議，是透過量角器來做成一個簡單的工具，其方法為在中心處挖一個小孔並繫上一細繩，在繩子的另一端繫上一個重物。

測量時，將量角器 \(0^\circ\) 這一端靠近眼睛，另一端對準目標物觀測點。俯視目標物時，若細繩所示的角度為 \(\theta\)，俯角為 \((\theta-90^\circ)\)，仰視物體時，若細繩所示的角度為 \(\theta\)，可知仰角為 \((90^\circ-\theta)\)。