和算裡的弧長之冪級數公式(一)(The formula of arc length in the form of power series in Wasan Ⅰ)
和算裡的弧長之冪級數公式(一)
(The formula of arc length in the form of power series in Wasan Ⅰ)
臺北市立和平高中黃俊瑋教師
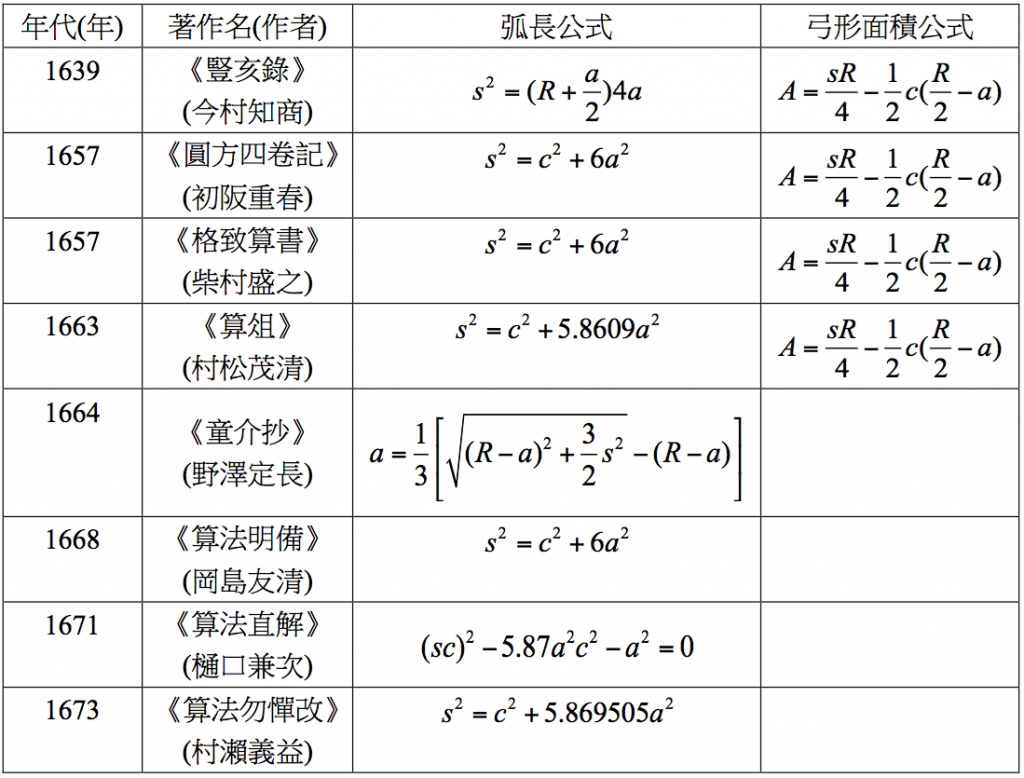
早在中國漢朝《九章算術》裡,便出現了圓面積及弓形面積公式,然而,後者所給的僅是近似公式。隨著中算書的傳入,江戶時期日本數學家們對於圓周率與弧長公式的研究,卻深感興趣。前者顯然受到中國的影響,後者卻是十足的和算產物。譬如說吧,十七世紀初期,今村知商的《豎亥錄》(1639)就提出了新的弧長公式(其中,我們以 \(R\) 表示圓之直徑、\(c\) 表示弦、\(a\) 表示矢、以 \(s\) 表示弧長):
\(s = \sqrt {(R + \frac{a}{2}) \cdot 4a}\)
當然,這同樣也只是近似公式。若我們進一步考察和算早期發展過程所出現的弧長公式,多與
\(s = \sqrt {{c^2} + ({\pi ^2} – 4){a^2}}\)
有關(如表一所示)。不過,若以後見之明來看,並不存在初等的弧長公式,因此,表一中的公式皆是近似公式。
在整個和算發展的歷史脈絡中,關孝和(Seki Takakazu, ?-1708)是開創關流,並奠下整個和算發展基礎最重要的數學家,他當然也針對弧長公式進行深入的研究,儘管他以招差法求得了更加精確的公式,不過,同樣只是近似公式。
一直得到1722年,建部賢弘(Takebe Katahiro, 1664~1739)所著的《綴術算經》以及宅間流的鐮田俊清所著的《宅間流圓理》,才分別以不同的方法求得了相當於冪級數形式的弧長公式,終得以解決了求弧長公式問題。其中,建部賢弘所得的公式為:
\({\left( {\frac{s}{2}} \right)^2} = Ra + \frac{1}{3}{a^2} + \frac{8}{{45}}{a^2}(\frac{a}{R}) + \frac{4}{{35}}{a^2}{(\frac{a}{R})^2} + \frac{{128}}{{1575}}{a^2}{(\frac{a}{R})^3} + \frac{{128}}{{2079}}{a^2}{(\frac{a}{R})^3} + …\)
他將弧長半冪 \((\frac{s}{2})^2\) 表示成徑(\(R\))與矢(\(a\))的無窮級數展開式。此公式可進一步表示成具遞迴關係的形式:
\({\left( {\frac{s}{2}} \right)^2} = Ra + \frac{1}{3}{a^2} + {D_1}\frac{8}{{15}}(\frac{a}{R}) + {D_2}\frac{9}{{14}}(\frac{a}{R}) + {D_3}\frac{{32}}{{45}}(\frac{a}{R}) + {D_4}\frac{{25}}{{33}}(\frac{a}{R}) + …\)
其中,\(D_0=Ra\)、\({D_k} = \frac{{2 \cdot {k^2}}}{{(k + 1)(2k + 1)}}{D_{k – 1}}(\frac{a}{R})\),\(k\) 為任意自然數。而這個公式與1737年由歐拉(Euler)與約翰.伯努利(Johann Bernoulli)所發現公式相同,可謂數學多元發現又一例。若以反三角函數與微積分的角度來看,它相當於 \((arc \sin\theta)^2\) 對 \(\theta\) 的冪級數展開式。
然而,建部賢弘造出此公式後,認為此公式「合半圓時,於矢之多者,用二差者盡二位;用三差者盡三位,用四差者盡四位,每增用一差(多)盡一位。……不密也。」亦即他對此公式並不滿意,他認為依此公式求弧背冪的精確速度不夠快,於是再造另一個具遞迴關係的公式:
\(\displaystyle\begin{array}{ll}{\left( {\frac{s}{2}} \right)^2} &= Ra + \frac{1}{3}{a^2} + {D_1}\frac{8}{{15}}(\frac{a}{{R – a}}) – {D_2}\frac{5}{{14}}(\frac{a}{{R – a}}) + {D_3}\frac{{12}}{{25}}(\frac{a}{{R – a}}) \\&~~~- {D_4}\frac{{223}}{{398}}(\frac{a}{{R – a}}) + \cdots\end{array}\)
其中,\(D_0=Ra\)、\({D_1} = \frac{1}{3}{a^2}\)、\({D_2} = {D_1}\frac{8}{{15}}(\frac{a}{{R – a}})\)、\(\cdots\)。同樣地,他仍不滿足於第二個公式的精確速度,於是再造出第三個公式:
儘管從第三個公式的前四項來看,難以寫出其一般式,不過,建部賢弘所用的方法可不斷地繼續造出第五項、第六項,當然往後各項之係數也更加複雜,且各項之間沒有明顯規律。最後,建部評論道:「用二差,所盡及原數之五差;用三差,所盡及原數之八差」,表明此公式的近似速度較前兩個公式快得多,因此建部賢弘至此方感到滿意。
參考文獻:
- 建部賢弘,《綴術算經》,1722年。
- 黃俊瑋,《關流算學研究及其歷史脈絡》,台灣師大數學系博士學位論文,2014。
- 表一參考自以下專書與論文:
- 徐澤林,《和算中源-和算算法及其中算源流》,頁299。
- 下平和夫,〈江戶初期的弧、矢、弦公式〉,《數學史研究》,1978(77)。
- 戶谷清一,〈江戶時代初期的數學書中有圓周率的研究〉,《數學史研究》,1980(87)。


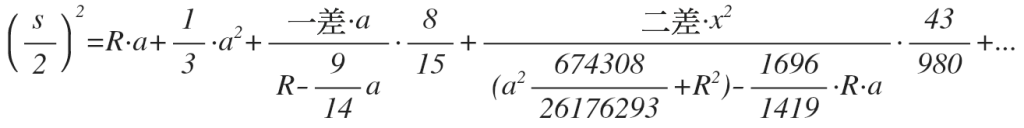
 前一篇文章
前一篇文章 下一篇文章
下一篇文章 泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2))  海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria)  惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題 
