從數學建模觀點看最「適配」直線(二)

Posted on 2014/08/26 in 數學, 數據分析, 機率統計 with 沒有迴響 3,528 views

從數學建模觀點看最「適配」直線(二)
（The best fit straight line in the view of mathematical modeling）
國立臺灣師範大學數學所博士班黃俊瑋

當我們觀察某組二維數據之散佈圖後，若發現這兩變數間呈現出正比趨勢，或具高度的直線相關時，自然會聯想到利用直線 \(y=\beta_0+\beta_1x\) 模型來適配這組二維數據。

假設這條理想的直線為 \(y=\beta_0+\beta_1x\)，數學上一般會利用最小平方法（least squares method）來探求此理想直線的參數 \(\beta_0\) 與 \(\beta_1\)。統計學裡，將每一筆資料 \((x_i,y_i)\) 的觀察值 \(y_i\) 與此直線的垂直差距稱為「殘差（residual）」，當然殘差平方越小，表示該筆資料與最佳直線的垂直距離也越小，即越接近該直線。

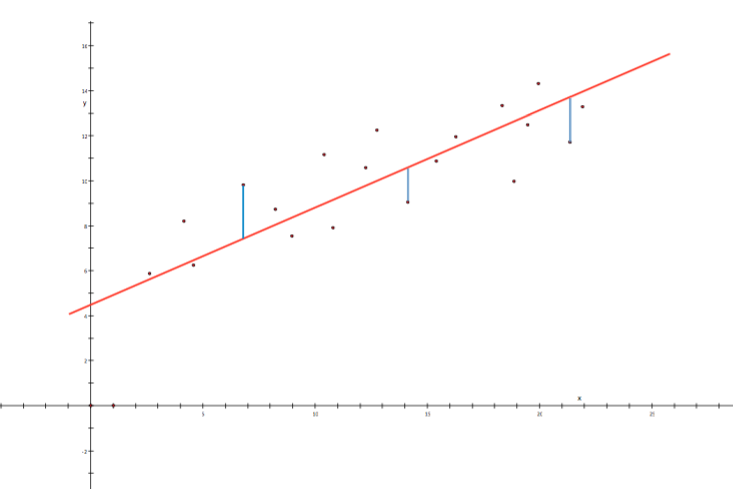
因此，直觀上我們不難想像，當一條直線能使得所有資料的殘差平方和越小，則此直線越「適配」這組資料，亦即適配度越佳（goodness of fit）。而所謂的最小平方法，本質上即是使得所有殘差之平方和最小時，所得之直線，此直線即為一般所謂的迴歸直線、最小平方直線或也被稱為最適配直線、最佳直線等。例如圖一當中的紅色直線即為這些數據的最適配直線，而藍色線段所示即當中某些資料 \(y_i\)的殘差。

至於如何實際推導、證明、求得此直線的過程或相關廻歸直線公式，讀者可參考一般高中教科書或大學統計教本，在此不贅述。統計上，估計參數，除了最小平方法之外，也有統計學家利用動差法（Method of Moment）或最大概似估計法（Maximum likelihood estimation）來求相關參數，不過相關概念涉及大學統計，在此亦不多討論，這裡僅提醒讀者最小平方法並非估計統計參數的唯一方法。

圖一某20筆觀察數據與其最適配直線

若從數學建模的觀點來看，依上述最小平方法實際求得了最適配直線 \(y=\beta_0+\beta_1x\) 之後，便相當於為這筆數據建立了一個數學模型。一般而言，當 \(X\) 與 \(Y\) 兩變數具高度直線相關性時，此直線與這些數據之間的「適配度」良好，這除了表示此直線對於這些資料而言，具代表性之外，我們也可以透過此直線進一步預測與推估，例如當 \(x\) 為某定值時，可利用此直線預測可能的 \(y\) 值。當然，實際觀測所得的 \(y\) 值未必等於最適直線上的 \(y\) 值，會因環境、實驗誤差、量測誤差等因素造成誤差的存在。

再者，此直線的斜率 \(\beta_1\) 說明了在變數 \(X\) 變動之下，變數 \(Y\) 相對應的變動程度，即當 \(X\) 變動 \(1\) 單位時，變數 \(Y\) 相對應的變動量。而此直線的截距 \(\beta_0\) 通常較不具重要意義，例如就體重（\(Y\)）對身高（\(X\)）的迴歸直線來看，\(\beta_0\) 可看成身高為 \(0\) 的人其體重的預測值，但此值顯然不具重要意義。

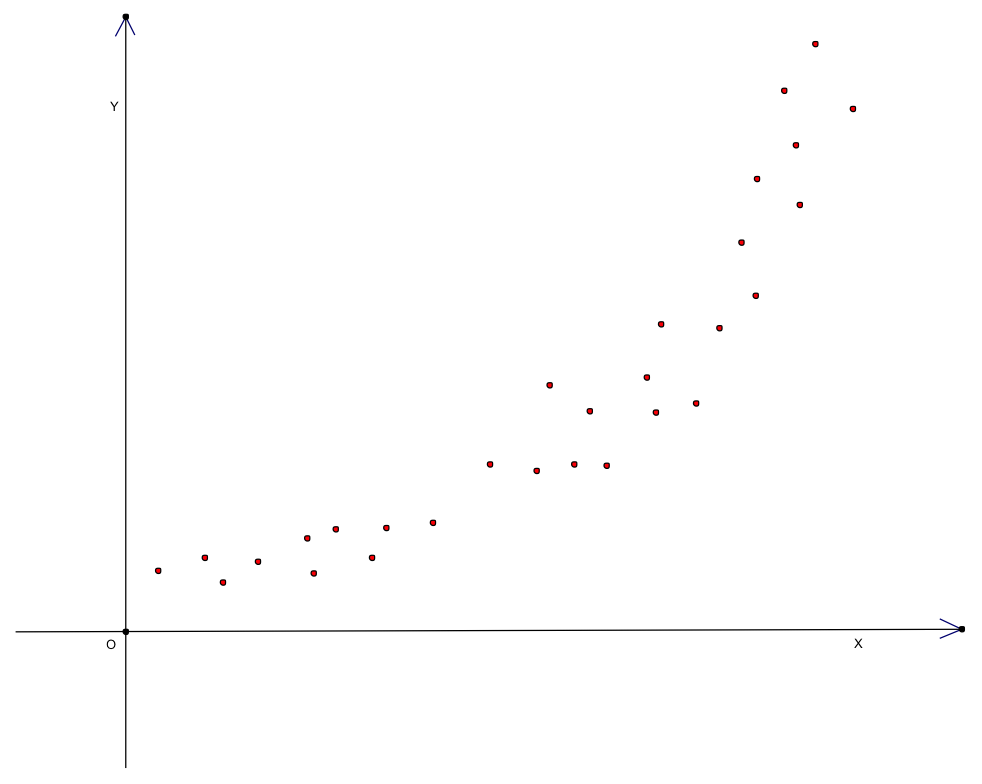
另一方面，如圖二與圖三所示為另外 \(30\) 筆觀察數據之散佈圖，從圖二散佈圖來看，不難發現其（直線）相關性不高，或從其相關係數之值接近 \(0\) 來看，可謂低度（直線）相關。這時，若貿然求其最適配「直線」事實上意義並不大，「適配度」不高且解釋與預測上皆有失偏頗。從這些散佈圖來看，不難發現圖三當中 \(X\) 與 \(Y\) 兩變量之間呈現出二次函數的趨勢，這時，適配圖二這 \(30\) 筆數據之數學模型不再是簡單線性模型，而應為二次曲線 \(y=\beta_0+\beta_1x+\beta_2x^2\)。