貝葉斯和貝氏定理(3)（Thomas Bayes and Bayes’ Theorem (3)）

貝葉斯和貝氏定理(3)（Thomas Bayes and Bayes’ Theorem (3)）
臺北市立第一女子高級中學蘇俊鴻老師

連結：貝葉斯和貝氏定理(2)

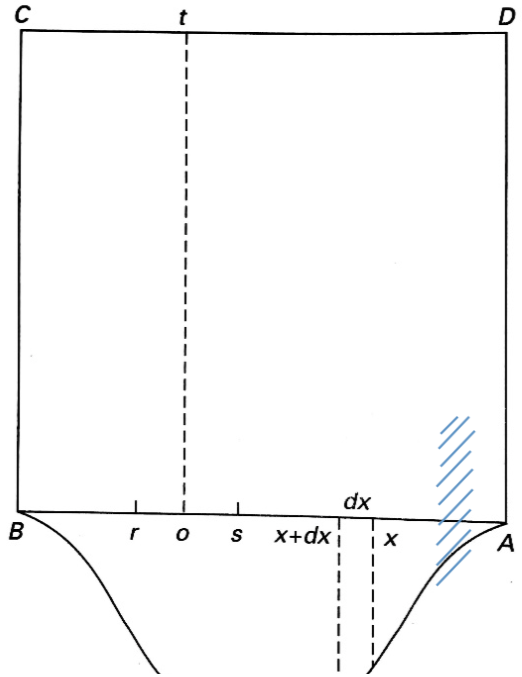
接著，我們來看貝葉斯如何求出 \(P(F)\) 和 \(P(E\cap F)\)。他用了一個頗為獨特的想法，據以建立機率模型進行計算。如圖一，考慮水平擺放一個正方形的桌面或平面 \(ABCD\)，將球 \(O\) 或 \(W\) 拋向桌面，並假設它們落在桌面上任何相等區域內的機率相同。

這時，假設球 \(W\) 先拋，過落點畫一條直線 \(ot\) 平行 \(AD\)，分別交 \(CD\) 與 \(AB\) 於 \(t\) 和 \(o\)。接著，球 \(O\) 被拋擲 \(p+q=n\) 次，如果它一次單獨拋擲中落在 \(AD\) 和 \(ot\) 之間，稱為在一次試驗中發生了事件 \(M\)。

圖一

為了便於接下來的說明，我們不妨設 \(\overline{AB}=1\)。依照貝葉斯的說法，球 \(W\) 的位置決定了機率 \(x\)。同時，點 \(o\) 落在點 \(r\) 與 \(s\) 之間的機率可以表示為 \(\overline{rs}\) 的長度。因此，在球 \(W\) 拋擲後，事件 \(M\) 的條件機率相當於 \(\overline{Ao}\) 的長度。

反過來說，任何給定一個機率範圍，都能用 \(\overline{AB}\) 上的一個區間來表示，記做 \([x,x + dx]\)，此時，\(x\) 值若視為球落在 \(ot\) 右側的機率，則 \(1-x\) 表示球落在 \(ot\) 左側的機率。

所以，在 \(p+q=n\) 次的拋擲中，球有 \(p\) 次落在 \(ot\) 右側的機率為

\(y = C_p^n{x^p}{(1 – x)^q} = C_p^n{x^p}{(1 – x)^{n – p}}\)

接著，貝葉斯在 \(\overline{AB}\) 的下方畫出 \(y = C_p^n{x^p}{(1 – x)^{n – p}}\) 對應的曲線(承自棣美弗的成果)。

由命題3知道，\(P(E \cap F) = P(E)P(F|E)\)。因此，球 \(W\) 落在區間 \([x,x + dx]\) 的上方，而球 \(O\) 有 \(p\) 次落在球 \(W\) 右側的機率可以用  \([x,x + dx]\) 下方與曲線之間所圍成的區域(斜線所示)面積表示。

所以，當 \(P(E \cap F) = P((r < x < s) \cap (X = p))\) 即為區間 \([r,s]\) 下方與曲線之間所圍的區域面積。以現在的符號即為

\(\int_r^s {C_p^n{x^p}{{(1 – x)}^{n – p}}dx}\)

同理，\(P(F) = P((0 < x < 1) \cap (X = p))\)，可以表為 \(\overline{AB}\) 與曲線之間所圍的區域面積，為

\(\int_0^1 {C_p^n{x^p}{{(1 – x)}^{n – p}}dx}\)

因此，由定理5可知，

\(\displaystyle P(E|F) = \frac{{P(E \cap F)}}{{P(F)}} = \frac{{\int_r^s {C_p^n{x^p}{{(1 – x)}^{n – p}}dx} }}{{\int_0^1 {C_p^n{x^p}{{(1 – x)}^{n – p}}dx} }}\)

依此結果，我們易知：事件 \(M\) 發生的機率，只要知道一定次數的試驗中發生與不發生的次數就能決定，不用知道更多其他的信息，透過上述面積的計算就能得到機率。

儘管貝葉斯形式上解決了這個問題，進入統計推斷的領域。但是，至少有兩個困難亟需跨越：首先，分子和分母涉及的面積計算(積分)並不容易。再來，對於上面這個推論的方式(等同一個思想實驗)，利用球的投擲滾動是否真的能代表實際情形嗎？而且，貝葉斯只考慮 \(X=0,1,2,\cdots,n\) 都具有相同的機率的情形，因為他覺得「沒有理由認為在一定次數的試驗中，它發生的次數會偏向某個可能的值，而不是其他的值。」這個假設引發不小的爭論：在不了解給定情形下發生事件的機率，就可以斷定所有可能的結果都具有相同的機率嗎？

而且，貝氏定理的核心概念是「先驗機率新獲得的資訊更新後的後驗機率」。這與二十世紀初期方興未艾，以頻率論(frequentism)為核心概念的統計學是相抵觸。可想而知，貝氏定理被長期冷落也就不意外。不過，進入二十一世紀，基於貝氏定理所發展的各式應用卻充斥在我們四周，如Google 搜索篩選詞條到無人駕駛汽車判斷自己的行駛位置等等。這又是另一段很長的故事，有興趣的讀者，可以參閱Sharon McGrayne所寫的《不死的定理》(The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy. Yale University Press, 2011. )

參考文獻：

• Katz, V. J. (1993), A History of Mathematics, New York: HarperCollins College Publishers.
• Biography of Thomas Bayes, http://www-history.mcs.st-and.ac.uk/Biographies/Bayes.html
• An Essay towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, F. R. S. Communicated by Mr. Price, in a Letter to John Canton, A. M. F. R. S. https://archive.org/stream/philtrans09948070/09948070#page/n0/mode/2up
• 陳昱成，〈貝氏定理的應用〉，《科學教育月刊》第357期(2013)，頁19-28。