分子速率的馬克士威分布

Posted on 2014/12/27 in 氣體動力論, 熱, 物理 with 有 1 則迴響。 20,396 views

分子速率的馬克士威分布 (Maxwell’s Distribution of Molecular Speed)
國立臺灣大學物理學系98級蔡亦涵

從小到大，班際運動會一定有一個項目─大隊接力，第一棒率先在跑道上奔馳，接著交給第二棒，繼續在跑道上揮灑青春的汗水，等到最後一棒跑回終點的那一剎那，裁判按下手中的碼錶，時間靜止那一刻，碼錶上面的數字記錄著我們一起完成的故事。這時候如果我們把總共跑的距離除以這個時間，會得到一個「速率」的概念，那這個速率代表什麼呢？其實這個速率是「平均速率」，也代表著平均每位選手的速率。

這時候問題就來了，既然這個叫做平均速率，難道大家都用這個速率在跑嗎？很明顯的，並不是每位選手都跑一樣的速率，其實大家有快有慢，這個「平均」代表的是我們這一個「群體」，「個別」是有差異的。

現在考慮一個方盒子，我們可以測得方盒子內的溫度，根據氣體動力論(kinetic theory of gas)，我們知道溫度跟分子速率有關，但我們測得的這個速率只能「代表群體」，如同上述大隊接力的例子，分子運動有快有慢，但分子的數目就這麼龐大，不可能知道每個分子運動的速率，更別說運動方向了，這個結果實在令人沮喪。

但上帝關上一扇門，一定會為我們開另一扇窗，這時候聰明的物理學家─馬克士威(Maxwell)和波茲曼(Boltzmann)，提出了統計力學(statistical mechanics)一個很重要的理論─馬克士威-波茲曼分布(Maxwell-Boltzmann distribution)：

\(\displaystyle\frac{N_i}{N}=\displaystyle\frac{e^{\displaystyle(-\frac{E_i}{kT})}}{\sum_j e^{\displaystyle(-\frac{E_j}{kT})}}\)

其中 \(N\) 代表總分子數，\(N_i\) 代表能量為 \(E_i\) 的分子數。

這個理論很重要的假設是：不考慮相對論效應、沒有量子現象、分子數量相當龐大且忽略除了碰撞之外的交互作用。這個公式描述了在某固定溫度 \(T\) 的情形下，各能量分子所佔有的比例，\(k\) 為波茲曼常數。現在我們把公式做個改寫，分子、分母同乘某個常數 \(C\)，使分母的數值變成 \(1\)，那麼公式變成：

\(\displaystyle\frac{N_i}{N}=Ce^{(\displaystyle-\frac{E_i}{kT})}\equiv P(E_i)\)

\(P(E_i)\) 代表能量為 \(E_i\) 的機率。更精確來說應該是機率密度(probability density)，大家如果第一次聽到這個名詞，可能會覺得很疑惑，以下就用一些圖來說明。

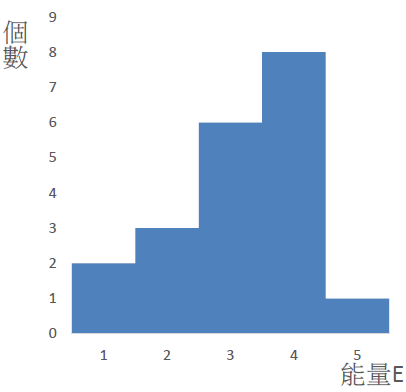
上圖總共有 \(20\) 個粒子，各能量具有的粒子數也都標示出來，現在以 \(E=2\) 為例，機率明顯看出是：

\(\displaystyle\frac{N_2}{N}=\frac{3}{20}\)

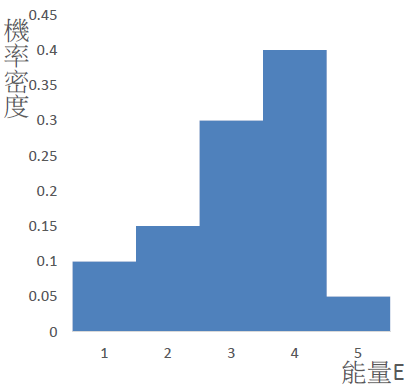
而這個算出來的數值恰巧等於 \(E=2\) 那條長條「面積」所佔整個藍色部分面積的比值，於是我們把圖轉換成這樣：

這樣就一目了然了，機率本身有「面積」的感覺，它是由「機率密度」乘以「底」得到的，因為現在能量是不連續的，每一個能量差都是 \(1\)，所以機率密度恰巧等於機率。

此時我們把能量當成連續分布，那麼在能量 \(E_i\) 附近的機率變成：

\(Ce^{(-\displaystyle\frac{E_i}{kT})}\mathrm{d}E\)

現在我們想要知道速率的分布，於是我們把 \(E_i\) 用 \(\frac{1}{2}m(v_x^2+v_y^2+v_z^2)\) 代入，因為有三個方向，所以機率寫成：

\(Ce^{(-\displaystyle\frac{\frac{1}{2}m(v_x^2+v_y^2+v_z^2)}{kT})}\mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_z\)

分別對三個方向積分，積分範圍皆為 \(-\infty\) 到\(\infty\)，且機率的總和必須為 \(1\)，於是：

\(\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}Ce^{(-\displaystyle\frac{\frac{1}{2}m(v_x^2+v_y^2+v_z^2)}{kT})}\mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_z=1\)

經過整理我們得到機率密度：

\(P(v_x,v_y,v_z)=\sqrt{\displaystyle\frac{m}{2\pi kT}}^3e^{(-\displaystyle\frac{m(v_x^2+v_y^2+v_z^2)}{2kT})}\)

這個方程式告訴我們各個分量的機率密度，但是我們比較感興趣的是速率，即為速度大小，不管他的方向，於是我們有以下式子：

\(\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\sqrt{\frac{m}{2\pi kT}}^3e^{(-\frac{m(v_x^2+v_y^2+v_z^2)}{2kT})} \mathrm{d}v_x\mathrm{d}v_y\mathrm{d}v_z=\int_{0}^{\infty}\sqrt{\frac{m}{2\pi kT}}^3e^{(-\frac{mv^2}{2kT})}4\pi v^2 \mathrm{d}v\)

這是將直角坐標系的積分轉換成球座標系的積分，經過整理：

\(\int_{0}^{\infty}\displaystyle\sqrt{\frac{m}{2\pi kT}}^3e^{\displaystyle(-\frac{mv^2}{2kT})}4\pi v^2 \mathrm{d}v=\int_0^{\infty}P(v)\mathrm{d}v\)

我們可以得到跟分子速率有關的機率分布：

\(P(v)=\displaystyle\sqrt{\frac{2}{\pi}(\frac{m}{kT})^3}v^2e^{(\frac{-m}{2kT})v^2}\)

這就是分子速率的馬克士威分布(Maxwell’s Distribution of Molecular Speed)。

這個機率密度公式告訴我們，在某個溫度 \(T\) 的情形下，分子速率為 \(v\) 所佔有的機率密度。我們可以利用這個公式進一步算出哪個速率的機率最高、平均速率、方均根速率等等，如下所示，其中方均根速率不偏不倚等於氣體動力論裡面推導過的方均根速率。

機率最大的速率 \(V_p=\displaystyle\sqrt{\frac{2kT}{m}}\)

平均速率\(V_m=\displaystyle\sqrt{\frac{8kT}{m}}\)

方均根速率 \(V_{rms}=\displaystyle\sqrt{\frac{3kT}{m}}\)

有趣的是，就算我們有能力在一開始時故意安排氣體分子，讓它們不滿足馬克士威(也等同於馬克士威-波茲曼)分布，但氣體分子還是會透過大量的碰撞去交換能量與動量，於是在經過一小段時間後，系統就滿足馬克士威分布了！這可以從圖3的電腦模擬中看出來(圖3是個很大的檔案，約25MB，故建議讀者下載回去自行觀看動畫)。