比例檢定

比例檢定(Test of Proportions)
國立臺灣大學農藝學系 吳博雅

一、前言

常常市面上一些電子產品宣稱其不良率低於一個目標值（例如：5%），或是一個好的棒球打擊者其打擊率高達七成以上，或是要判定新藥的使用可以使疾病的死亡率降低至九成以下等相關問題，其實都屬於單組樣本比例檢定的問題。若是要探討舊藥與新藥對疾病治癒率的差異性，或是探討兩射箭選手命中紅心射擊率的差異性等相關問題，屬於兩組樣本比例檢定的問題。比例檢定是針對取樣自二項分布的樣本，假設於大樣本情況下，依據中央極限定理，樣本比例會近似於常態分布，並且分成「單一組樣本比例檢定」與「兩組樣本比例檢定」這兩部分做更進一步的介紹。

二、單一組樣本比例檢定

假設 \(X_1,X_2,…,X_n\) 均來自伯努力試驗 (Bernoulli trials) 結果，亦即 \(X_i=0\) 或 \(1\)； \(0\) 表示試驗結果為「失敗」，\(1\) 表示試驗結果為「成功」，一共取 \(n\) 個樣本，其成功的機率為 \(p\)。若 \(n\) 次試驗中共有 \(k\) 次成功，其樣本比例為 \(\hat{p}=\frac{\sum^{n}_{i=1}x_i}{n}=\overline{x}=\frac{k}{n}\)。

當樣本數 \(n\) 夠大時（通常指符合 \(np > 5\) 且 \(n(1-p) > 5\) 兩個條件），根據中央極限定理，\(\hat{p}\) 會近似於常態分配 \(N(p,\frac{p(1-p)}{n})\)，如圖一。因此將 \(\hat{p}\) 進行標準化 \(\frac{\hat{p}-p}{\frac{p(1-p)}{n}}\sim N(0,1)\)，可利用該式對比例 \((p)\) 進行統計推論，一共有二大步驟：

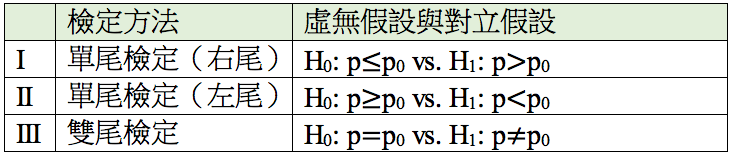
步驟一：建立虛無假設與對立假設，又可分為單尾檢定（右尾與左尾）與雙尾檢定之情況，如表一。

表一、三種不同情下的虛無假設與對立假設。（本文作者吳博雅製）

步驟二：進行決策，可以利用統計量、p-value以及信賴區間來評估，如表二。

表二、三種不同情況下的 Z 統計量、p-value 與信賴區間，以及決策方式。（本文作者吳博雅製）

圖一、樣本數 n 夠大時，樣本比例近似常態分布。（本文作者吳博雅製）

例題：（以參考文獻 1之例 8.2a 作為介紹）

一般患肺癌病人 3 年內之死亡率超過 90%，今有新療法，一共試驗 150 位肺癌病人，3 年內有 126 位病患死亡，想要知道新療法是否有較好的效果。（設 \(\alpha=0.05\)）

<解>

\(\hat{p}=\frac{126}{150}=0.84\)，\(Var(\hat{p})=\frac{p_0(1-p_0)}{n}=\frac{0.9\times 0.1}{150}=0.0006\)

\((1)\) \(H_0:p=p_0=0.9~~~vs.~~~H_1:p\ne p_0\)

\((2)\) \(\displaystyle Z_0=\left|\frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}\right|=\left|\frac{0.84-0.9}{\sqrt{0.0006}}\right|=2.450>Z_{0.025}=1.96\)

p-value \(=0.00714<\alpha=0.05\) （使用 excel 的函數：1-NORMSDIST\((Z_0)\)）

\(p\) 之 95% 信賴區間為 \(\begin{array}{ll}\displaystyle[\hat{p}-Z_{\frac{\alpha}{2}}\sqrt{\frac{p_0(1-p_0)}{n}},\hat{p}+Z_{\frac{\alpha}{2}}\sqrt{\frac{p_0(1-p_0)}{n}}]\\= [0.84-1.96, 0.84+1.96]\\= [0.792,0.888]\end{array}\)

因為 \(Z_0>Z_{0.025/2}\)，且 p-value \(<\alpha=0.05\)，又因 \(p\) 之 95% 信賴區間不含 \(0.9\)，故拒絕 \(H_0\)，代表該新藥有療效。

三、兩組樣本之比例檢定

如上段落所提，由二項族群中，獨立取得兩筆資料，分別為 \(X_1\) 與 \(X_2\)，其樣本大小分別 \(n_1\) 與 \(n_2\)，成功的機率分別為  \(p_1\) 與 \(p_2\)，亦即 \(X_1\sim B(n_1,p_1)\)，\(X_2\sim B(n_2,p_2)\)，假設該兩筆資料分別成功的次數為 \(k_1\) 與 \(k_2\)，其樣本比例分別為 \(\hat{p_1}=\frac{k_1}{n_1}\) 與 \(\hat{p_2}=\frac{k_2}{n_2}\)，當 \(n_1\) 與 \(n_2\) 夠大時，\(\hat{p_1}\) 與 \(\hat{p_2}\) 會近似於常態分布。而兩樣本比例差 \(\hat{p_1}-\hat{p_2}\)仍為近似常態分布，其 \(E(\hat{p_1}-\hat{p_2})=p_1-p_2\)，\(Var(\hat{p_1}-\hat{p_2})=\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}\)。

若欲探討兩筆資料的 \(p_1\) 與 \(p_2\) 有無差異，其假設檢定為：

\(H_0:p_1-p_2=(p_1-p_2)_0~~~~vs.~~~~H_1:p_1-p_2\ne(p_1-p_2)_0\)

接下來進行決策：

\((1)\) Z 值：

\(\displaystyle Z_0=\frac{(\hat{p_1}-\hat{p_2})-(p_1-p_2)_0}{\displaystyle\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}}=\frac{(\hat{p_1}-\hat{p_2})-(p_1-p_2)_0}{\displaystyle\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}}>Z_{\alpha/2}\)，

則拒絕 \(H_0\)。

因為 \(p_1\) 與 \(p_2\) 未知，用樣本的估值 \(\hat{p_1}\) 與 \(\hat{p_2}\)代替之。

\((2)\) p-value：p-value \(= 2P(Z>|Z_0|)<\alpha\)，則拒絕 \(H_0\)。

\((3)\) \(p_1p_2\) 之 \((1-\alpha)\%\) 信賴區間：

\(\displaystyle[(\hat{p_1}-\hat{p_2})-Z_{\frac{\alpha}{2}}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}},(\hat{p_1}-\hat{p_2})+Z_{\frac{\alpha}{2}}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}]\)

例題：（以參考文獻 1之例 8.7 作為介紹）

某農藥商宣稱，其新農藥比舊農藥的殺蟲效果高出 8%，今將此兩農藥施用於昆蟲，結果如下表三：\((\alpha=0.05)\)

表三、新藥與舊藥殺蟲的效果。（資料來源：參考文獻 1）

<解>

\((1)\) \(H_0:p_1-p_2=0.08~~~~vs.~~~~H_1:p_1-p_2\ne 0.08\)

p-value \(=0.0116 <\alpha=0.05\)

\(p_1-p_2\) 之 95% 信賴區間為

\(\displaystyle[(\hat{p_1}-\hat{p_2})-Z_{\frac{\alpha}{2}}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}},(\hat{p_1}-\hat{p_2})+Z_{\frac{\alpha}{2}}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}]\)

\(\displaystyle= [(0.8-0.6)-1.96\sqrt{\frac{0.8\times 0.2}{400}+\frac{0.6\times 0.4}{100}},(0.8-0.6)+1.96\sqrt{\frac{0.8\times 0.2}{400}+\frac{0.6\times 0.4}{100}}]\)

\(= [0.0963,0.3037]\)

因 \(Z_0>Z_{0.025/2}=1.96\)，且 p-value \(< 0.05\)，又因 \(p_1-p_2\) 之 95% 信賴區間不含 \(0.08\)，故拒絕 \(H_0\)，代表新農藥比舊農藥的殺蟲效果的確高出至少 \(8\%\)。

參考文獻

1. 沈明來 (2014)。生物統計學入門。九州。
2. 郭寶錚、陳玉敏 (2011)。生物統計學。五南。
3. Hogg, R., Tanis, E., Zimmerman, D. (2015). Probability and Statistical Inference 9^th
4. 陳順宇、鄭碧娥 (2004)。統計學（第四版）。華泰。