排容原理(Principle of Inclusion and Exclusion)(一)
排容原理(Principle of Inclusion and Exclusion)(一)
國立高雄大學應用數學系游森棚副教授責任編輯
排容原理( Principle of Inclusion and Exclusion, 簡稱PIE),是高中排列組合的第三個,也是最後一個基礎原理(前兩個是「乘法原理(Rule of Product)」與「加法原理 (Rule of Sum)」) 亦有一些書按英文順序直譯為容斥原理(或許這是比較好的翻譯)。
排容原理中的「排」 是指「排除」,「容」是指「容納」。 基本上的想法就是「多退少補」 — 多算的要排除,少算的要加進來。從原文亦可以清楚看出這個原理的精神。
高中數學的排容原理,課堂上的實際教學不外乎從介紹下列式子開始:
$$| {A} \cup {B} | = |{A}| + |{B}| – |{A} \cap {B} |~~~~~~~~~(1)$$
老師的講解都是用文氏圖(Venn diagram) 來說明的,這是直觀而容易懂的好方法:
接著例題可能就是「國文及格有 $$30$$ 人,數學及格有 $$20$$ 人,兩科都及格有 $$15$$ 人,問至少一科及格有幾人?」。 緊接著必定會介紹三個集合的排容原理,一樣會利用文氏圖來說明:
$$| {A} \cup {B} \cup {C} | = |{A}| + |{B}| + |{C}| – |{A} \cap {B} | – |{B} \cap {C} |- |{A} \cap {C} | + |{A} \cap {B} \cap {C}|~~~(2)$$
高中的排容原理,事實上教到這裡已經非常足夠了。但一些教師可能會接著介紹一般性的結果,也許這樣講:“同理可證,四個集合的排容原理如下”:
$$(3)$$
$$\begin{array}{ll}|{A}\cup{B}\cup{C}\cup{D} |&=|{A}| +|{B}|+|{C}|+|{D}| – |{A} \cap {B}| – |{A} \cap {C}| – |{A} \cap {D}| \\&- |{B} \cap {C}| – |{B} \cap {D}| – |{C} \cap {D}| + |{A} \cap {B} \cap {C}| +|{A} \cap {B} \cap {D}| \\&+ |{A} \cap {C} \cap {D}| + |{B} \cap {C} \cap {D}| – |{A} \cap {B} \cap {C} \cap {D}|\end{array}$$
學生多半能從上述三個式子中看出規則,老師最後就會說「一般來說,有以下的排容原理」:
$$(4)$$
$$\begin{array}{ll}|A_1\cup\cdots\cup A_n|&=(|A_1|+\cdots+|A_n|)-(|A_1\cap A_2|+\cdots+|A_{n-1}-A_n|)\\&+(|A_1\cap A_2\cap A_3|+|A_1\cap A_2\cap A_4|+\cdots+|A_{n-2}\cap A_{n-1}\cap A_{n}|)\\&-\cdots+(-1)^{n+1}|A_1\cap \cdots \cap A_n|\end{array}$$
口頭上會加上說明:「一個一個加(所以一共 $$\left( \begin{array}{c} {n}\\ {1} \end{array}\right)$$),減去兩個兩個交集(所以一共減去 $$\left( \begin{array}{c} {n}\\ {2} \end{array}\right)$$) 項),加回來三個三個交集(所以加回來 $$\left( \begin{array}{c} {n}\\ {3} \end{array}\right)$$ 項),再減去四個四個…」。
這樣的教學無可厚非,師生都滿意,皆大歡喜。
但是,以上的教學過程卻有兩個很大的盲點一直被忽略。
第一個盲點,以兩個集合為例。我們都知道,將 $$(1)$$ 式兩邊用宇集(universal set) $${S}$$ 去減,再於左式用笛摩根定律(De Morgan law, $$\overline{({A} \cup {B})} = \overline{A} \cap \overline{B}$$)後可以得到下式:
$$| \overline{A} \cap \overline{B}|=|{S}| – |{A}|-|{B}| + |{A} \cap {B}|~~~~~~~~~(5)$$
這當然也可以用文氏圖說明。這個例題會是「全班有 $$50$$ 人,國文及格有 $$30$$ 人,數學及格有 $$20$$ 人,兩科都及格有 $$15$$ 人,問兩科都不及格有幾人?」
好,問題來了。到底 $$(1)$$ 式是排容原理,還是 $$(5)$$ 式是排容原理?
筆者曾經對一群約五十位現任高中數學老師作調查,答案是一面倒認為 $$(1)$$ 式才是排容原理。但是並非如此!!排容原理原始的精神是要算「這個條件也不成立,那個條件也不成立」 的方法數,而不是算「至少有一個條件成立的方法數」。 因此嚴格說起來,
$$| \overline{A} \cap \overline{B}|=|{S}| – |{A}|-|{B}| + |{A} \cap {B}|$$ 才是排容原理
而「$$|{A} \cup {B}| = |{A}| + |{B}| – |{A} \cap {B}|$$」是「排容原理的對偶形式(dual form)」!
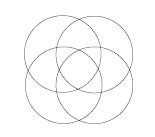
第二個盲點,三個集合的 $$(2)$$ 式可以用文氏圖說明是三個圓畫出來剛好把平面分成八塊,但是,如果讀者曾試著去畫四個圓交出來的文氏圖,就會驚愕地發現,四個圓最多只能把平面分成 $$14$$ 塊!要用文氏圖說明,必須要有 $$16$$ 個區域!所以,從三個集合的 $$(2)$$ 式到四個集合的 $$(3)$$ 式,並不能「同理可證」!
因此證明四個集合以上的排容原理(或是對偶的排容原理),並不是「同理可證」或「一般來說」 就可以矇過去的。這是需要一點功夫的。我們將在下一篇文章中討論。
連結:排容原理(二)


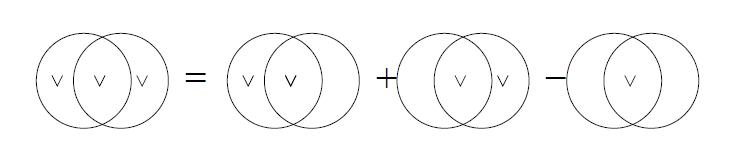

 前一篇文章
前一篇文章 下一篇文章
下一篇文章 海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria)  惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題  泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2)) 
