和算中的行列式(3)：關孝和的《解伏題之法》（下）（Determinants in Wasan (3): Seki Takakazu’s Kai Fukudai no Ho (Methods of Solving Secret Questions), Part 2）

Posted on 2014/08/10 in 數學, 數學史 with 沒有迴響 1,812 views

和算中的行列式(3)：關孝和的《解伏題之法》（下）（Determinants in Wasan (3): Seki Takakazu’s Kai Fukudai no Ho (Methods of Solving Secret Questions), Part 2）
國立臺南第一高級中學林倉億老師

連結：和算中的行列式(2)：關孝和的《解伏題之法》（上）

〈和算中的行列式(2)：關孝和的《解伏題之法》（上）〉介紹了關孝和如何從解多元高次方程組中，發展出類似今日行列式的概念。然而，即便是今日，多元高次方程組求解仍是一件困難的工作。所以，關孝和能處理多元高次方程組，更顯得他在數學上的造詣深厚。以下透過幾個簡單的實例，讓讀者更熟悉關孝和的方法，也指出這個方法也有無能為力的時候。

例1：解 $$\left\{ \begin{array}{l} {(x – 1)^2} + {(y – 1)^2} = 1\\ {(x – 2)^2} + {(y – 2)^2} = 5\\ {(x – 3)^2} + {(y – 3)^2} = 13 \end{array} \right.$$。

【關孝和的方法】：

方程組可整理成 $$\left\{ \begin{array}{l} ({y^2} – 2y + 1) – 2x + {x^2} = 0\\ ({y^2} – 4y + 3) – 4x + {x^2} = 0\\ ({y^2} – 6y + 5) – 6x + {x^2} = 0 \end{array} \right.$$，

利用係數所成行列式 $$\left| {\begin{array}{*{20}{c}} {{y^2} – 2y + 1}&{ – 2}&1\\ {{y^2} – 4y + 3}&{ – 4}&1\\ {{y^2} – 6y + 5}&{ – 6}&1 \end{array}} \right| = 0$$，

但左式展開後各項均消去，得到 $$0=0$$ 的恆等式，而非 $$y$$ 的方程式，因此無從求 $$y$$ 之值。

【幾何意義】：

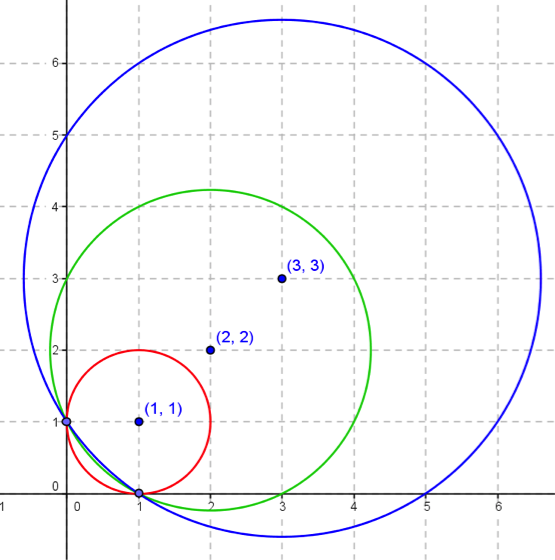
三個方程式的代表的圖形都是圓形，圓心分別是 $$(1,1)$$、$$(2,2)$$、$$(3,3)$$，

半徑依序是 $$1$$、$$\sqrt 5$$、$$\sqrt{13}$$，圖形如下：

這三個圓均交於 $$(1,0)$$、$$(0,1)$$ 兩點，因此 $$(x,y)=(1,0)$$、$$(0,1)$$ 是方程組的兩組解。

例2：解 $$\left\{ \begin{array}{l} {(x – 1)^2} + {(y – 1)^2} = 1\\ {x^2} + {y^2} = 1\\ {(x + 1)^2} + {(y + 1)^2} = 1 \end{array} \right.$$。

【關孝和的方法】：

方程組可整理成 $$\left\{ \begin{array}{l} ({y^2} – 2y + 1) – 2x + {x^2} = 0\\ ({y^2} – 1) + 0x + {x^2} = 0\\ ({y^2} + 2y + 1) + 2x + {x^2} = 0 \end{array} \right.$$，

利用係數所成行列式 $$\left| {\begin{array}{*{20}{c}} {{y^2} – 2y + 1}&{ – 2}&1\\ {{y^2} – 1}&0&1\\ {{y^2} + 2y + 1}&2&1 \end{array}} \right| = 0$$，

得到 $$8 = 0 \to\leftarrow $$，故此題無解。

【幾何意義】：

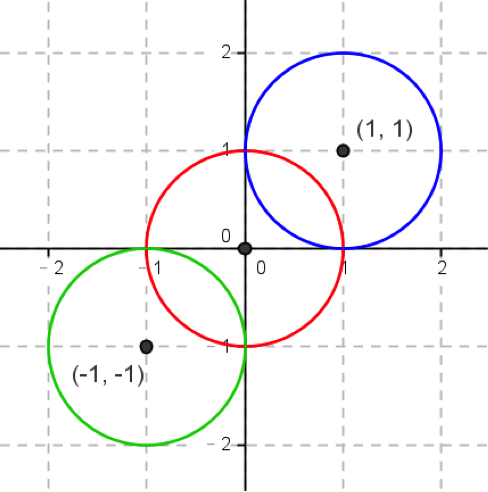
三個方程式的代表的圖形都是圓形，圓心分別是 $$(1,1)$$、$$(0,0)$$、$$(-1,-1)$$，

半徑都是1，三個圓並沒有共同的交點，故方程組無解。圖形如下：

例3：解 $$\left\{ \begin{array}{l} {x^2} + {y^2} = 1\\ 4{x^2} + {y^2} – 4 = 0\\ {y^2} – 4x + 4 = 0 \end{array} \right.$$。

【關孝和的方法】：

方程組可整理成 $$\left\{ \begin{array}{l} ({y^2} – 1) + 0x + {x^2} = 0\\ ({y^2} – 4) + 0x + 4{x^2} = 0\\ ({y^2} + 4) – 4x + 0{x^2} = 0 \end{array} \right.$$，

利用係數所成行列式 $$\left| {\begin{array}{*{20}{c}} {{y^2} – 1}&0&1\\ {{y^2} – 4}&0&4\\ {{y^2} + 4}&{ – 4}&0 \end{array}} \right| = 0 \Rightarrow 12{y^2} = 0\Rightarrow y = 0\Rightarrow x = 1$$。

【幾何意義】：

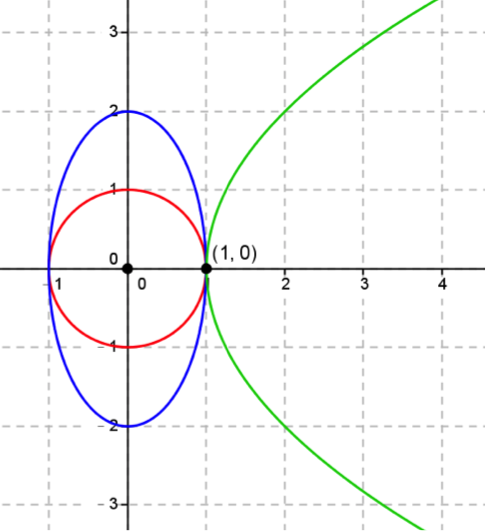
三個方程式的代表的圖形分別是圓形、橢圓與拋物線，只相交於 $$(1,0)$$，

故 $$(1,0)=(x,y)$$ 是方程組的唯一解。圖形如下：

例4：解 $$\left\{ \begin{array}{l} {x^2} + {y^2} = 1\\ 4{x^2} + {y^2} – 4 = 0\\ {y^2} – 4x + 8 = 0 \end{array} \right.$$。

【關孝和的方法】：

方程組可整理成 $$\left\{ \begin{array}{l} ({y^2} – 1) + 0x + {x^2} = 0\\ ({y^2} – 4) + 0x + 4{x^2} = 0\\ ({y^2} + 8) – 4x + 0{x^2} = 0 \end{array} \right.$$，

利用係數所成行列式 $$\left| {\begin{array}{*{20}{c}} {{y^2} – 1}&0&1\\ {{y^2} – 4}&0&4\\ {{y^2} + 8}&{ – 4}&0 \end{array}} \right| = 0\Rightarrow 12{y^2} = 0\Rightarrow y = 0\Rightarrow x = 1\to \leftarrow $$

因為 $$x=1,y=0$$ 代入第三個方程式 $$y^2-4x+8=0$$ 不合。

【幾何意義】：

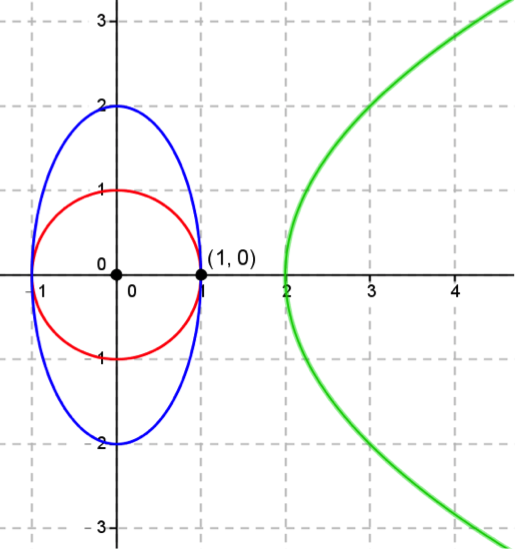
三個方程式的代表的圖形分別是圓形、橢圓與拋物線，但沒有共同的交點，故方程組無解。

圖形如下：

由上述4個例子可看出，利用係數行列式等於 $$0$$ 不一定能求得的 $$y$$ 的方程式，

就算可以，解出的 $$y,x$$ 仍要代回原方程組檢驗，不一定都會符合。

那為什麼會有不合的情形出現呢？

我們可以換個方式來看關孝和的方法，就是將方程組整理成後，

若將 $$x^2$$ 看成變數 $$y’$$，那麼由三個二元一次方程組要有共同的解，得到係數行列式

說巧不巧，這恰好就是萊布尼茲發展出行列式概念的方式，請參見本網站〈行列式的濫觴：萊布尼茲 (1)、(2)〉。東、西方行列式的開創者，竟然可以在這裡「合鳴」！

但問題來了，$$y’=x^2$$ 並不是與 $$x$$ 獨立的變數，因此，利用求得的解，

仍必須代回原方程組檢驗是否有不合的情形出現。

簡言之，多元高次方程組的題目，會隨著條件的多寡（方程式的數目）而有不同的解，甚至解法還會相當繁雜。比如說，當未知數個數不只兩個的時候，就要反覆消去未知數個數才行。

例如關孝和與兩個學生建部賢明、建部賢弘所寫的《大成算經》中，就有這麼一個相當於四元四次方程組 $$\left\{ \begin{array}{l} {x_1}^4 + {x_2}^3 + {x_3} + {x_4} = {A_{1}}\\ {x_1}^3 + {x_2}^2 + {x_3}^3 + {x_4}^4 = {A_{2}}\\ {x_1}^2 + {x_2} + {x_3}^4 + {x_4}^3 = {A_{3}}\\ {x_1} + {x_2}^4 + {x_3}^2 + {x_4}^2 = {A_{4}} \end{array} \right.$$ 的問題，轉載於下，讓有興趣的讀者挑戰看看！

假如有甲乙丙丁平方各一。甲云：甲方三乘冪[註：四次方]、乙方再乘冪[註：三次方]、丙方、丁方相併共若干；乙云：甲方再乘冪、乙方冪[註：二次方]、丙方再乘冪、丁方三乘冪相併共若干；丙云：甲方冪、乙方、丙方三乘冪、丁方再乘冪相併共若干；丁云：甲方、乙方三乘冪、丙方冪、丁方冪相併共若干。問甲方？

連結：和算中的行列式(4)：降階展開法

參考資料：