數學之旅：三角形面積公式(I)

數學之旅：三角形面積公式(I)
(Mathematical Journey through the Formulas of Triangle Area)
國立蘭陽女中陳敏晧教師

三角形面積公式是數學中面最常用的公式，也是大家在小學學數學的甜蜜記憶。

希臘哲人柏拉圖曾說：「畫在沙地上的三角形可以被抹去，但是，三角形的觀念不會受時間與空間的限制而留存下來。」可見三角形的觀念與發展會隨著人類數學發展而不斷變化。但是，不論如何演變，數學的新論點卻永遠根植於舊有的基礎上。

從個人學習數學的歷程看來，三角形的面積公式就如同是典範(paradigm)般的重要。我們可以透過公式的演變來重新釐清學習的轉移(shift)；當吾人從數學史的知識論脈絡切入，會發現三角形的面積公式從幾何學出發，邁向三角學領域，接引向量，拓展行列式，認識內積與外積，於解析幾何處發揚光大。接著就開始我們的數學之旅：

1. 從幾何學出發：三角形面積等於底邊乘底邊上高的一半。
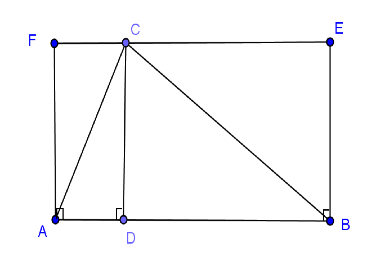
   如圖一解釋，不失其完整性，本文的三角形均以銳角三角形為例說明。
   \(\begin{array}{ll}a\Delta ABC &= a\Delta ADC + a\Delta BCD \\&= \frac{1}{2}\overline{AD}\cdot\overline {DC}+ \frac{1}{2}\overline {DB}\cdot\overline {DC}\\&= \frac{1}{2}(\overline{AD}+\overline {DB})\cdot\overline {DC}\\&= \frac{1}{2}\overline {AB}\cdot\overline {CD}\end{array}\)
   上式的 \(a\) 代表三角形的區域面積。
   

   圖一

   根據小學數學課綱，小學生是在四年級學習到三角形面積等於底邊乘底邊上高的一半。但是一直到了高中二年級，學習到三角函數，才又有新的面積公式出現。

2. 利用正弦定義求得三角形面積：
   若 \(\Delta ABC\) 的三邊長 \(\overline {BC}= a,\overline {CA}= b,\overline {AB}= c\)，
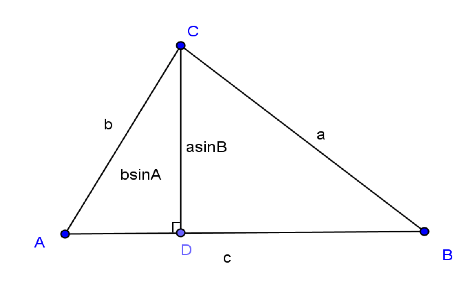
   則  \(a\Delta ABC = \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B\)
   

   圖二

   證明：如上圖二，
   因為 \(\sin A = \frac{{\overline {CD}}}{{\overline {AC} }}\)，所以高 \(\overline {CD}= \overline {AC}\cdot \sin A = b\sin A\)。
   因此，\(a\Delta ABC = \frac{1}{2}\overline {AB}\cdot \overline {CD}= \frac{1}{2}bc\sin A\)；
   若根據 \(\sin B = \frac{{\overline {CD} }}{{\overline {BC} }}\)，所以，高 \(\overline {CD}= \overline {BC}\cdot \sin B = a\sin B\)。
   因此，\(a\Delta ABC = \frac{1}{2}\overline {AB}\cdot \overline {CD}= \frac{1}{2}ac\sin B\)；
   同理可證 \(a\Delta ABC = \frac{1}{2}ab\sin C\)，
   最後得 \(a\Delta ABC = \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B\)。

   這個面積公式的特徵在於
   當讀者知道 \(\Delta ABC\) 的兩個邊 \(a\) 與 \(b\)，及夾角 \(\angle C\)，即是 \(SAS\) 定理，便可以確定三角形面積。

3. 利用正弦定理求得三角形面積：
   若 \(\Delta ABC\) 的三邊長 \(\overline {BC}= a,\overline {CA}= b,\overline {AB}= c\)，
   則 \(a\Delta ABC = \frac{1}{2}{c^2} \cdot \frac{{\sin A\sin B}}{{\sin (A + B)}} = \frac{1}{2}{b^2} \cdot \frac{{\sin A\sin C}}{{\sin (A + C)}} = \frac{1}{2}{a^2} \cdot \frac{{\sin B\sin C}}{{\sin (B + C)}}\)證明：
   根據三角形的正弦定理 \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)，所以，\(a = b \cdot \frac{{\sin A}}{{\sin B}}\) 代入，
   \(\begin{array}{ll}a\Delta ABC &= \frac{1}{2}ab\sin C \\&= \frac{1}{2}b \cdot \frac{{\sin A}}{{\sin B}} \cdot b\sin C \\&= \frac{1}{2}{b^2} \cdot \frac{{\sin A\sin C}}{{\sin ({{180}^0} – (A + C))}} \\&= \frac{1}{2}{b^2} \cdot \frac{{\sin A\sin C}}{{\sin (A + C)}}\end{array}\)
   同理可證 \(a\Delta ABC = \frac{1}{2}{c^2} \cdot \frac{{\sin A\sin B}}{{\sin (A + B)}} = \frac{1}{2}{a^2} \cdot \frac{{\sin B\sin C}}{{\sin (B + C)}}\)

   這個面積公式的特徵在於
   當讀者知道 \(\Delta ABC\) 的兩個角 \(\angle A\) 與 \(\angle C\)，及夾邊 \(b\)，即是 \(ASA\) 定理，便可以確定三角形面積。
   當然我們也可以將此公式表示為 \(a\Delta ABC = \frac{1}{2}{c^2} \cdot \frac{{\sin A\sin B}}{{\sin C}} = \frac{1}{2}{b^2} \cdot \frac{{\sin A\sin C}}{{\sin B}} = \frac{1}{2}{a^2} \cdot \frac{{\sin B\sin C}}{{\sin A}}\)
   不過在實際上運算而言，相較於 \(a\Delta ABC = \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B\)
   而言是不常用的面積處理方法，充其量僅能當公式推論練習。

總之，本文章先從底邊乘底邊上高的一半來探索三角形的面積公式，接著將對應高利用正弦定義來轉換，最後引用正弦定理來導出三角形面積公式。在第二篇文章時，我們著眼於三角形的三邊長，將從海龍公式出發，並比較一下秦九韶的三斜求積術的公式。

連結：數學之旅：三角形面積公式(II) 

參考文獻：

1. William Dunham著，林傑斌譯，
   《天才之旅(Journey Through Genius :The Great Theorems of Mathematics )》，台北：牛頓出版社，1995。
2. http://en.wikipedia.org/wiki/Triangle