型 I 錯誤、型 II 錯誤與 p 值

型 I 錯誤、型 II 錯誤與 p 值(Type I Error, Type II Error, and p-value)
國立臺灣大學農藝所生物統計組碩士班 陳丘原

假設檢定是先對母體參數提出假設，然後利用樣本的資訊，再決定是否接受或否決該假設；而在進行假說檢定的決策時，可能會犯兩種錯誤（表一）：

一、型 I 錯誤 (Type I Error)：

若 \(\mathrm{H_0}\)（虛無假說）為真，但結論卻否決 \(\mathrm{H_0}\)，則犯了第一型錯誤，而稱犯第一型錯誤的機率為第一型錯誤率 (Type I Error Rate)，其發生的機率以 \(\alpha\) 表示，或稱顯著水準 (significant level)。

二、型 II 錯誤 (Type II Error)：

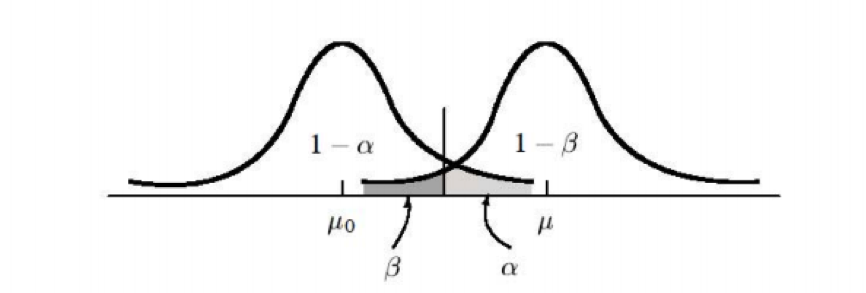
若 \(\mathrm{H_1}\)（對立假說）為真，但結論卻接受 \(\mathrm{H_0}\)，則犯了第二型錯誤，而稱犯第二型錯誤的機率為第二型錯誤率 (Type II Error Rate)，其發生的機率以 \(\beta\) 表示。另外，統計上常稱 \(1-\beta\) 為檢定力 (Power)（圖一）。

表一、型 I 錯誤與型 II 錯誤概念表。（本文作者陳丘原製）

型 I 與型 II 錯誤若干性質如下：首先，\(\alpha\) 與 \(\beta\) 互為拮抗，亦即 \(\alpha\) 提高時、\(\beta\) 降低；反之亦然。統計學上認為犯型 I 錯誤的後果相當嚴重，因此一般希望能將其發生的機率 \((\alpha)\) 控制在一定的程度 \((0.05~or~0.01)\)。當固定 \(\alpha\) 時，可透過增加樣本數達到降低 \(\beta\) 的目的。

圖一、型 I 錯誤與型 II 錯誤示意圖（圖片來源：參考文獻 1）

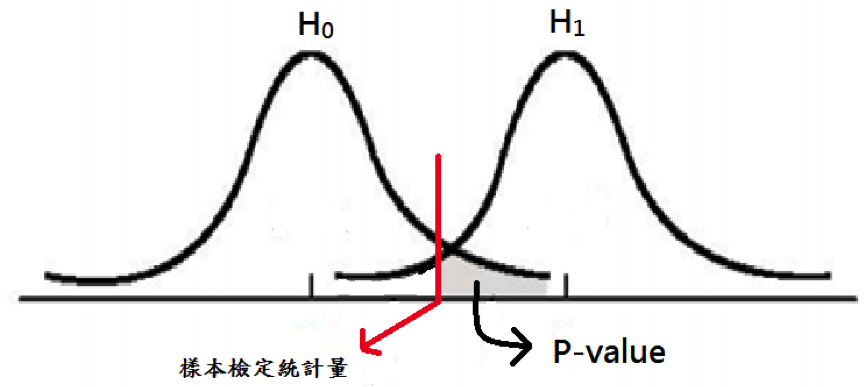
另外，在進行假說檢定時，p 值 (p – value) 也是一種幫助我們下決策的指標；p 值的定義為: 在 \(\mathrm{H_0}\)（虛無假說）成立的情況下，檢定統計量的取樣分布中往 \(\mathrm{H_1}\) 方向超過或等於實際觀測到之檢定統計量值的尾端機率（圖二灰色部分）。p – value 可用來在任何顯著水準下作檢定，若 p – value \(\le \alpha\) 決策為棄卻 \(\mathrm{H_0}\)；若 p – value \(>\alpha\) 決策為在 \(\alpha\) 的顯著水準下，不棄卻 \(\mathrm{H_0}\)。

圖二、p 值示意圖。（本文作者陳丘原繪）

p 值應用在假設檢定之決策範例

一、某公司想了解在雞飼料中加入魚骨粉後，對雞每月平均產蛋量是否提高。以一般飼料餵食每隻雞之每月平均產蛋量為 \(\mu_0=20\) 個，標準偏差 \(\sigma=9\)。今試驗 \(100\) 隻雞，把魚骨粉加入飼料中餵食後，每隻雞之每月平均產蛋量為 \(\overline{X}=25\)，試問添加魚骨粉是否能提升雞隻產蛋量?

根據題意，其虛無假說 \(\mathrm{(H_0)}\) 及對立假說 \(\mathrm{(H_1)}\) 分別為：

\(\mathrm{H_0}:\mu=20\)

\(\mathrm{H_1}:\mu>20\)

若訂定顯著水準 \(\alpha = 0.05\)，並計算檢定統計量（Z 值）為

\(\displaystyle Z_0=\frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}=\frac{25-20}{9/\sqrt{100}}=5.5556\)

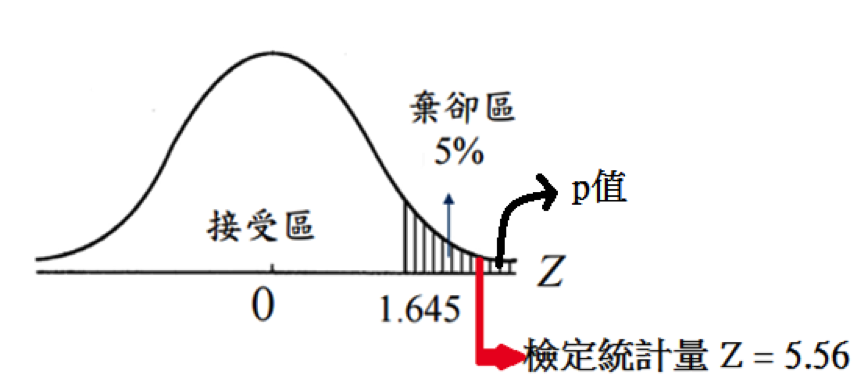
假設以上 \(Z_0\) 統計量服從標準常態分布，則此檢定的 p 值為任一標準常態分布的隨機變數 \(Z\) 「大於或等於 \(Z_0\)」（往 \(\mathrm{H_1}\) 方向超過或等於實際觀測到之檢定統計量值）的機率（圖三）：

p-value \(= P(Z > 5.5556) = 1.38\times 10^{-8}< 0.05\)

圖三、單尾檢定及p值示意圖。（本文作者陳丘原繪）

因此，本檢定應拒絕 \(\mathrm{H_0}\)，即添加魚骨粉的確能提升雞隻產蛋量。

二、某計程車公司有一整隊車輛，過去幾年的紀錄是平均每輛車每個月行駛距離為 \(2500\) 英里。今欲檢定目前每輛車每個月行駛的英里數是否不同於過去的 \(2500\) 英里，於是隨機取樣 \(n = 40\) 輛車，記錄其目前每輛車每個月行駛的英里數，加以平均得 \(\overline{y}=2750\) 英里（已知族群標準差維持在 \(\sigma=350\) 英里）。

根據題意，其虛無假說 \(\mathrm{(H_0)}\) 及對立假說 \(\mathrm{(H_1)}\)分別為:

\(\mathrm{H_0}:\mu=2500\)

\(\mathrm{H_1}:\mu\ne 2500\)

若訂定顯著水準 \(\alpha = 0.05\)，並計算檢定統計量（Z 值）為

\(\displaystyle Z_0=\frac{\overline{y}-\mu_0}{\sigma/\sqrt{n}}=\frac{2750-2500}{350/\sqrt{40}}=4.5175\)

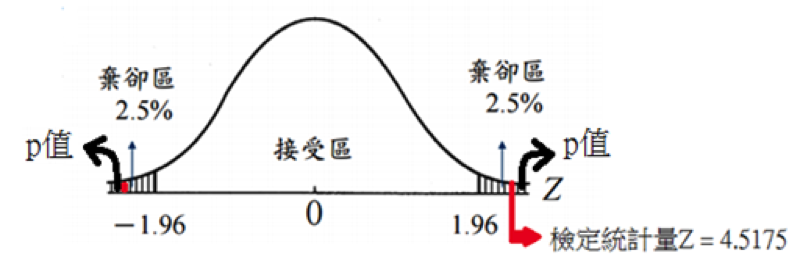
假設以上 \(Z_0\) 統計量服從標準常態分布，則此檢定的 p 值為任一標準常態分布的隨機變數 Z「等於 \(Z_0\)」、「大於 \(Z_0\)」或「小於 \(-Z_0\)」（往 \(\mathrm{H_1}\) 方向超過或等於實際觀測到之檢定統計量值）的機率（圖四）：

圖四、雙尾檢定及 p 值示意圖（本文作者陳丘原繪）

\( \begin{array}{cl}
\text{p-value} & =P(Z\ge 4.5175)+P(Z\le -4.5175) \\
&= 2\times P(Z\ge 4.5175)\text{(標準常態分布以零為中心、左右對稱)}\\
&= 6.26\times 10^{-6}<0.05
\end{array} \)

因此，本檢定應拒絕 \(\mathrm{H_0}\)，即目前每輛車每個月行駛的英里數不同於過去的 \(2500\) 英里。

參考文獻

1. 沈明來 (2014)。生物統計學入門第六版。第七章-假設檢定。九州。
2. 郭寶錚、陳玉敏 (2011)。生物統計學。第十章-假設檢定。五南。