微積分的dx(二)：從級數到函數論
微積分的dx(二)：從級數到函數論 李龍欣 上回我…
微積分
微積分的dx(一)：無限小數與非標準分析學
微積分的dx(一)：無限小數與非標準分析學
李龍欣
17世紀時牛頓和萊布尼茲發明了微積分。其中萊布尼茲的「積分符號」\(\int\)、「極微小差」\(dx\) 等兩個符號仍然使用至今。現今的課本會用「極限」解釋，所以有些人說 \(dx\) 只是符號，不需要實質意義。這兩種觀點都有其意義和重要性。本文將分為若干期，從不同觀點探索微積分的靈魂、以及各觀點的應用。
●為何有微積分
自古以來，數學家們就深知自然萬物難以測量，而不如圓形、多邊形、橢圓一般簡潔。我們固然可以拿起一把尺開始耐著性子量，例如阿基米德 (Αρχιμήδης ο Συρακούσιος)、劉徽、關孝和 (関 孝和) 的割圓術，又譬如古巴比倫人的三角函數表，都是測量的典範和先驅。
從牛頓的時代背景探索第二運動定律（下）
從牛頓的時代背景探索第二運動定律（下）
行政院科技部科技顧問／瑞典林雪平大學榮譽教授 趙光安
牛頓給力一個定義：第二運動定律
在伽利略和牛頓的時代，數學工具只有幾何、三角、和代數，物理知識也僅限日常生活中有系統的觀察，及少數的實驗結果。用現代的標準來衡量，伽利略和牛頓頂多只有國中畢業的程度。如果我們用現代的數理常識背景來解答三、四百年前的問題，那就是「事後有先見之明」了。雖然和「力學」有關的量測，伽利略得到的數據被推崇是權威性，然而他的「力學」實驗幾乎全部是基於物體的直線運動。在這個時代背景下，牛頓建立的理論，是從「一維系統」開始，然後才推廣到「三維空間」。因此，我們也從直線運動開始，試試看能否經歷一趟牛頓的思路。
泰勒多項式(2) （Taylor Polynomials(2)）
泰勒多項式(2) （Taylor Polynomials(2)）
臺北市立第一女子高級中學蘇俊鴻老師
連結：泰勒多項式(1) （Taylor Polynomials(1)）
在〈泰勒多項式(1)〉中，我們提到：
任意實係數 \(n\) 次多項式 \(f(x)\)，定能表成 \(f(x)\) 在 \(x=a\) 處的泰勒多項式
\(\begin{multline*}\displaystyle f\left( x \right) = f\left( a \right) + \frac{{f’\left( a \right)}}{{1!}}\left( {x – a} \right) + \frac{{f”\left( a \right)}}{{2!}}{\left( {x – a} \right)^2} + \frac{{f”’\left( a \right)}}{{3!}}{\left( {x – a} \right)^3} \\+\cdots+\frac{{{f^{\left( n \right)}}\left( a \right)}}{{n!}}{\left( {x – a} \right)^n}\end{multline*}\)
這個定理對於我們回頭解決多項式的問題，或是研究多項式的性質很有幫助，本文的目的，就是提出泰勒多項式的幾個應用。
泰勒多項式(1) （Taylor Polynomials(1)）
泰勒多項式(1) （Taylor Polynomials(1)）
臺北市立第一女子高級中學蘇俊鴻老師
請考慮下面的問題：
已知多項式函數 \(f(x)=-x^3+5x^2-8x+4\)，求 \(f(0.99)\) 的值（四捨五入取到小數點以下第二位）。
儘管將 \(x=0.99\) 代入，即可求出函數值。
但 \(f(0.99) =- {(0.99)^3} + 5 \times {(0.99)^2} – 8 \times (0.99) + 4\) 繁複計算過程令人卻步。
因此，處理這類問題，通常採取下面的作法
- 步驟一：將 \(f(x)\) 表示成 \(f(x) = a + b(x – 1) + c{(x – 1)^2} + d{(x – 1)^3}\)，
計算出 \(a,b,c,d\) 各值。此題的結果 \(a=0,b=-1,c=2,d=-1\) - 步驟二：將 \(x=0.99\) 代入，即可估取近似值。
以上題為例，由步驟一知，\(f(x) =- (x – 1) + 2{(x – 1)^2} – {(x – 1)^3}\)。所以，
\(\begin{array}{ll} f(0.99) &=-(0.99-1)+2\times{(0.99-1)^2}-{(1-0.99)^3}\\&=-(0.01)+2\times{(0.01)^2}-{(0.01)^3}\\&\approx -(0.01)=-0.01\end{array}\)
由步驟二的數值計算來看，應能推敲步驟一將原多項式改寫成以 \((x-1)\) 的冪次方升冪排列的多項式之用意。不過，進一步思考，上述解法正表明：當 \(1-\varepsilon\le x\le 1+\varepsilon\)，其中的 \(\varepsilon\) 為足夠小的正數時，有 \(f(x)\approx -(x-1)\)。
如何過圖形上一點求切線方程式(2)（Finding an equation of the tangent line to the curve at the given point(2)）
如何過圖形上一點求切線方程式(2)
（Finding an equation of the tangent line to the curve at the given point(2)）
臺北市立第一女子高級中學蘇俊鴻老師
接續〈如何過圖形上一點求切線方程式(1)〉最後提出的問題，本文的目的就是介紹微積分如何解決這些難題。首先，我們必須澄清什麼是切線？不能再像過去訴諸圖形直觀，需要對「切線」這個概念賦予明確的定義。我們想要在圖形上一點找到它的切線，因難之處在於我們需要相異兩點才能決定直線，如何能用「切點」定義呢？當然，微積分為我們解決這個困難。
切線的定義
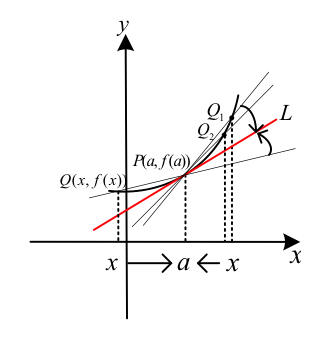
如圖一，設 \(f(x)\) 為一函數，\(P(a,f(a))\) 是 \(y=f(x)\) 圖形上一定點。
在 \(P\) 點附近找圖形上異於 \(P\) 的一點 \(Q(x,f(x))\)，連接 \(P,Q\) 可得一割線 \(PQ\)。
當 \(Q\) 點沿著圖形以 \(Q_1,Q_2,\cdots\) 向 \(P\) 點趨近時，能得到一連串的割線 \(PQ_1,PQ_2,\cdots\)。
若 \(Q_n\) 沿著圖形趨近 \(P\) 時，割線 \(PQ_n\) 的極限直線 \(L\) 存在﹐
則稱直線 \(L\) 為 \(y=f(x)\) 圖形上過 \(P\) 點的切線﹐並稱 \(P\) 為切點。也就是說，
割線 \(PQ\xrightarrow{Q\rightarrow P}\)過 \(P\) 點的切線
圖一
如何過圖形上一點求切線方程式(1)（Finding an equation of the tangent line to the curve at the given point(1)）
如何過圖形上一點求切線方程式(1)
（Finding an equation of the tangent line to the curve at the given point(1)）
臺北市立第一女子高級中學蘇俊鴻老師
給定一條曲線圖形(通常可視為函數圖形的一部份)，如何求出過圖形上一點的切線方程式？切線問題有著實際應用的對應。例如，運動物體在任意瞬間的運動方向，就是運動軌跡在那一點的切線方向。或是光學透鏡設計需要求出曲面的法線，而法線與切線垂直；若能求出切線，也就決定法線。
這些都是十七世紀當時科學研究和應用的一部份，這些需求促動微積分技術的發展，經過眾人的改進與演化，補強技術的理論，最終發展出微積分這一門優美又有威力的學問。靜心想想，討論「求切線方程式」問題一直是高中數學的主題之一，其解決方法的流變，頗有顯現此種數學知識積累的過程。因此，本文特意將高中數學中相關題材蒐集討論，以饗讀者。
微積分初階－歷史發展的眼光（1）前言（First Course in Calculus－A Historical Approach 1. Introduction
這是關於微積分一系列文章的第一篇，微積分是高中基礎數學的總結，更是進入現代數學之門。本文淺談函數的重要性，並藉由它在微積分當中所扮演的角色，簡單介紹何謂微分與積分。數、函數、空間是數學研究的主要對象，分別發展出代數學、分析學與幾何學。函數（function）是微積分的主角。我們要對函數做微分並且做積分，然候作各種的應用，包括應用到數學本身以及大自然的變化與運動現象。
函數的重要性是，它們代表著自然律（laws of nature）或是更廣泛的數學律（laws of mathematics），反應著數學、自然或人文現象的量與量之間的關係，表現為各種模型（models）。函數有無窮多，其中只有少數有名字、有公式，大多數是屬於沒有名字、沒有公式的無名英雄。
在有名字、有公式的函數中，我們最熟悉的是：多項函數、三角函數、指數函數、對數函數、雙曲三角函數、有理函數、無理函數、．．．等。這些函數也是微積分要研究的首要對象。
微積分初階－歷史發展的眼光（2）促動微積分誕生的四類問題（First Course in Calculus－A Historical Approach 2.Four kinds of problems in Calculus
微積分的誕生具有長遠的歷史發展過程，本文提及促成微積分誕生的四類問題：「求積問題」、「求切線問題」、「求極值問題」以及「研究物體的運動問題」。此四類問題可歸結為求積與求切線兩大問題，前者發展出「積分學」，後者則發展出「微分學」。問題是數學探索與思考的出發點。數學之發源於問題，就好像人類古文明之發源於大河旁一般，非常自然。提出問題，再尋求問題的解答（The art of problem posing and problem solving）乃是啟開智慧與思想的最佳法門。更確切地說，數學是人類在長期探索自然的過程中，不時地叩問自然乃至逼問自然，所創造發展出來的產物。
到底是哪些問題促成了微積分的誕生呢？微積分起源於要解決下面四類古老而實用的問題，人們才創造出解決問題的概念與方法，經過長久的改進與演化，終於發展出一門深刻而漂亮的有系統學問。