如何過圖形上一點求切線方程式(2)（Finding an equation of the tangent line to the curve at the given point(2)）

如何過圖形上一點求切線方程式(2)
（Finding an equation of the tangent line to the curve at the given point(2)）
臺北市立第一女子高級中學蘇俊鴻老師

連結：如何過圖形上一點求切線方程式(1)

接續〈如何過圖形上一點求切線方程式(1)〉最後提出的問題，本文的目的就是介紹微積分如何解決這些難題。首先，我們必須澄清什麼是切線？不能再像過去訴諸圖形直觀，需要對「切線」這個概念賦予明確的定義。我們想要在圖形上一點找到它的切線，因難之處在於我們需要相異兩點才能決定直線，如何能用「切點」定義呢？當然，微積分為我們解決這個困難。

切線的定義

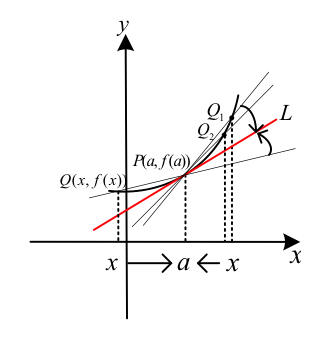
如圖一，設 \(f(x)\) 為一函數，\(P(a,f(a))\) 是 \(y=f(x)\) 圖形上一定點。
在 \(P\) 點附近找圖形上異於 \(P\) 的一點 \(Q(x,f(x))\)，連接 \(P,Q\) 可得一割線 \(PQ\)。
當 \(Q\) 點沿著圖形以 \(Q_1,Q_2,\cdots\) 向 \(P\) 點趨近時，能得到一連串的割線 \(PQ_1,PQ_2,\cdots\)。
若 \(Q_n\) 沿著圖形趨近 \(P\) 時，割線 \(PQ_n\) 的極限直線 \(L\) 存在﹐
則稱直線 \(L\) 為 \(y=f(x)\) 圖形上過 \(P\) 點的切線﹐並稱 \(P\) 為切點。也就是說，

割線 \(PQ\xrightarrow{Q\rightarrow P}\)過 \(P\) 點的切線

圖一

因此，透過極限的概念，就能利用割線 \(PQ\) 定義出切線。同樣地，將割線 \(PQ\)的斜率取極限，自然就是切線的斜率。換言之

割線 \(PQ\) 斜率 \(\frac{{f(x) – f(a)}}{{x – a}}\xrightarrow{Q\rightarrow P}\) 過 \(P\) 點的切線斜率 \(\mathop {\lim }\limits_{x \to a} \frac{{f(x) – f(a)}}{{x – a}}\)

事實上，當函數 \(f(x)\) 在 \(x=a\) 處及 \(a\) 附近有意義，且 \(\mathop {\lim }\limits_{x \to a} \frac{{f(x) – f(a)}}{{x – a}}\) 存在時，我們稱函數 \(f(x)\) 在 \(x=a\)處可微分。而這個極限稱為 \(f(x)\) 在 \(x=a\) 處的導數，以符號 \(f'(a)\) 表示。

因此，函數 \(f(x)\) 圖形過點 \((a,f(a))\) 的切線斜率就是導數 \(f'(a)\)。所以，只要會求導數，切線方程式的問題就輕鬆解決了。

舉個例子，說明用微積分解切線問題

已知函數 \(y=x^3-3x^2+1\)

1. 求在 \(x=2\) 的導數 \(f'(2)\)。
2. \(P(2,-3)\) 為 \(y=x^3-3x^2+1\) 圖形上一點，求以 \(P\) 點為切點的切線 \(L\) 方程式。
3. 切線 \(L\) 與函數 \(y=x^3-3x^2+1\) 的圖形是否有其他交點？

從問題(1)開始，想要求導數，可以由導數的定義著手

\(\begin{array}{ll}f'(2) &= \mathop {\lim }\limits_{x \to 2} \frac{{f(x) – f(2)}}{{x – 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{({x^3} – 3{x^2} + 1) – ( – 3)}}{{x – 2}}\\&= \mathop {\lim }\limits_{x \to 2} \frac{{{x^3} – 3{x^2} + 4}}{{x – 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{(x – 2)({x^2} – x – 2)}}{{x – 2}} \\&= \mathop {\lim }\limits_{x \to 2} ({x^2} – x – 2) = 0\end{array}\)

當然，若知道如何求導函數的話，也能微分求出導函數，再代入求導數。

\(y = f(x) = {x^3} – 3{x^2} + 1 \Rightarrow f'(x) = 3{x^2} – 6x \Rightarrow f'(2) = 3 \times {2^2} – 6 \times 2 = 0\)

求出導數後，問題(2)變得容易多了。由(1)知，過點 \(P(2,-3)\) 的切線斜率為 \(f'(2)=0\)，因此，以 \(P\) 為切點的切線方程式為 \(y=-3\)。

最後，問題(3)求兩圖形的交點，就是解聯立方程

\(\left\{ \begin{array}{l} y = {x^3} – 3{x^2} + 1\\ y = – 3 \end{array} \right. \\\Rightarrow {x^3} – 3{x^2} + 1 = – 3 \Rightarrow {(x – 2)^2}(x + 1) = 0\)
\(\Rightarrow x=2\) 或 \(x=-1\)。

所以還有另一個交點 \((-1,-3)\)。圖形就如圖二所示，這也再次說明切線不一定與圖形只相交於一點。

圖二

綜合上述，本文想要說明：利用微積分的術語和概念，能清楚定義什麼是切線，並且求切線斜率就是求導數，這使得「過圖形上一點求切線方程式」的問題成為微分的簡單應用，有著標準的解決方案。