微積分的dx(二)：從級數到函數論

微積分的dx(二)：從級數到函數論
李龍欣

上回我們簡單介紹了「無限小」的概念，而這回我們將時光倒流，看看在微積分剛剛發明後的大約100年期間的樣貌，以及這100年之後催生出的「極限」的概念，以及於此同時，質疑「函數」的思潮。

●十七、十八世紀的微積分

17世紀中期微積分發明之後，有許多未解的問題得到重大突破。例如在幾何方面，本來只能處理二次曲線的問題，但微積分用在其他曲線也有用。在處理過這些問題後，有很多曲線都可以寫成幂級數 (power series)──簡單來說就是把多項式變成無限多項。例如：

\(\tan^{-1}(x)=x-\frac{1}{3}x^3+\frac{1}{5}x^5-\frac{1}{7}x^7+\cdots\)

\(\cos(x)=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+\cdots\)

牛頓在分類三次曲線時尚須借助微積分，微積分又能處理無限多項的多項式，多麼振奮人心啊！也難怪 布魯克·泰勒(Brook Taylor，1685─1731) 會想要把所有函數都變成幂級數，而這個幂級數稱為泰勒展開式 (Taylor expansion)：

\(f(x)=\frac{1}{0!}f(a)+\frac{1}{1!}\frac{df}{dx}(a)(x-a)+\frac{1}{2!}\frac{d^2f}{dx^2}(a)(x-a)^2+\frac{1}{3!}\frac{d^3f}{dx^3}(a)(x-a)^3+\cdots\)

順帶一提，列翁哈特·歐拉(Leonhard Euler，1707─1783) 對於無限多個數相加這件事有獨到的見解。幂級數在他手中能有千變萬化，甚至能夠因式分解。

可是幂級數並沒有那麼美好。例如我們知道等比級數的公式

\(1+r+r^2+\cdots=\frac{1}{1-r}\)

歐拉注意到以下的推論 (分別代入 \(r=n\) 和 \(r=1/n\)) 不合理：

\((\cdots+\frac{1}{n^2}+\frac{1}{n}+1+n+n^2+\cdots)=-1+(1+n+n^2+\cdots)+(1+\frac{1}{n}+\frac{1}{n^2}+\cdots)\)

\(=-1+\frac{1}{1-n}+\frac{1}{1-\frac{1}{n}}=0\)

桂斗·格然迪(Guido Grandi，1671─1742) 也注意到在等比級數中代入 \(r=-1\) 的話會得到

\(\frac{1}{2}=(1-1+1-1+\cdots)=((1-1)+(1-1)+\cdots)=(0+0+\cdots)=0\)

這幾個例子都顯示出我們要更嚴肅地看待函數的運算。

●極限 (limit)

我們對於有限小的數做為分母、有限多個數相加都沒有問題，可是無限小的數做為分母、無限多個數相加本來就大有問題。時間回到18世紀的英國，詹姆士·朱林(James Jurin，1684─1750) 和 班哲明·羅賓斯(Benjamin Robins，1707─1751) 為首的兩派學者基於牛頓所提出的「極限」(limit) 的雛形展開筆戰，或許有影響到後人。歐陸方面，冉勒宏·達朗貝爾(Jean-le-Rond d’Alembert，1717─1783) 運用「極限」重新詮釋微分。譬如曲線 \(y=f(x)\) 上有兩個點 \((x,f(x))\) 和 \((x+\Delta x,f(x+\Delta x))\)，將兩點連起來得到的直線稱為割線 (secant line)。當 \(\Delta x\) 越小，這條直線就越接近 \((x,f(x))\) 的切線 (tangent line)，而割線的斜率也往切線的斜率靠近，而切線的斜率就是微分。

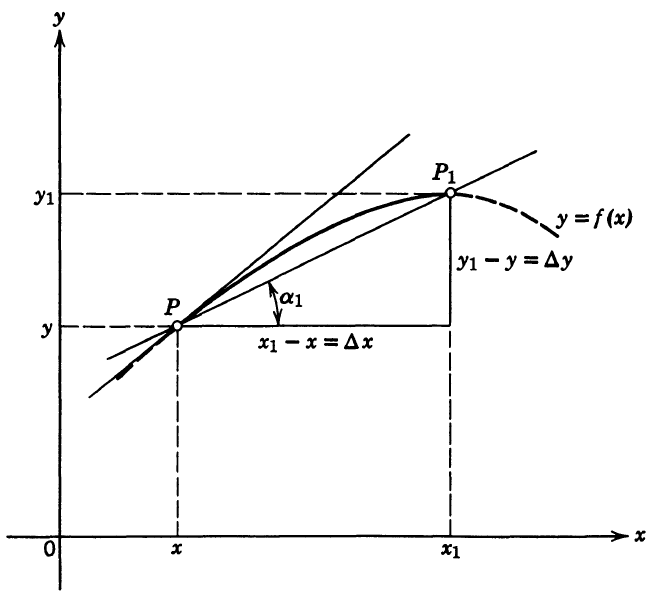
圖1：割線與切線。圖片來源：《Introduction to Calculus and Analysis》。R. Courant、F. John 著。初版(1989)。Springer-Verlag 出版(紐約/柏林/海德堡)

從有限小的 \(\Delta x\) 模擬無限小的 \(dx\)，這就是「極限」。從算式中可以看出其對應關係：

\(\displaystyle\frac{df}{dx}=\lim\frac{\Delta f}{\Delta x}\)

來到了19世紀，奧古斯丁·柯西(Augustin Cauchy，1789─1857) 進一步詮釋，為了方便應用到證明中，在敘述時需要先假設我們知道割線的斜率靠近的是哪個數，再把這個數稱為割線斜率的極限。達朗貝爾、柯西用文字描述極限而有點拗口，後來 卡爾·外爾許特拉斯(Karl Weierstraß，1815─1897) 發明的「\(\varepsilon-\delta\)語言」敘述起來更精簡但精神相同。

至於積分方面，回到原本的方法，用長方形面積來估計圖形的面積。長方形的寬度為  \(\Delta x\)^註1，高度和每一小段曲線的左端一樣高，如下圖所示：

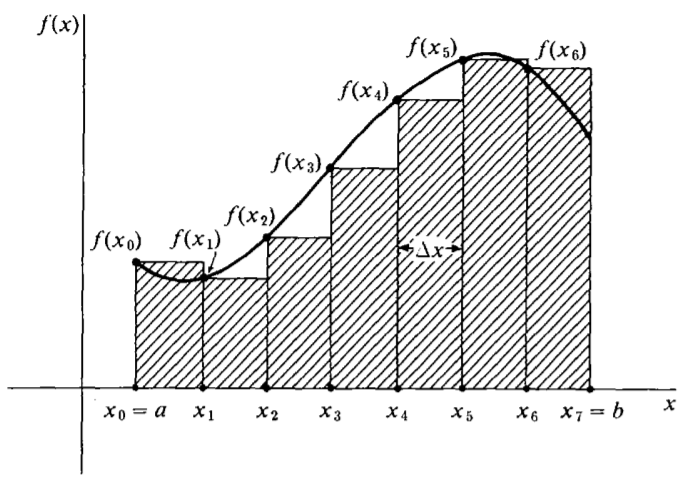
圖片來源：《Elementary Calculus: An Infinitesimal Approach》。H. Keisler 著。2019年9月修訂版。於網路免費公開。網址：http://www.math.wisc.edu/~keisler/calc.html。另有印刷版：第三版(2012)。Dover 出版(紐約)。

當 \(\Delta x\) 有限小、長方形有限多時的面積和稱為黎曼和 (Riemann sum)。當切割越來越細時，黎曼和的極限就是曲線下的面積。可以用算式表達為：

\(\displaystyle \int f(x)dx=\lim\sum f(x_i)\Delta x\)

同樣是用有限小的 \(\Delta x\) 模擬無限小的 \(dx\)。

●函數論 (theory of functions)

函數的意義從18世紀到19世紀經歷一大轉變。原本的函數所象徵的是「計算方法」，必需要是「可以算的」。後來發現函數能否計算、甚至是能否描述出來，似乎跟能否做微積分沒什麼關係了。因而需要針對能否做微積分的部分重新審視。例如下列兩個問題：

一、無窮和是否真的是數？哪些函數是幂級數？

為何要問這個問題？因為柯西發現一個泰勒展開式為 0 但原函數不是 0 的函數：

\(\displaystyle f(x)=\left\{\begin{array}{c} e^{-x^2} & \text{若}~x\neq 0 \\ 0 & \text{若}~x= 0\end{array}\right.\)

所以這個函數不是一個幂級數。

以一個幂級數

\(f(x)=A+B(x-a)+C(x-a)^2+D(x-a)^3+\cdots\)

來說，當 \(|x-a|\) 越小^註2，越有機會讓總和有限，而柯西也證明了確實如此。用柯西的根值檢驗法 (root test)，可以找到收斂半徑 (radius of convergence)。在 \(|x-a|\) 小於收斂半徑時都能當做函數並且用18世紀的方法做微積分。反之，在 \(|x-a|\) 等於收斂半徑時一定會在某些點遇到總和為無限大的問題。

二、什麼函數可以積分？

柯西首先用極限描述積分之後，貝恩哈特·黎曼(Bernhard Riemann，1826─1866) 認為並沒有理由要用左端點，而改成用曲線上任一點，並且只有當任意取法都得到同一個極限時才算是可以積分。接下來又進一步試圖改進的有很多，主要有：昂里·勒貝格(Henri Lebesgue，1875─1941)、托馬斯·斯提爾切斯(Thomas Stieltjes，1856─1894)、約翰·拉董(Johann Radon，1887─1956)。各個理論的「能夠積分」的函數各自略有不同。

而這兩個問題也分別成為複變分析 (complex analysis)、實變分析 (real analysis) 的開端。

註解:

[1]在柯西和黎曼的定義中，長方形的寬度不必相等，但是必須在取極限時全部縮小至 0。
[2]兩直劃的記號為複數的絕對值。

 參考資料：

1. 《A History of Mathematics》。F. Cajori 著。第二版(1961)。Macmillan 出版(紐約)。
2. 《A History of Mathematics》。U. Merzbach、C. Boyer 著。第三版(2011)。Wiley 出版(紐澤西)。
3. 《The Calculus Gallery: Masterpieces from Newton to Lebesgue》。W. Dunham 著。初版(2005)。Princeton University Press 出版(紐澤西)。
4. 〈Newton and Infinite Series〉。大英百科全書。於網路公開。網址：https://www.britannica.com/topic/Newton-and-Infinite-Series-1368282