轉動與平移運動的對照

轉動與平移運動的對照 (The Comparisons Between Motion and Rotational Motion)
天主教曉明女子高級中學物理科李忠義老師/國立臺灣師範大學物理系蔡志申教授責任編輯

在等角加速度運動公式的推導中，我們發現結果與一維等加速度運動有相似的對應：

因此我們進一步思考：牛頓力學在平移與轉動之間是否也可以對應？為此我們重新檢視牛頓第二定律：物體有加速度是因為受到外力 \(F\) 作用，有角加速度則是因為受到外力矩 \(\tau\) 作用。在牛頓 \(F=ma\) 中，\(m\) 為質量，質量越大則物體『維持原來習慣』的傾向越大（相同 \(F\) 作用，所得的加速度 \(a\) 越小），所以 \(m\) 更貼切的稱呼應為『慣量（inertia）』。同樣道理對應於轉動：當剛體受到相同 \(\tau\) 作用時，什麼物理量可用來表示『轉動的慣量』？亦即什麼物理量越大，所得的角加速度 \(\alpha\) 越小？

我們舉一簡單例子分析：一質點 \(m\) 受到外力作用繞參考點 \(O\) 轉動。

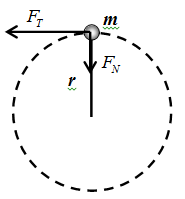
若將外力分成切線分力 \(F_T\) 與法線分力 \(F_N\)，則：

力矩 \(\tau=F_T\cdot r\)，其中 \(F_T=m\cdot a_T=m\cdot r\alpha\)

\(\therefore \tau = (m\cdot r\alpha)\cdot r=(mr^2)\cdot \alpha \stackrel{\text{對照}}{\longleftrightarrow} F=ma\)

兩者對照下可發現，轉動時物理量 \(mr^2\) 相當於平移運動中的慣量 \(m\)，亦即相同力矩 \(\tau\) 作用下，\(mr^2\) 越大者，獲得的角加速度 \(\alpha\) 越小，物體維持原來轉動狀態的趨勢越明顯，因此我們定義 \(I=mr^2\) 為質點的轉動慣量（Rotational Inertia）。

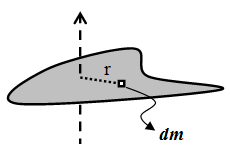
若物體為一具有體積的剛體，則轉動慣量以積分方式表示：\(I=\sum_im_ir^2_i=\int r^2dm\)

而根據上述推導，我們可以將力矩寫成：\(\vec{\tau}=I\vec{\alpha}=\vec{r}\times\vec{F}\)

接著我們進一步思考，牛頓定義動量 \(P\)，並用它來形容物體的運動狀態，若 \(P\) 發生改變則表示物體受到外力：\(\displaystyle F=\lim_{\Delta t\to \infty}\frac{\Delta P}{\Delta t}\)

而在轉動方面，是否同樣可以定義一個物理量來形容物體的『轉動狀態』？只要此物理量改變便可表示物體受到力矩 \(\tau\)？因此我們推導如下：

由 \(\displaystyle \tau = I\alpha = I\cdot \frac{\Delta\omega}{\Delta t}=\frac{\Delta(I\omega)}{\Delta t}\) 可知，『\(I\omega\)』若隨時變，即表示物體受到 \(\tau\)

另外由 \(\displaystyle \tau=Fr\sin\theta=r\sin\theta\cdot\frac{\Delta P}{\Delta t}=\frac{\Delta(rP\sin\theta)}{\Delta t}\) 亦可知，『\(rP\sin\theta\)』有相同效果

因此我們定義角動量（Angular Momentum）\(L=I\omega=rP\sin\theta\)，並將它用來表示物體轉動的運動狀態，只要角動量 \(L\) 隨時間發生改變，就表示物體受到外力矩。考量方向後我們將角動量寫成：\(\vec{L}=I\vec{\omega}=\vec{r}\times\vec{P}\)

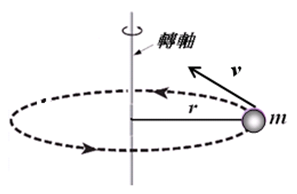
如圖，質點 \(m\) 繞定軸轉動，旋轉半徑為 \(r\)，速率為 \(v\)，則物體所具有的動能：\(E_K=\frac{1}{2}mv^2\)
若以轉動的角度分析，則相對於轉軸而言：\(E_K=\frac{1}{2}mv^2=\frac{1}{2}m(r\omega)^2=\frac{1}{2}(mr^2)\omega^2=\frac{1}{2}I\omega^2\)

上述的分析方式，常用於當質點系統有轉動的運動行為時，如滾動。此時若取系統的質心為轉動的參考點，則系統的總動能可表示成：總動能＝質心移動動能＋轉動動能。此種運用到相對運動概念的分析方式，在質點系統總動能也出現過：總動能＝質心動能＋內動能。兩者比較可發現，我們只是把內動能改以轉動的模式表示，基本的概念是相通的。

而作功方面，平移運動中外力作功：\(W=\vec{F}\cdot\vec{S}=(\text{外力沿位移方向的分力})\times(\text{位移})\)。若改以轉動分析，則切線方向分力所作的功可表為 \(W=\vec{F}\cdot \vec{S}=F_T\cdot(r\cdot \theta)=(F_T\cdot r)\cdot \theta=\tau\theta\)

同理可推功率為 \(P=\tau\omega\)

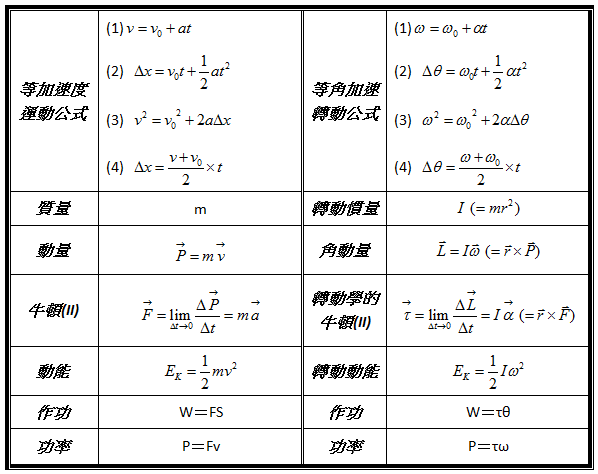
綜合以上所述，移動與轉動我們可以得到如下的對應：

參考資料：

1. 維基百科–旋轉動能  http://en.wikipedia.org/wiki/Rotational_energy