平面等加速度運動解題方法

平面等加速度運動解題方法
國立苑裡高級中學物理科許家銘老師/國立彰化師範大學物理系洪連輝教授責任編輯

一般而言，當我們處理平面等加速度運動時，會將所處理的座標分為兩個相互垂直的方向，（如：水平方向與鉛直方向、平行斜面方向與垂直斜面方向、切線方向與法線方向…等）在各自的方向上以直線運動的概念解題，在依其需要合併即得解，今天考慮平面向量及正弦定理，部分題型可以不須分解即可求解，通用例題如下：

例題：
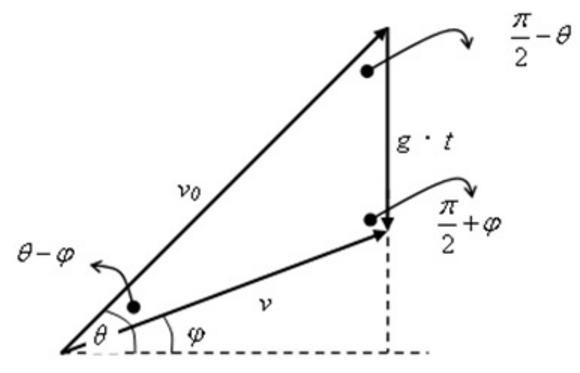
某物體自地面（或離地高 $$h$$）以初速度 $$v_0$$ 與水平夾 $$\theta$$ 角斜向拋出，在出發後時刻 $$t$$ 時，物體的速度為 $$v$$ 且與水平方向夾角 $$\varphi$$：

1.  物體的速度 $$v$$ ：
由加速度的定義：

$$\vec{a}=\displaystyle\frac{\Delta\vec{v}}{\Delta t}$$

$$\Delta \vec{v}=\vec{v}-\vec{v_0}=\vec{a}\cdot\Delta t$$

$$\vec{v}=\vec{v_0}+\vec{a}\cdot\Delta t$$

由正弦定理可得：

$$\displaystyle\frac{v_0}{\sin\left(\frac{\pi}{2}+\varphi\right)}=\frac{v_0}{\sin\left(\frac{\pi}{2}-\theta\right)}=\frac{gt}{\sin(\theta-\varphi)}$$

再依照所需求解 $$v$$ 或 $$t$$。如下例題：

問：
某物體自地面以仰角 $$60^\circ$$ 初速 $$20~m/s$$ 斜面拋出，經歷時間 $$t$$ 後，速度方向與水平方向夾俯角 $$30^\circ$$，試求：(1) $$v$$ 的大小 (2) $$t$$的大小 （$$g = 10~m/s^2$$）
答：
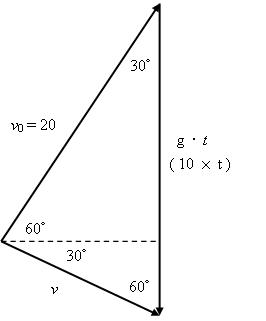
由角度關係及各物裡量方向，可繪出以下關係圖

由正弦定理可知

$$\displaystyle\frac{20}{\sin 60^\circ}=\frac{10\cdot t}{\sin 90^\circ}=\frac{v}{\sin 30^\circ}$$

1. $$\displaystyle v=\frac{20}{\sin60^\circ}\cdot\sin 30^\circ=\frac{20}{\sqrt{3}}=\frac{20\sqrt{3}}{3}~(m/s)$$
2. $$\displaystyle 10\cdot t=\frac{20}{\sin 60^\circ}\cdot \sin 90^\circ\Rightarrow{t}=\frac{2}{\sqrt{3}/2}=\frac{4}{\sqrt{3}}=\frac{4\sqrt{3}}{3}~(s)$$

2. 物體的位移 $$\Delta r$$：

由加速度的定義可得 $$\vec{v}=\vec{v_0}+\vec{a}t$$（取出發時時刻為零，出發點為原點），再由速度與位移的關係可得：

$$\displaystyle \vec{v}=\frac{d\vec{r}}{dt}=\vec{v_0}+\vec{a}\cdot t$$

$$d\vec{r}=(\vec{v_0}+\vec{a}\cdot t)dt$$

$$\int d\vec{r}=\int\limits^t_0(\vec{v_0}+\vec{a}\cdot t)dt$$

$$\vec{S}=\Delta \vec{r}=(\vec{v_0}\cdot t)+(\frac{1}{2}\vec{a}\cdot t^2)$$

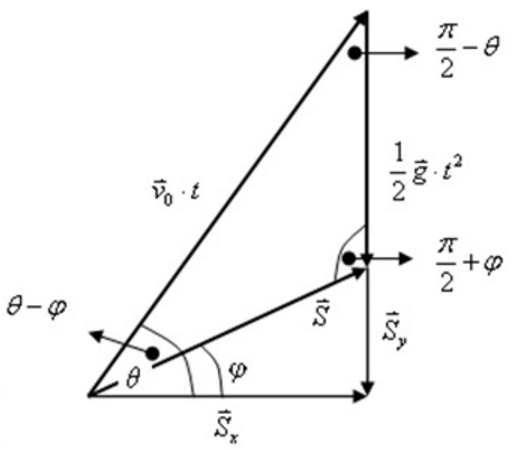
可得物體所做的位移可以區分為 $$(\vec{v_0}\cdot t)$$ 向量與 $$(\frac{1}{2}\vec{a}\cdot t^2)$$ 向量的合成，如圖

再由正弦定理求解相關物理量：

$$\displaystyle\frac{v_0\cdot t}{\sin(\frac{\pi}{2}+\varphi)}=\frac{S}{\sin(\frac{\pi}{2}-\theta)}=\frac{(\frac{1}{2}g\cdot t^2)}{\sin(\theta-\varphi)}$$

此一解法適用於求解斜面上的拋體運動，特舉一例題如下：

問：
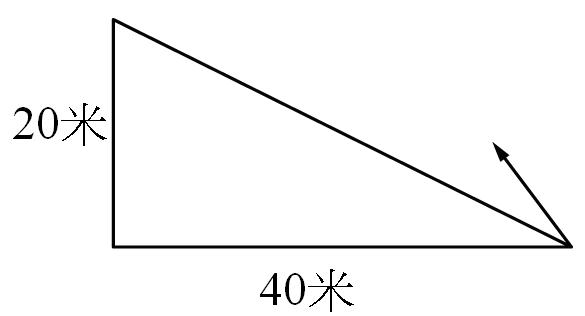
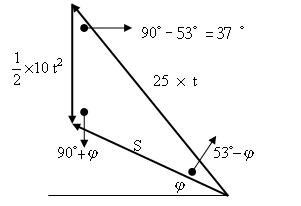
如圖，球在高度為 $$20$$ 米，寬度為 $$40$$ 米之坡底，以初速 $$25$$ 米／秒，與水平夾 $$53^\circ$$ 仰角丟出，則

(1) 物體於出發後何時落於斜坡面？
(2) 物體於斜面上的落點與出發點的距離？

答：

由正弦定理可得：$$\displaystyle\frac{25\cdot t}{\sin(90^\circ+\varphi)}=\frac{\frac{1}{2}\times{10}t^2}{\sin(53^\circ-\varphi)}=\frac{S}{\sin 37^\circ}$$

$$(1)$$ 由 $$\displaystyle\frac{25\cdot t}{\sin(90^\circ+\varphi)}=\frac{\frac{1}{2}\cdot 10t^2}{\sin(53^\circ-\varphi)}$$，化簡可得

$$\displaystyle\frac{5}{\cos\varphi}=\frac{t}{\sin(53^\circ-\varphi)}$$，其中 $$\displaystyle\cos\varphi=\frac{2}{\sqrt{5}},~~\sin\varphi=\frac{1}{\sqrt{5}},~~\tan\varphi=\frac{1}{2}$$

$$\displaystyle t=\frac{5\cdot(\sin(53^\circ-\varphi))}{\cos\varphi}=\frac{5(\sin53^\circ\cos\varphi-\cos53^\circ\sin\varphi)}{\cos\varphi}$$

$$\displaystyle t=5(\sin53^\circ-\cos53^\circ\tan\varphi)=5\left(\frac{4}{5}-\frac{3}{5}\times\frac{1}{2}\right)=2.5~(S)$$

$$(2)$$ 由 $$\displaystyle\frac{25\cdot t}{\sin(90^\circ+\varphi)}=\frac{S}{\sin 37^\circ}$$，化簡可得

$$\displaystyle S=\frac{25\cdot t}{\cos\varphi}\cdot\sin 37^\circ=25\times 2.5\times \frac{\sqrt{5}}{2}\times \frac{3}{5}=\frac{75\sqrt{5}}{4}~(m)$$

參考資料：
1.        南一版物理(上)教師手冊
2.        例題取材：翰林版題庫系統