認識擺線

Posted on 2011/09/11 in 幾何, 數學 with 沒有迴響 10,519 views

認識擺線 (On the Cycloid)
國立臺灣師範大學數系趙文敏教授/國立臺灣師範大學數系趙文敏教授責任編輯

摘要：在圓錐曲線發現之後，受到科學家們最多關注的曲線應該算是擺線了，它曾經引起許多科學家的競爭與爭吵，有人甚至把它比喻成古希臘時代特洛依戰爭中的海倫，本文介紹擺線的歷史與一些性質。

何謂擺線

在夜晚的路上，當一輛腳踏車從你面前疾馳而過時，如果車輪上掛著一個小燈泡，你可曾注意到小燈泡在前進過程中描繪出什麼樣的線條？

腳踏車在路上前進，車輪像一個圓，前進的路在一直線上，所以，腳踏車的前進可看成是一個圓在一直線上作沒有滑動的滾動。當一圖形在一曲線上作沒有滑動的滾動時，圖形上的每一個點在滾動過程中﹐都會描繪出一條曲線，這種曲線稱為「旋輪線」(roulette)。選擇不同的圖形、不同的曲線與不同的點，可以得出許多不同的旋輪線，我們舉出幾個例子如下。

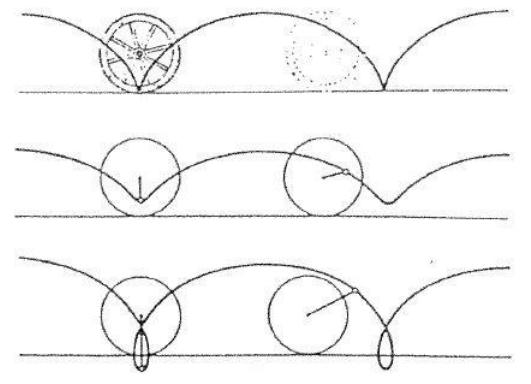
當一圓在一直線上作不滑的滾動時，在圓周上的點所描繪的旋輪線稱為「擺線」(cycloid)；在圓內部的點所描繪的旋輪線稱為短擺線(curtate cycloid)；在圓外部的點所描繪的旋輪線稱為長擺線(prolate cycloid)。短擺線與長擺線合稱為次擺線(trochoid)（參看圖一）。在下文中，我們將圓稱為滾動圓、直線稱為底線。擺線與底線相交的點是擺線的尖點(cusp)，兩相鄰尖點間的一段弧稱為擺線的一拱(arch)。

圖一

擺線的等時性質

在力學上，擺線具有很重要的性質，我們首先介紹它的等時性質（tautochrone property）。

將擺線的一拱倒轉，亦即：對其底線作鏡射，則此段擺線的最高點 \(C\) 變成最低點。此時，若一質點從此段擺線上任意點出發，在重力作用下沿擺線向下滑，則此質點到達最低點 \(C\) 所需的時間與出發點的位置無關，亦即：從任意兩相異點出發，它們到達 \(C\) 點的時間相同。這就是擺線的等時性質。

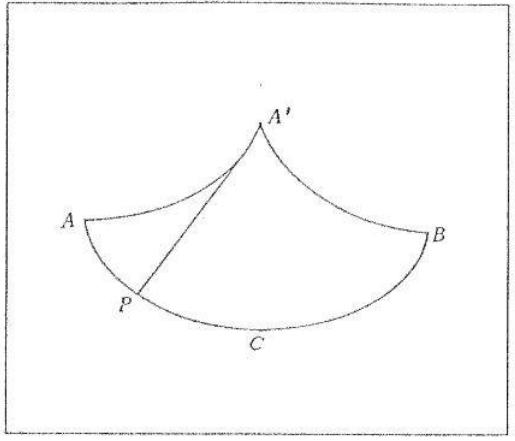
在圖二中，弧 \(ACB\) 是由擺線的一拱倒置而成、弧 \(AA’B\) 則是由同一擺線相鄰兩拱的中點間的一段倒置而成。若我們以一條長度為擺線一拱長之半的線繫住一個擺錘，另一端固定在弧 \(AA’B\) 的中點 \(A’\)。當擺錘擺動時，線的上端固定在點 \(A’\) 上，而下端有一段拉直。由於線長等於擺線一拱長的一半，擺錘擺動的路線就是圖二中的擺線弧。

前段所提的等時性，則是表示：不論振幅為何，其週期是個定值，此定值等於 \(2\pi\sqrt{(4a/g)}\)，其中 \(a\) 是擺線的滾動圓半徑，\(g\) 是重力加速度。

圖二

前段所提的裝置，稱為擺線鐘（cycloidal pendulum），這是 Christiaan Huygens（1629～1695年，荷蘭人）在 1673 年所發明的，它是具有真正等時性的鐘擺。

擺線的最速降性質

擺線在力學上的另一項重要性質，乃是最速降性質（brachistochrone property），我們說明如下。

若一質點在重力作用下，由 \(P\) 點沿著某曲線滑落到較低的 \(Q\) 點，設 \(P\) 與 \(Q\) 不在同一鉛垂直線上，則當滑行的曲線是以 \(P\) 點為尖點的一段倒轉的擺線弧時，質點由 \(P\) 點滑落到 \(Q\) 點所需的時間為最短。這就是擺線的最速降性質。

設 \(P\) 與 \(Q\) 的坐標分別是 \(P(x_1,y_1)\) 與 \(Q(x_2,y_2)\)，\(x_1<x_2\) 且 \(y_1>y_2\)，而 \(y=f(x)\) 是滿足 \(y_1=f(x_1)\) 與 \(y_2=f(x_2)\) 的一個函數，則一質點沿著曲線 \(y=f(x)\)，由 \(P\) 點滑落到 \(Q\) 點所需的時間，可以表示成某個由 \(f(x)\) 與 \(f'(x)\) 組成的函數的定積分。

在所有此種函數 \((y=f(x))\) 中，那一個函數能使此定積分的值最小，這個問題乃是「一個以函數（或曲線）為變數的極值問題」。研究這類問題的方法稱為「變分學」（calculus of variation）。它與微積分中討論極值的方法不相同，而且也困難得多。探討最速降曲線的問題，乃是變分學的先驅問題之一，一般的變分學書籍都會談到這個例子。

在最速降曲線問題中，有一個問題必須交待，那就是：對任意二點 \(P(x_1,y_1)\) 與 \(Q(x_2,y_2)\)，\(x_1<x_2\) 且 \(y_1>y_2\)，有多少擺線以 \(P\) 點為一尖點而又通過 \(Q\) 呢？答案是：恰有一條。

給了 \(P\)、\(Q\) 兩點，我們怎麼作出這樣的擺線呢？任取一圓，使它與過點 \(P\) 的水平直線切於 \(P\) 點且圓在水平直線下方。讓圓在水平直線下滾動，設定點 \(P\) 的軌跡與直線 \(PQ\) 交於 \(Q’\) 點。另取一圓，其半徑等於前一圓的半徑乘以 \(\frac{\overline{pq}}{\overline{PQ’}}\)，則將後一圓在過 \(P\) 點的水平直線下滾動時，定點 \(P\) 所描繪的軌跡，就是以 \(P\) 為一尖點且通過 \(Q\) 的擺線。

前段所提的作法，事實上與擺線的一項性質有關。若兩擺線的底線重合，且有一尖點重合，則其中任一擺線都可由另一擺線以重合尖點為中心，放大或縮小而得。換言之，任意二擺線都是相似的曲線。

擺線史話

在圓錐曲線發現之後，受到科學家們最多關注的曲線應該算是擺線了，它曾經引起許多科學家的競爭與爭吵，有人甚至把它比喻成古希臘時代特洛依戰爭中的海倫，而稱之為「the Helen of geometry」。

伽利略（Galileo，1564～1642年，義大利人）是最早注意到擺線的科學家之一，他在 1599 年曾經嘗試以操作的方法，來計算擺線的一拱與其底線間的面積。他將輪子在一直線上滾動，實地描繪出擺線的一拱，然後利用相同的材料做成擺線的一拱以及滾動圓，在天平上秤的結果發現擺線的一拱與三個滾動圓盤大致平衡。所以，擺線一拱的面積大約是滾動圓面積的三倍，這是正確的。不過，伽利略卻覺得比值應該是無理數，所以，他猜測擺線一拱的面積是滾動圓面積的 \(\pi\) 倍。

擺線一拱的面積，是 Gilles Persone de Roberval (1602～1675年，法國人）在 1634 年最先求得的。他在 1638 年還找到擺線之切線的作法。約在同一時期，笛卡兒（Descartes，1596～1650年，法國人）與費瑪（Fermat，1601～1665年，法國人）也找到切線的作法。另外，Roberval 也討論過擺線的一拱繞其底線旋轉所得旋轉體的體積。

就在 Roberval 研究擺線有所成就的時候，伽利略的一位學生 Torricelli（1608～1647 年，義大利人）也對擺線大感興趣。1643 年，Torricelli 出版一篇名為〈De parabole〉的作品，其中附帶提到擺線的求積法與切線的作法，但卻沒有提到 Roberval 在他之前已經得出這兩個結果。由於這個緣故，Roberval 曾在 1646 年寫信譴責 Torricelli 竊取他人的研究成果。對於這件事，後世數學史家認為 Torricelli 是受冤枉了，因為 Roberval 的成果直到 1693年才發表。

1658 年，曾經在四年前就放棄數學轉攻神學的天才數學家巴斯卡（Pascal， 1623～1662 年，法國人）發生一件趣事。有天晚上，巴斯卡因牙痛而睡不著覺，為了想忘掉疼痛，就專心思考擺線的性質。想著想著，牙齒竟然不痛了，巴斯卡認為這是上帝在給他提示，表示他研究數學並沒有惹上帝不高興。

於是，他全心投入來探討擺線的性質，數天後，他就獲得一些與擺線有關的面積、體積與重心等方面的結果。他將研究所得寫成問題向當代數學家提出挑戰，並且設置兩個獎，還請 Roberval 擔任其中的一位評審人。也許因為沒能公告給多數人知道，或是因為時間太緊迫了，這次懸賞行動只收到 Antoine de Lalouvire(1600～1664年，法國人)與 Wallis(1616～1703年，英國人）的回應，而且所送的解答中還有一些計算上的錯誤，所以，巴斯卡沒有頒獎，只將他自己的研究成果寫成〈Histoire de la roulette〉一文予以發表。（當時的法國人將擺線稱為 roulette。）結果呢？與賽的兩人因為沒有頒獎而不高興，而義大利的數學家們則為巴斯卡在〈擺線的歷史〉一文中沒有提到 Torricelli 而不痛快。

就在 Wallis 參加巴斯卡的挑戰的同時，另一位英國人 Wren （1632～1723年）﹐將他所得的擺線弧長的求法寄給巴斯卡，這是巴斯卡不曾得到的結果。Wren 後來轉行去研究物理與建築，1666 年倫敦大火後，Wren 就因為設計倫敦的聖保羅教堂而聞名。

擺線在力學方面的性質，等時性係 Huygens 所發現的，而最速降性質則是白努利（J.Bernoulli, 1654～1705年，瑞士人）在 1690 年發現的。

延伸閱讀