面膨脹係數

面膨脹係數 (coefficient of area expansion)
國立臺灣師範大學附屬高級中學物理科李柏翰老師

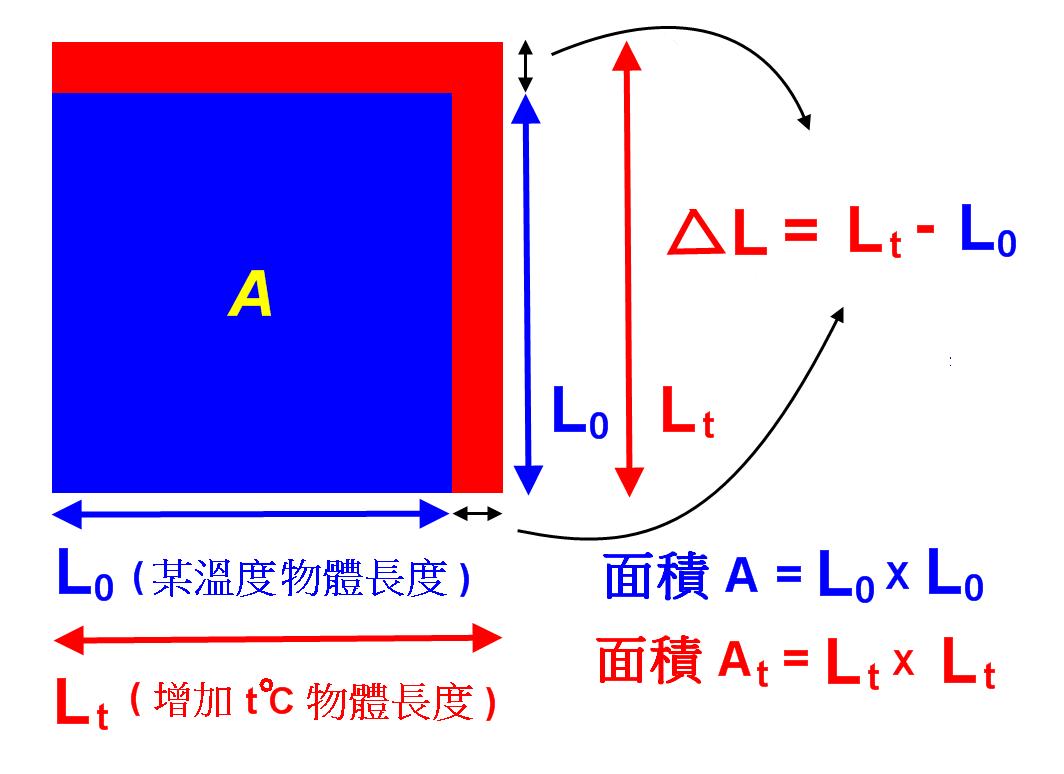
一般而言，當物質受熱時，本身在熱脹冷縮效應作用之下，其物質本身的幾何特性，例如長度、面積或者是體積會隨著溫度的變化而發生變化。如果溫差改變不大，則一維的物體之長度增加的百分比會和溫差成正比，其比例係數稱為線膨脹係數，而所謂面膨脹係數是指：溫度增高時，面積增加量的百分比會和溫差成正比，如下圖1所示。

圖1$$~~~$$考慮二維的物體在受熱時，因為每邊的長度發生變化，而導致面積變化量 $$\Delta A=A_t-A_0$$ (作者提供)

更具體說，所謂面膨脹係數 $$\beta$$，是指固體在溫度每改變攝氏 $$1$$ 度時，其面積的變化和它在原溫度時原面積的比值。

$$\displaystyle \beta=\frac{\Delta A}{A_o\cdot t}=\frac{A_t-A_0}{A_o\cdot t}\Rightarrow A_t=A_0(1+\beta t)$$

其中 $$L_0$$ 是指固體在原參考溫度時的長度，$$A_0$$ 是固體在原參考溫度時的面積，溫度的增加量，$$L_t$$ 是指增加了 $$t^\circ C$$ 時的長度，$$A_t$$ 是固體在增加了 $$t^\circ C$$ 時的面積，$$\beta$$ 則定義為面膨脹係數，$$(1/^\circ C)$$ 面膨脹係數 $$\beta$$ 約為線膨脹係數 $$\alpha$$ 的 $$2$$ 倍，即 $$\beta\approx 2\alpha$$ 其證明如下：

$$A_t=L_t\times L_t=L_0(1+\alpha t)\times L_0(1+\alpha t)$$

$$A_0=L_0^2$$

$$A_t=A_0(1+\alpha t)^2=A_0(1+2\alpha t+\alpha^2 t^2)\sim A_0(1+2\alpha t)$$

$$A_t=A_0(1+\beta t)$$

又因為線膨脹係數 $$\alpha$$ 很小，高次項可以忽略不計，所以 $$\beta=2\alpha$$，即面膨脹係數 $$\beta$$ 約為線膨脹係數 $$\alpha$$ 的 $$2$$ 倍。

體膨脹係數 coefficient of cubical expansion

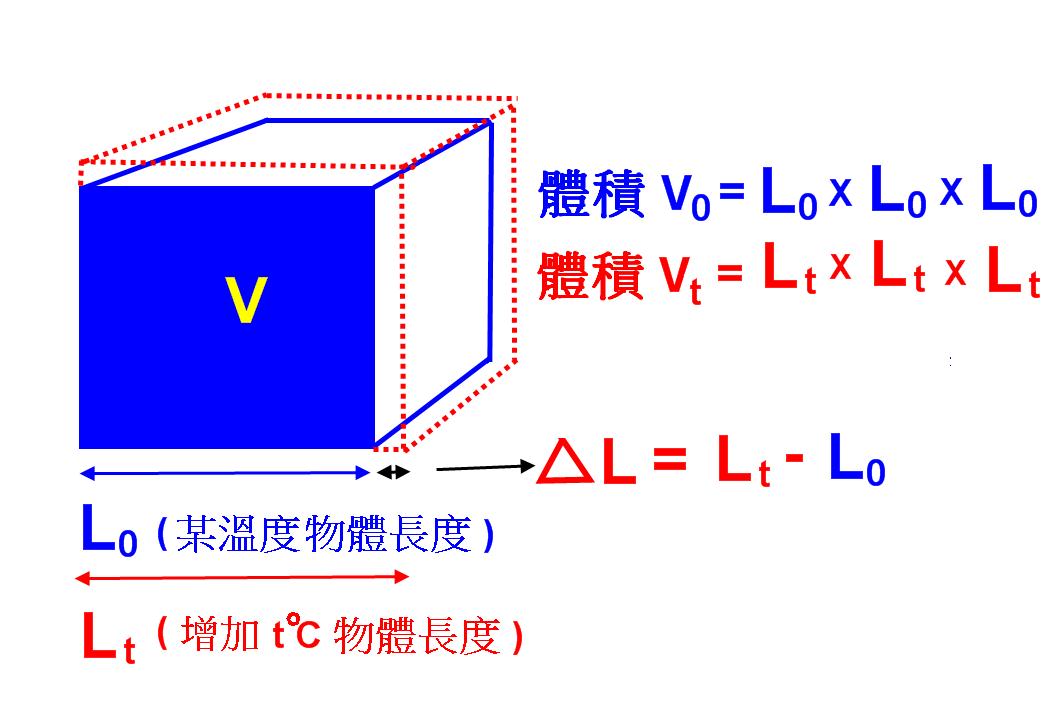
所謂體膨脹係數 $$\gamma$$ 是指：溫度增高時，體積增加量的百分比會和溫差成正比，也可以定義為固體在溫度每改變攝氏 $$1$$ 度時，其體積的變化和它在原溫度時原體積的比值，如下圖2所示。

$$\displaystyle \gamma=\frac{\Delta V}{V_0\cdot t}=\frac{V_t-V_0}{V_0\cdot t} \Rightarrow V_t=V_0(1+\gamma t)$$

圖2$$~~~$$考慮三維的物體在受熱時，因為每邊的長度發生變化，而導致體積變化量 $$\Delta V=V_t-V_0$$ (作者提供)

其中 $$V_t$$ 是固體在增加了 $$t^\circ C$$ 時的體積，$$\gamma$$ 則定義為體膨脹係數 $$(1/^\circ C)$$，體膨脹係數 $$\gamma$$ 約為線膨脹係數 $$\alpha$$ 的 $$3$$ 倍，即 $$\gamma=3\alpha$$，推導證明如下:

$$V_t=L_t\times L_t\times L_t=L_0(1+\alpha t)\times L_0(1+\alpha t)\times L_0(1+\alpha t)$$

$$V_0=L_0^3$$

$$V_t=V_0(1+\alpha t)^3=V_0(1+3\alpha t+3\alpha^2 t^2+t^3)\sim V_0(1+3\alpha t)$$

$$V_t=V_0(1+\gamma t)$$

又因為線膨脹係數 $$\alpha$$ 很小，高次項可以忽略不計，所以 $$\gamma=3\alpha$$，體膨脹係數 $$\gamma$$ 約為線膨脹係數 $$\alpha$$ 的 $$3$$ 倍。

須注意的是：在以上的討論中，我們都暗中假設物體所受的應力並未改變。如果物體受到外界的限制，使得其面積或體積無法完全自由膨脹或收縮，則面積或體積的增減百分比自然無法利用上述公式來描述。於此同時，物體內的應力也會改變，因此，如何計算出面積或體積的增減比例會更加複雜。