牛頓法 ( Newton’s Method )

牛頓法 ( Newton’s Method )
國立屏東高級中學數學科楊瓊茹老師

在2008年上映的美國電影《決勝21點》中，教授米奇 (Mickey Rosa) 請同學們解釋「牛頓法」及其應用，此時班 ( Ben Campbell ) 卻語出驚人說：「牛頓剽竊了拉福生的方法。」

站在巨人肩上的牛頓是剽竊者？這是真的嗎？

所謂的「牛頓法」( Newton’s Method ) 是指求解方程式 \(f(x)=0\) 的根之疊代法 (Iterative Method)，又稱為「牛頓–拉福生演算法」( Newton-Raphson Algorithm)。

設 \(f(x)\) 是可微分的函數，

令 \(s\) 為 \(f(x)=0\) 的根，

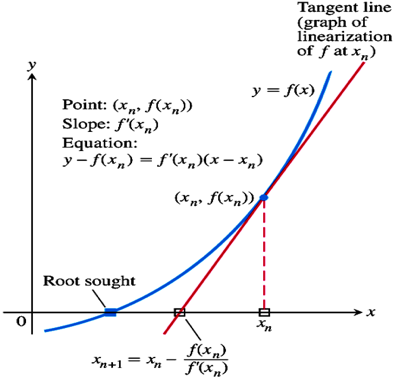
考慮切線 \(L:y-f(x_n)=f'(x_n)(x-x_n)\)

與 \(x\) 軸的交點 \((x_n-\frac{f(x_n)}{f'(x_n)},0)\) ，

當 \(x_n\) 很接近 \(s\)，

\(x_n-\frac{f(x_n)}{f'(x_n)}\) 比 \(x_n\) 更接近 \(S\) 。

故 \(x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\)

此一等式即為求解 \(f(x)=0\) 的「牛頓法」。

雖然「牛頓法」通常可以找出根 \(s\) 的近似值，但要注意其收斂性的罩門。
接著，我們分別檢視牛頓和拉福生的方法。
西元1669年夏天，
牛頓 ( Issac Newton, 1642-1727 ) 在劍橋寫下方程式 \(x^3-2x-5=0\) 的解法︰

假設 \(x^3-2x-5=0\) 是可解的︰並且令 \(2\) 小於所求的根，則取 \(2+p=x\) 

並且將它代入方程式，結果產生新的方程式 \({p^3} + 6{p^2} + 10p – 1 = 0\) ，

此根 \(p\) 為所尋求被加到商數的數︰

特別地 (當 \(p^3+6p^2\) 在說明為很小而被忽略時)

\(10p-1=0\) 或 \(p=0.1\) 是非常接近真正的值；

因此，我在商數的地方寫下 \(0.1\) 並且假設 \(0.1+q=p\) ，

將它代入 \({p^3} + 6{p^2} + 10p – 1 = 0\) ，

如同之前，產生 \({q^3} + 6.3{q^2} + 11.23q + 0.061 = 0\) 。

而且因為 \(11.23q + 0.0061[ = 0]\) 很接近實際的 \(q\) 或幾乎 \(q=-0.0054\)，

我在商數的最下面寫下 \(-0.0054\)。

同樣地，假設 \(-0.0054+r=q\) ，如同之前的方法代換，繼續運算到滿意為止。

拉福生 ( Joseph Raphson, 1648-1715 ) 在1690年所著作的《通用方程分析》(Analysis Aequationum Universalis) 中，給出解方程式  \(ba-a^3=c\) 的根 \(a\) 之方法︰

假設 \(g+z=a\)，

所以 \(bg – {g^3} + (b – 3{g^2})z – 3g{z^2} – {z^3} = ba – {a^3} = c\)，

因此 \((b – 3{g^2})z – 3g{z^2} – {z^3} = c + {g^3} – bg\) ，

\( + z – \frac{{3g{z^2} + {z^3}}}{{b – 3{g^2}}} = \frac{{c + {g^3} – bg}}{{b – 3{g^2}}} =+ x\) ，

由收斂定理，我們得到 \( + z =+ x + \frac{{3g{z^2} + {g^3}}}{{b – 3{g^2}}}\)，並且兩邊加上 \(g\)，

產生 \(g + z = a = g + x + \frac{{3g{z^2} + {z^3}}}{{b – 3{g^2}}}\)。

但是這新的 \(g=g+x\) 比先前的 \(g\) 增加了 \(x\)，比 \(a\) 少了 \(\frac{{3g{z^2} + {z^3}}}{{b – 3{g^2}}}\) ，證明完畢。

兩人所發表的方法有所不同。不過值得注意的是，拉福生亦是倫敦皇家學會的會員，在1690年代早期，曾在劍橋與牛頓接觸過，當時他是牛頓與萊布尼茲 ( Leibniz,1647-1716) 微積分優先權論戰的牛頓支持者。

至於牛頓獲得疊代法的桂冠是否實至名歸？其實，兩人的解法都沒有涉及微分的概念。雖然拉福生所導出新的 \(g\) 值 \(g + \frac{{c + {g^3} – bg}}{{b – 3{g^2}}}\) 與微分公式 \({x_{n + 1}} = {x_n} – \frac{{f({x_n})}}{{f'({x_n})}}\) 是相容的，但他並沒有洞察出這個公式。

直到1740年，數學家辛普森 ( Thomas Simpson, 1710-1761) 才使用微分的形式來操作。早期在十八世紀的數學家們總能小心區分牛頓與拉福生的方法，但法國數學家傅立葉 ( Joseph Fourier, 1768-1830 )在著作中，將使用微分符號的疊代法描述為「牛頓法」，在當時傅立葉的著作頗受好評，時至今日，我們也沿用「牛頓法」一詞。

參考資料

1. Fauvel, John (1998),“Algorithms in the Pre-calculus Classroom: Who was Newton- Raphson? ”, Mathematics in School 27: 45- 47.
2. N. Kollerstrom (1992), “Thomas Simpon and Newton’s Method of Approximation:an enduring myth”, British Journal of History of Science 25: 347-354.
3. Cajori, Florian (1911),“Historical Note on the Newton-Raphson Method of Approximation”,The American Mathematical Monthly 18: 29-32.
4. 「牛頓法」的圖形源自Thomas/Finney (1996),《Calculus》, Addison-Wesley Publishing Company.