二元一次不等式(Two-Variable Inequalities)

二元一次不等式(Two-Variable Inequalities)
臺北市立第一女子中學數學科蘇俊鴻老師

若 $$a,b,c$$ 為實數，且 $$a,b$$ 不同時為0，則稱 $$ax+by+c=0$$ 為二元一次方程式；

又因為它的圖形為一直線，也稱為直線方程式。

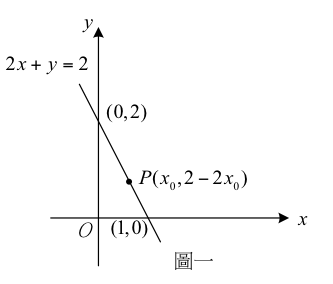
圖一正是二元一次方程式 $$2x+y=2$$ 的圖形。事實上，直線 $$2x+y=2$$ 上的任一點，

其坐標 $$(x,y)$$ 都滿足方程式 $$2x+y=2$$，換言之，都是方程式 $$2x+y=2$$ 的解。

因此，當點 $$P$$ 的 $$x$$ 坐標為 $$x_0$$ ，易推得 $$y$$ 坐標為 $$2-2x_0$$ 。

當我們將方程式其中的等號 $$”=”$$ 改成不等號 $$”>”,”\ge”,”<“$$ 或 $$”\le”$$ 就稱為二元一次不等式。

例如， $$2x+y>2,2x+y\le 2$$ 均為二元一次不等式。

然而，滿足二元一次不等式的解又會形成什麼圖形呢？

比如說，滿足 $$2x+y>2$$ 的解是什麼圖形？

仔細觀察圖二，直線 $$2x+y=2$$ 將平面分成二個半平面，成為兩個半平面的界線。

顯然，直線 $$2x+y=2$$ 上的點並不滿足 $$2x+y>2$$。

若在上半平面(斜線標示)內任取一點 $$Q(x_0,y_0)$$，

過 $$Q$$ 點作 $$x$$ 軸的垂線，交直線 $$2x+y=2$$ 於 $$P$$ 點，則 $$P$$ 點坐標為 $$(x_0,2-x_0)$$ 。

由於 $$Q$$ 點在 $$P$$ 點上方 $$\Rightarrow y_0>2-x_0 \Rightarrow 2x_0+y_0>2$$ ，

因此 $$Q(x_0,y_0)$$ 滿足 $$2x+y>2$$ ，

這也說明了上半平面(斜線標示)上的任一點都是 $$2x+y>2$$ 的解。

同理，下半平面上的任一點都是 $$2x+y<2$$ 的解。

一般而言，若不等式的解區域不含界線，會以虛線表示。

若是二元一次聯立不等式的解區域，則是將每一個二元一次不等式的解區域繪出，再取其交集。

如圖三，即為 $$\left\{ \begin{array}{l} 4x – y – 7 \le 0\\ 3x – 4y + 11 \ge 0\\ x + 3y – 5 \ge 0 \end{array} \right.$$ 的解區域。

進一步，在滿足聯立不等式的條件下，我們還能考慮所求函數的極值問題，

比如說， $$x,y$$ 滿足聯立不等式 $$\left\{ \begin{array}{l} 4x – y – 7 \le 0\\ 3x – 4y + 11 \ge 0\\ x + 3y – 5 \ge 0 \end{array} \right.$$ ，

求 $$f(x,y)=x-y$$ 的最大值與最小值。該如何處理？

這時幾何表徵成為很好的切入點，無論 $$x,y$$ 何值，代入 $$f(x,y)=x-y=k$$ 正是代表一條直線，而 $$k$$ 值的變動，即是一組斜率為 $$1$$ 的平行直線(如圖四)，因此，便可觀察到最大值發生在點 $$(2,1)$$ ，最大值為 $$1$$ ；最小值發生在點 $$(-1,2)$$ ，最小值為 $$-3$$。

將幾何表徵與代數式的連結，是數學解題重要的技巧，不妨再考慮這一題：

若 $$x,y$$ 承上述限制，求 $$g(x,y) = \frac{{y + 2}}{{x + 3}}$$ 的最大值與最小值。

建議想想直線斜率的定義，應該很快就能得到最大值為 $$2$$；最小值為 $$\frac{3}{5}$$。

其實，許多日常生活中的問題都能表示成二元一次聯立不等式，因此，上述滿足某些二元一次不等式的條件，找尋所求函數的最大或最小值的方法，成為我們解決實際問題，提出最佳解法的憑據。有興趣的讀者，請參閱〈線性規劃〉一文。