我們同一天生日（二）！（We have the same birthday!）

我們同一天生日（二）！（We have the same birthday!）
臺北市立和平高中黃俊瑋教師

連結：我們同一天生日（一）！（We have the same birthday!）

〈我們同一天生日（一）〉一文中討論了下述問題：某一群人數共有 \(n\) 人，其中有某 \(2\) 個人同一天生日的機率為何？特別地，當這群人的人數到達 \(23\) 人以上時，有某 \(2\) 個人同一天生日的機率將大於 \(1/2\)。

該文中利用反面作法，先計算 \(n\) 個人生日皆不同天的機率為：

\(\frac{{365}}{{365}} \times \frac{{364}}{{365}} \times \frac{{363}}{{365}} \times\cdots\times \frac{{365 – n + 1}}{{365}}\)。

因此，\(n\) 個人當中有某 \(2\) 個人同一天生日的機率為：

\(1 – \left( {\frac{{365}}{{365}} \times \frac{{364}}{{365}} \times \frac{{363}}{{365}} \times\cdots\times \frac{{365 – n + 1}}{{365}}} \right)\) 。

欲計算不同的 \(n\) 相對應的機率，除了可以利用計算機與電腦之外，我們還可以利用對數的概念與查表的方式，計算出上述各機率值。這裡先來看看人數為 \(4\) 個人時的例子。

首先，計算出四個人生日皆不同天的機率 \(\frac{{364}}{{365}} \cdot \frac{{363}}{{365}} \cdot \frac{{362}}{{365}}\)，這裡我們取常用對數：

\(\begin{array}{ll}\log (\frac{{364}}{{365}} \cdot \frac{{363}}{{365}} \cdot \frac{{362}}{{365}})&=\log 364+\log 363+\log 362-3\log 365 \\ &=\log (3.64 \cdot {10^2}) + \log (3.63 \cdot {10^2}) + \log (3.62 \cdot {10^2}) \\&~~~- 3 \cdot \log (3.65 \cdot {10^2})\\&=\log 3.64 + \log 3.63 + \log 3.62 – 3 \cdot \log 3.65\end{array}\)

接著，查對數表後可得：\(\log (\frac{{365}}{{365}} \cdot \frac{{364}}{{365}} \cdot \frac{{363}}{{365}} \cdot \frac{{362}}{{365}})\) 約等於

\(0.5611 + 0.5599 – 0.5587 – 3 \times 0.5623 =-0.0072=-1+0.9928\)

查對數表可知 \(\log 0.983 \approx – 1 + 0.9926\) 且 \(\log 0.984 \approx – 1 + 0.9930\)。

再利用內插法可估算此值約為 \(- 1 + 0.9928 \approx \log 0.9835\)，

即 \(\frac{{364}}{{365}} \cdot \frac{{363}}{{365}} \cdot \frac{{362}}{{365}}\) 約為 \(0.9835\)。

故四個人當中有某 \(2\) 個人同一天生日的機率為 \(1-0.9835=0.0165\)。

不過，當我們要計算 \(23\) 個人生日都不同天的機率時，查表未必比按計算機來得快或方便。

接下來，筆者再提供另一個估算的方法。

\(23\) 個人生日都不同天的機率為 \(\frac{{365}}{{365}} \times \frac{{364}}{{365}} \times \frac{{363}}{{365}} \times\cdots \times \frac{{343}}{{365}}\)。

將此式中的第 \(1\) 項與第 \(23\) 項配對、第 \(2\) 項與第 \(22\) 項配對、\(\cdots\)、第 \(k\) 項與第 \(24-k\) 項配對。

由於 \(365\times 343\)、\(364\times 344\)、\(\cdots\)、\(355\times 353\)

皆約略等於中間項（中位數）\(354\) 的平方，故原式約等於 \({(\frac{{354}}{{365}})^{23}}\) ，

這時取對數再查表可得：

\(\begin{array}{ll}\log {(\frac{{354}}{{365}})^{23}} &= 23\log \frac{{354}}{{365}} = 23(\log 354 – 365)\\&\approx 23(0.5490 – 0.5623)=23\times(-0.0133)=-0.3059=- 1 + 0.6941\\&\approx\log 0.4945\end{array}\)

故 \(23\) 人當中有二個人同一天生日的機率約為 \(1-0.4945=0.5055\) ，

此近似值與真正的機率值相去不遠。

類似地，當我們欲估算 \(n\) 個人當中有某 \(2\) 個人同一天生日的機率時，

需先估算出 \(\frac{{365}}{{365}} \times \frac{{364}}{{365}} \times \frac{{363}}{{365}} \times\cdots\times \frac{{365 – n + 1}}{{365}}\)，

此時，同樣將第 \(k\) 項與第 \(n+1-k\) 項依序作配對，可得下列近似關係：

\(\frac{{365}}{{365}} \times \frac{{365 – n + 1}}{{365}} \approx {(\frac{{365 – \frac{{n – 1}}{2}}}{{365}})^2}\)

\(\cdots\)

\(\frac{{365 – k}}{{365}} \times \frac{{365 – n + 1 + k}}{{365}} \approx {(\frac{{365 – \frac{{n – 1}}{2}}}{{365}})^2}\)

則 \(\log (\frac{{365}}{{365}} \times \frac{{364}}{{365}} \times \frac{{363}}{{365}}\times\cdots\times \frac{{365 – n + 1}}{{365}})\)

約等於 \(\log {(\frac{{365 – \frac{{n – 1}}{2}}}{{365}})^n} = n\log (\frac{{365 – \frac{{n – 1}}{2}}}{{365}})\)

無論 \(n\) 為奇數或偶數，上式亦成立。

此式相當於將第 \(k\) 項與第 \(n+1-k\) 項依序作配對，

再將第 \(k\) 項與第 \(n+1-k\) 項之乘積以這 \(n\) 個數之中位數的平方作近似。

這時，只需代入想要的 \(n\) 便可計算出相對應的近似值，

再反查表即可估算出下述 \(n\) 個人生日皆不同一天的機率：

\(\frac{{365}}{{365}} \times \frac{{364}}{{365}} \times \frac{{363}}{{365}} \times\cdots\times \frac{{365 – n + 1}}{{365}}\)，

進一步可估算出 \(n\) 個人當中有某 \(2\) 個人同一天生日的機率。

圖一 \(P(n)\( 之函數圖形

最後，我們試利用此式造一函數：\(P(n) = 1 – {10^{n\log (\frac{{365 – \frac{{n – 1}}{2}}}{{365}})}}\) 來估算機率值，

其中 \(P(n)\) 表示 \(n\) 個人當中有某 \(2\) 個人同一天生日的機率近似值。

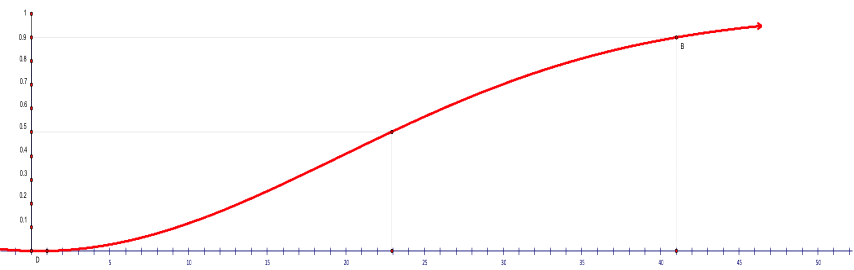
就此函數來看，只當 \(n\) 為正整數時有實值上的意義。圖一所示為此函數之圖形，橫座標為人數 \(n\)，縱坐標為 \(n\) 個人當中有某 \(2\) 個人同一天生日的機率近似值。從圖形可看出此函數的走勢，從虛線標示處亦可看出當人數為 \(23\) 人時，此機率約為 \(0.5\)，當人數為 \(41\) 人時，此機率為 \(0.9\)。當人數超過 \(50\) 之後，機率會非常接近 \(1\)。這也是為什麼當一個班級或一群人的人數超過 \(50\) 人後，幾乎可肯定有某兩人的生日落在同一天。