無母數統計—威爾卡森符號檢定

無母數統計—威爾卡森符號檢定(Non-parameter Statistics: Wilcoxon Signed-rank Test)
國立臺灣大學園藝暨景觀學系 李韶凱

一、前言

如果想檢測的資料無法直接假設其服從特定分布，應採用無母數 (nonparametric) 統計法進行檢定。本文將介紹檢驗單樣本的無母數方法—威爾卡森符號等級檢定 (Wilcoxon signed-rank test)。

二、威爾卡森符號檢定 (Wilcoxon signed-rank test)

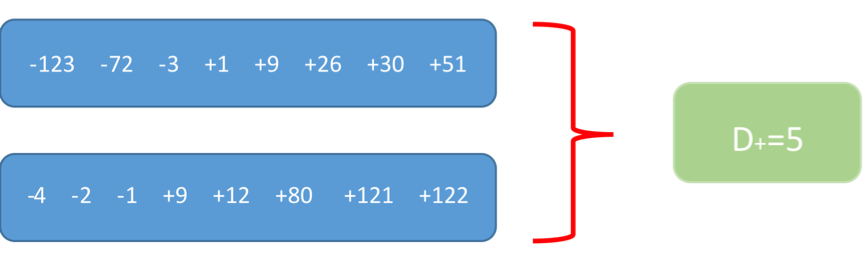
使用符號檢定  (sign test) 的檢定統計量（參考《無母數統計—符號檢定》一文）使用一組樣本，而且對於抽樣的所有觀測值只由正號或負號表示與中位數的關係，圖一的例子表示兩組比較的差異都是五個正號 (D = 5)，但是數值的差異卻被忽略了。換句話說，就是指考慮方向，而未考慮數值大小的統計方法。而威爾卡森符號檢定則加以修正，除了保留符號檢定的正負號外，也將觀測值數值大小的排序 (rank) 加入統計量的計算，因此檢定力 (power) 較符號檢定來得強。

圖一、兩組假設比較的資料在符號檢定下有同樣的結果。（本文作者李韶凱繪製）

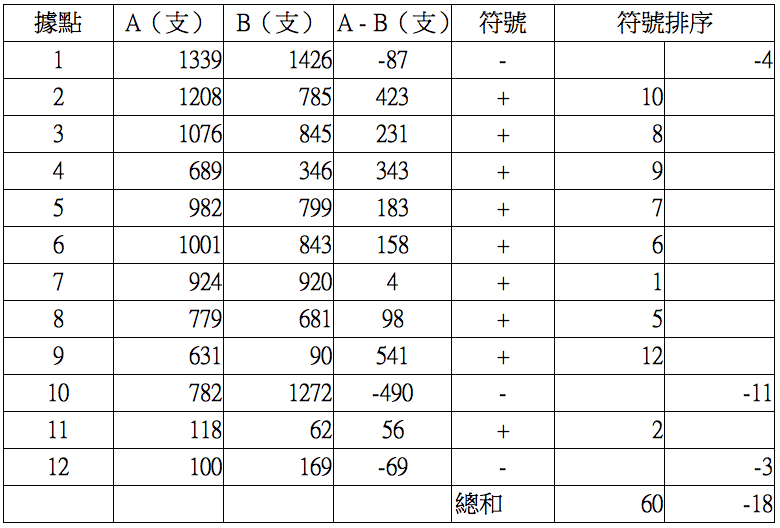
例如表一為某品牌兩款手機於各據點的銷售情況，欲檢驗是否 B 款式較 A 款式受消費者喜愛。威爾卡森符號檢定首先計算差值，若差值相同則捨棄該筆資料；接著以差值的數值（不考慮正負）標明排序，若排序相同（稱為排序同值，tie）則取平均排序值（例如兩筆差值同為 20，原本排序為 9、10，修正為 9.5、9.5；三筆差值皆為 15，原本排序為 6、7、8，則修正為 7、7、7）；最後加上符號並加總排序，整理表格如表一。

表一、兩款手機的銷售情況。（本文作者李韶凱製作）

假設 \(\alpha=0.05\) 的單尾檢定，虛無假設及對立假設分別為下：

\(H_0:M_A=M_B\)         \(H_a:M_A>M_B\)

其中 \(M_A\) 與 \(M_B\) 分別為 A 款式與 B 款式手機銷售量的中位數。假設 T 為正排序和及負排序和中的最小值，以下式子表示：

\(T=min\{|\text{正排序和}|,|\text{負排序和}|\}\)

當樣本數 \(n\ge 20\) 使用檢定統計量 Z 如下:

\(\displaystyle Z=\frac{|T-E(T)|}{\sqrt{Var(T)}}~~~~~~~~~(1)\)

若樣本數過小 \((n < 20)\) 則對檢定統計量進行連續性修正如下:

\(\displaystyle Z=\frac{|T-E(T)|-\frac{1}{2}}{\sqrt{Var(T)}}~~~~~~~~~(2)\)

而 T 值的期望值及變異數分別如下:

\(\displaystyle E(T) = (1+2+…+n) =\frac{n(n+1)}{4}\)

\(\displaystyle Var(T)=\frac{1}{2}(1^2+2^2+…+n^2)=\frac{n(n+1)(2n+1)}{24}\)

由例子中的數據可得：

\(T = min\{60,18\} = 18, E(T) = 39, Var(T) = 162.5\)

使用公式 (2) 計算檢定統計量得 Z = 1.61

查 Z 表得 \(\alpha=0.05\) 的 Z 值為 1.65 大於 1.61，因此無法拒絕 \(H_0\)，表示此抽樣資料可能表示消費者對兩款手機的喜惡程度相同或無特別偏好。以直覺而言，A 手機於多個據點銷量都較 B 手機好，但是由於樣本數過小，符號檢定和威爾卡森符號檢定的結果都無法得到顯著的結果，然而威爾卡森符號檢定的結果較接近棄卻域。

參考文獻

1. 沈明來 (2006)。生物統計學入門（第五版）。九州。頁180-190。
2. Hogg, R. V., Tanis, E., & Zimmerman, D. (2015). Probability and statistical inference (9^th edition). Pearson Higher Ed.