動態模擬軌跡方程式

動態模擬軌跡方程式
臺北市立西松高中蘇惠玉老師

在高中圓錐曲線的教材中，有一個教學目標為讓學生瞭解何謂軌跡方程式。藉由題目的設計，同時也讓學生理解圓錐曲線的來源，不是只有平面與圓錐的截痕，也不是只有按照定義方式才能得到。但是在學習過程中，學生們並不容易理解何謂動點（或動圓）？何謂軌跡？也很難從題目提供的條件「視覺化」的理解軌跡圖形為何？因此如果教師能夠藉由電腦軟體的模擬效果，將可讓學生輕易地經由「視覺」來理解幾何概念。以下為筆者整理在此單元教學時看過的幾個有關軌跡方程式的問題（問題來源皆為南一版學習講義第四冊），並試著以GeoGebra軟體來作動態模擬。

拋物線

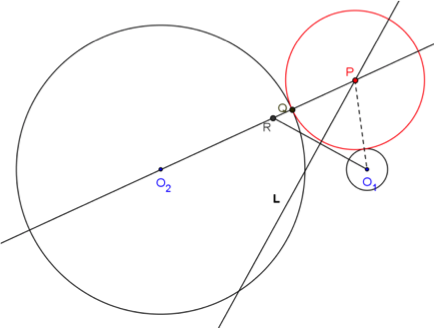
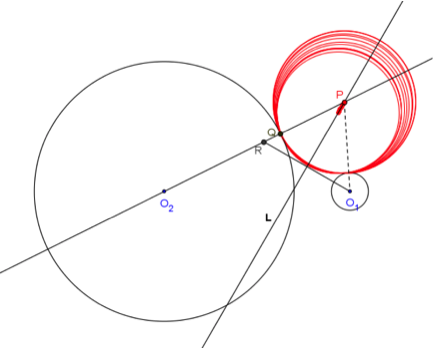
問題：設一動圓和直線 \(L:x+2=0\) 相切，且與圓 \(C:(x-4)^2+y^2=4\) 外切，求此動圓之圓心所成圖形的方程式。

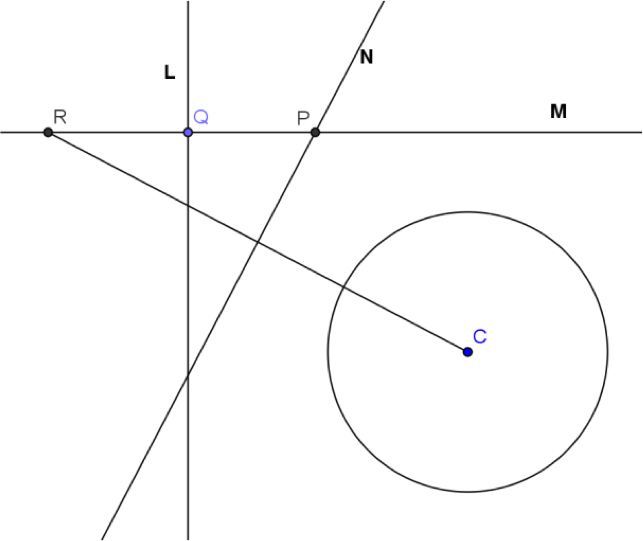
作圖步驟：

1. 作直線\(L:x+2=0\) 與圓 \(C:(x-4)^2+y^2=4\)，其圓心為 \(C\)
2. 在 \(L\) 上任取一點 \(Q\)，過 \(Q\) 作 \(L\) 的垂直線 \(M\)
3. 在直線 \(M\) 上，於 \(L\) 的另一側取 \(\overline{QR}\) 等於圓 \(C\) 的半徑 \(2\)
4. 作 \(\overline{RC}\) 的中垂線 \(N\)，與直線 \(M\) 交於一點 \(P\)，\(P\) 點即為所求圓之圓心

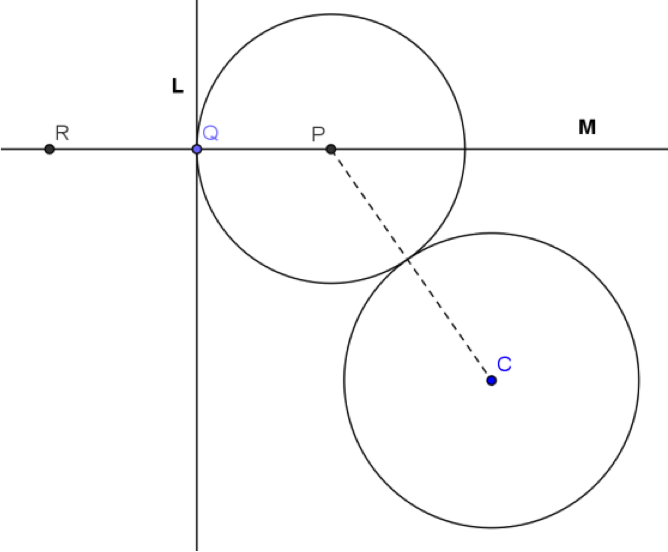
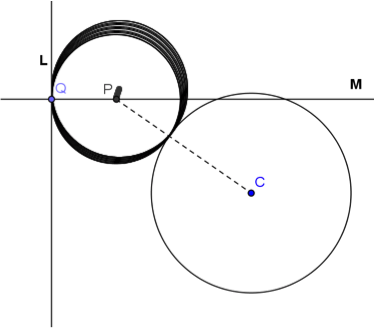
模擬過程：

1. 以 \(P\) 點為圓心，\(\overline{PR}\) 為半徑作圓，此圓即與直線 \(L\) 相切，又與圓 \(C\) 外切的圓。在此圓上按右鍵以顯示軌跡，讓 \(Q\) 點沿著 \(L\) 移動，即可看到這樣的圓跟著變成另一個，圓心也跟著變化，此即為「動圓」的意思。
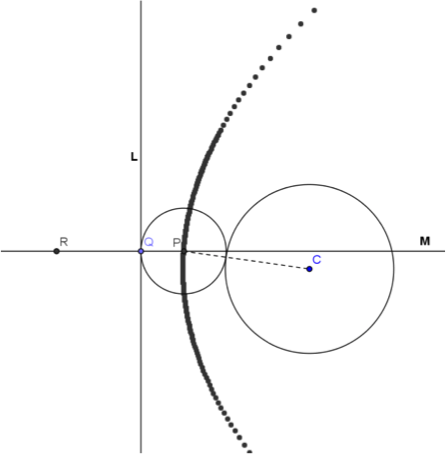
2. 取消圓的軌跡，換成顯示 \(P\) 點的軌跡，讓 \(Q\) 點沿著 \(L\) 移動，\(P\) 點的軌跡就可清楚看出為一拋物線。

橢圓

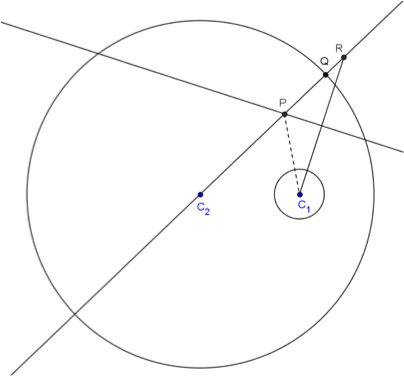
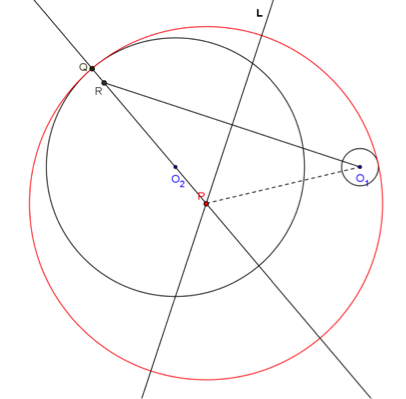
問題1：求與圓 \(C_1:(x-2)^2+y^2=1\) 外切，且與圓 \(C_2:(x+2)^2+y^2=49\) 內切之所有圓的圓心所成的圖形方程式。

作圖步驟：

1. 作圓 \(C_1:(x-2)^2+y^2=1\) 與圓 \(C_2:(x+2)^2+y^2=49\)，其圓心分別於 \(C_1\)、\(C_2\)
2. 在圓 \(C_2\) 上任取一點 \(Q\)，連直線 \(\overleftrightarrow{C_2Q}\)
3. 在圓 \(C_2\) 的外側之 \(\overleftrightarrow{C_2Q}\) 上，取 \(\overline{QR}\) 等於 \(C_1\) 的半徑 \(1\)
4. 作 \(\overline{C_1R}\) 的中垂線 \(L\)，與交 \(\overleftrightarrow{C_2Q}\) 於一點 \(P\)，即為所求圓心

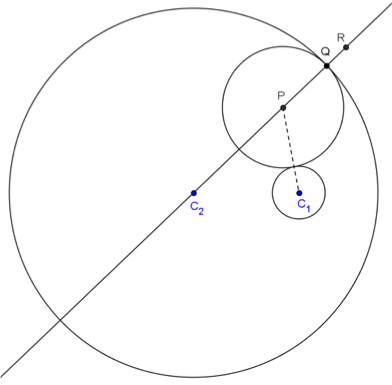
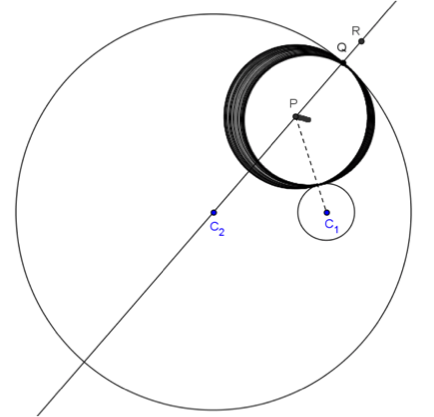
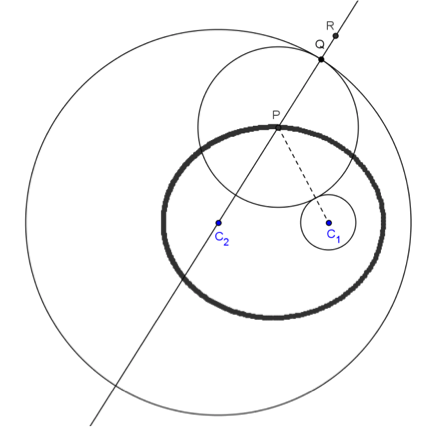
模擬過程：

以 \(P\) 點為圓心，\(\overline{PQ}\) 為半徑作圓，此圓即與圓 \(C_1\) 外切，又與圓 \(C_2\) 內切的圓。此時可在此圓上按右鍵以顯示軌跡，讓 \(Q\) 點沿著圓 \(C_2\) 移動，即可看到這樣的圓跟著變成另一個，圓心也跟著變化。取消圓的軌跡，換成顯示 \(P\) 點的軌跡，讓 \(Q\) 點沿著圓 \(C_2\) 移動，\(P\) 點的軌跡就可清楚看出為一橢圓。

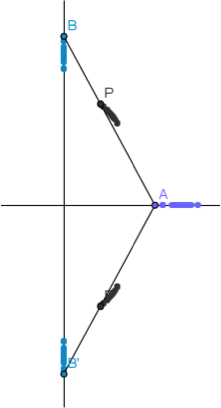
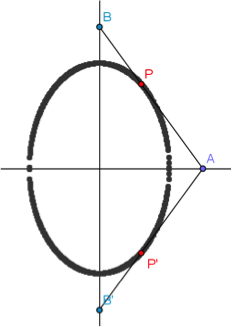
問題2：設 \(\overline{AB}=5\)，若 \(A\) 點在 \(x\) 軸上移動，\(B\) 點在 \(y\) 軸上移動，\(P\) 點在 \(\overline{AB}\) 上，且 \(\overline{AP}:\overline{BP}=3:2\)，求 \(P\) 點所成圖形的方程式。

作圖步驟：

1. 在 \(x\) 軸上取一點 \(A\)。
2. 以 \(A\) 為圓心，\(5\) 為半徑作圓，交 \(y\) 軸於 \(B\)、\(B’\) 兩點。
3. 連 \(\overline{AB}\)、\(\overline{AB’}\)。
4. 在 \(\overline{AB}\)（及 \(\overline{AB’}\)）上利用伸縮變換，以 \(A\) 為伸縮中心，將 \(B\) 點伸縮 \(\frac{3}{5}\) 倍得 \(P\) 點(及 \(P’\) 點)。
5. 讓 \(A\) 點沿著 \(x\) 軸移動，\(P\) 點的軌跡即為所求，圖形為一橢圓。

雙曲線

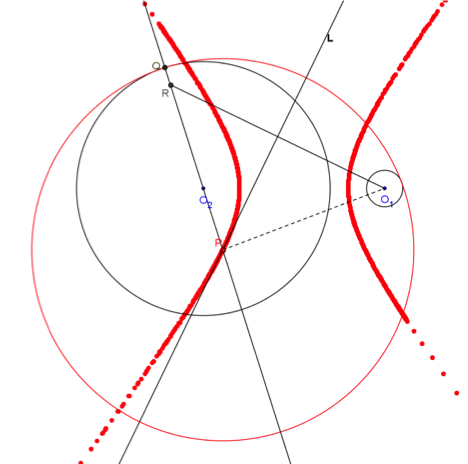
問題：設兩圓 \(C_1:(x-5)^2+y^2=1\) 與 \(C_2:(x+5)^2+y^2=49\)，求與圓 \(C_1\)、\(C_2\) 均內切或外切的動圓之圓心 \(P\) 所成圖形的方程式。

作圖步驟：

1. 作圓 \(C_1\) 與 \(C_2\)，其圓心分別為 \(O_1\)、\(O_2\)；
2. 在圓 \(C_2\) 上任取一點 \(Q\)，連直線 \(\overleftrightarrow{O_2Q}\)；
3. 在 \(\overleftrightarrow{O_2Q}\) 上，圓 \(C_2\) 的內部取一點 \(R\) 使得等於圓 \(C_1\) 的半徑 \(1\)；
4. 作 \(\overline{RO_1}\) 的中垂線 \(L\)，與 \(\overleftrightarrow{O_2Q}\) 交於一點 \(P\)，\(P\) 點即為所求之圓心

模擬過程：

以 \(P\) 點為圓心，\(\overline{PQ}\) 為半徑作圓，此圓即與同時與圓 \(C_1\)、\(C_2\) 外切，或是同時與圓 \(C_1\)、\(C_2\) 內切的圓。此時可在此圓上按右鍵以顯示軌跡，讓 \(Q\) 點沿著圓 \(C_2\) 移動，即可看到這樣的圓跟著變成另一個，圓心也跟著變化。取消圓的軌跡，換成顯示 \(P\) 點的軌跡，讓 \(Q\) 點沿著圓 \(C_2\) 移動，\(P\) 點的軌跡就可清楚看出為一橢圓。