重複組合（二）：公式的一個直觀解釋

重複組合（二）：公式的一個直觀解釋
Combination with repetition (II)：An intuitional explanation of the formula
臺北市立和平高中教師黃俊瑋

連結：重複組合（一）：相關課程之統整與反思 

在〈重複組合（一）：相關課程之統整與反思〉一文裡，簡單統整了重複組合相關概念與連結。

一般而言，重複組合問題可利用一一對應原理，轉化成 \(x_1+x_2+\cdots+x_n=k\) 類方程式求非負整數解個數問題，再進一步轉化得其解的數量為 \(C_k^{k+n-1}\)。而各類計數問題，只要轉化成上述方程式求非負整教解問題，便可依此組合公式求解。

以具體的例子來看，從 \(3\) 類物（每類物超過 \(5\) 個）可重複地選出 \(5\) 個的組合數，等於方程式 \(x+y+z=5\) 的非負整數解個數，可轉化成 \(5\) 個○與 \(2\) 個分隔記號|的排列數，再換成組合數，如此可知非負整數解之數為 \(C_3^{5+(3-1)}\)。

這裡筆者分享另一個想法：我們可將分隔記號「|」改以加號「＋」代替，這時 的一組解可對應到「○○○○○＋＋」的一種排法，例如：「○○＋○○＋○」\(\leftrightarrow(2,2,1)\)；「○＋＋○○○○」\(\leftrightarrow(1,0,4)\)，其中，將球區分成 \(3\) 區同樣需要兩個＋號，同時，加號可有助於直觀地與「\(3\) 個變數加起來為 \(5\)」，以及「\(3\) 類球○加起來共選 \(5\) 個」作連結。

然而，處理這類問題，除了進行多次轉換之外，上述組合數 \(C_3^{5+(3-1)}\) 是否有其它直觀的解釋或模型呢？筆者在此提出一例，供有興趣的讀者參考。

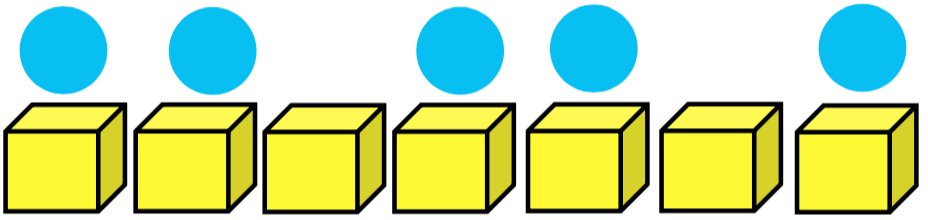
首先，我們取 \(5+(3-1)=7\) 個箱子排成一列（如圖一所示），接著，任選其中 \(5\) 個箱子各投入 \(1\) 個球（球相同），那麼，我們會發現，每一種選法皆可對應到一組非負整數解。如圖二所示，若選中第 \(1\)、\(2\)、\(4\)、\(5\)、\(7\) 個箱子，則對應到這組非負整數解。

圖一 七個排成一列的空箱

圖二 從七個排成一列的空箱選出五個各投入一個球

以下為了方便說明，我們以□□□□□□□代表 \(7\) 個空箱，投完球後，我們以□代表空箱，以●代表該箱已投入球，則有下列對應關係：

●●□●●□●\(\leftrightarrow(2,2,1)\)

●□□●●●●\(\leftrightarrow(1,0,4)\)

□●●□●●●\(\leftrightarrow(0,2,3)\)

□●●●●●□\(\leftrightarrow(0,5,0)\)

其中，由左數來第一個空箱左邊的●數，即為一組非負整數解 \((x_0,y_0,z_0)\) 的第一個未知數的值；第二個空箱左邊的●數，即為非負整數解的第二個未知數的值，以此類推，最後一個空箱的右邊的●數，則為解的最後一個未知數的值。請注意，投入球之後所剩的 \(2\) 個空箱，扮演了前述分隔記號「|」的角色。因此，空箱數需為 \(5+(3-1)=7\) 個。類似地，回到前述的相同物分配問題，其同樣與此模型間存在一一對應關係，例如：

●●□●●□●\(\leftrightarrow\)甲拿 \(2\) 個、乙拿 \(2\) 個、丙拿 \(1\) 個

□●●□●●●\(\leftrightarrow\)甲拿 \(0\) 個、乙拿 \(2\) 個、丙拿 \(3\) 個

以此類推。此方法亦可一般化，求 \(x_1+x_2+\cdots+x_n=k\) 的非負整數解時，需從 \(k+(n-1)\) 個空箱中選出 \(k\) 個來。

如此來看，無論是從 \(n\) 類物可重複地選出 \(k\) 個的重複組合問題、\(k\) 個相同物分配給 \(n\) 個人的問題，或者其它可化為求方程式 \(x_1+x_2+\cdots+x_n=k\) 非負整數解個數的各類問題，皆可想成從 \(k+(n-1)\) 個排成一列的空箱中，任意選出 \(k\) 個來投入球，則「選法」與前述各類問題情境所求的「方法數」存在一一對應的關係，因此，方法數皆為 \(C_k^{k+n-1}\)。以上供讀者與高中老師參考。