統計之旅：標準差公式 (I)

統計之旅：標準差公式 (I)
(Statistical Journey through the Formulas of Standard Deviation (I))
國立蘭陽女中教師 陳敏晧

一維的數值資料 \(x_1,x_2,…,x_n\)，

我們定義其標準差(standard deviation) 為 \({\sigma _x} = \sqrt {\displaystyle\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{x_i}-{\mu _x}}\right)}^2}}}\)，

其中 \(\sigma_x\) 讀為sigma x，而算術平均數 \(\mu_x\) 讀為mu x。

因此，從定義中可以理解標準差就是一維數值資料的離均差平方和的算術平均數再求其正平方根的值，其中的離均差為 \(\left| {{x_i} – {\mu _x}} \right|\)。

但是，通常在數學教學現場中，介紹完標準差的定義後，學生接著就會舉手發問，想要看出資料的分散或聚集程度為什麼一定要開根號呢？僅用四則運算不用開根號難道就真的看不出來？這是我個人每次在教標準差時所遇到的提問。

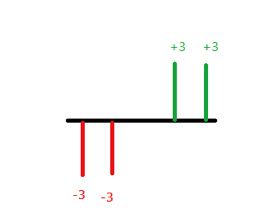
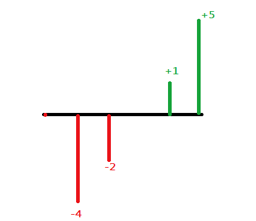
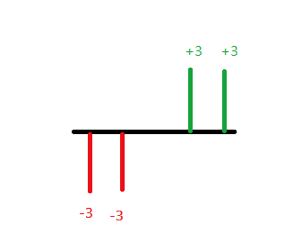
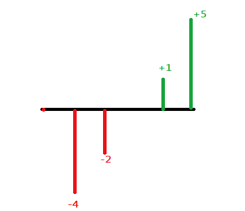
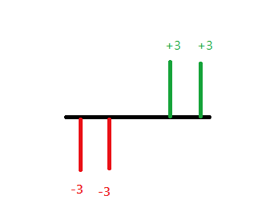
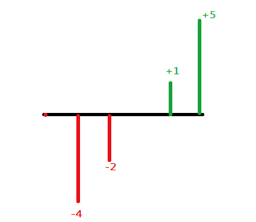
於是乎我想利用一些簡單的例子來推估統計學家為何如此定義標準差，以便說服這群學生，如果有兩筆資料分別為 \(3,3, – 3, – 3\) 及 \(5,1,-2,-4\)，可以清楚看出兩筆資料的算術平均數都是零，即 \({\mu _1} = \frac{{3 + 3 + ( – 3) + ( – 3)}}{4} = 0,{\mu _2} = \frac{{5 + 1 + ( – 2) + ( – 4)}}{4} = 0\)。

第一種情形：若把標準差定義為 \({\sigma _x} =\displaystyle\frac{1}{n}\sum\limits_{i = 1}^n {({x_i} – {\mu _x})}\)，
則第一筆資料的標準差 \({\sigma _1} =\displaystyle\frac{1}{4}\left[ {\left( {3 – 0} \right) + (3 – 0) + ( – 3 – 0) + ( – 3 – 0)} \right] = 0\)。

圖一 作者陳敏晧繪

第二筆資料的標準差 \({\sigma _2} =\displaystyle \frac{1}{4}\left[ {\left( {5 – 0} \right) + (1 – 0) + ( – 2 – 0) + ( – 4 – 0)} \right] = 0\)。

圖二 作者陳敏晧繪

所以，\({\sigma _1} = {\sigma _2} = 0\)，
因此，若標準差的定義採用 \({\sigma _x} =\displaystyle\frac{1}{n}\sum\limits_{i = 1}^n {({x_i} – {\mu _x})}\) 是無法看出資料的差異程度。

第二種情形：若把標準差定義為 \({\sigma _x} =\displaystyle\frac{1}{n}\sum\limits_{i = 1}^n {\left| {{x_i} – {\mu _x}} \right|}\)，
則第一筆資料的標準差 \({\sigma _1} =\displaystyle\frac{1}{4}\left[ {\left| {3 – 0} \right| + \left| {3 – 0} \right| + \left| { – 3 – 0} \right| + \left| { – 3 – 0} \right|} \right] = 3\)。

圖三 作者陳敏晧繪

第二筆資料的標準差 \({\sigma _2} =\displaystyle\frac{1}{4}\left[ {\left| {5 – 0} \right| + \left| {1 – 0} \right| + \left| { – 2 – 0} \right| + \left| { – 4 – 0} \right|} \right] = 3\)。

圖四 作者陳敏晧繪

雖然 \({\sigma _1} = {\sigma _2} = 3\)，但依舊無法看出兩筆不同資料的差異程度，
因此標準差的定義不得採用 \({\sigma _x} =\displaystyle\frac{1}{n}\sum\limits_{i = 1}^n {\left| {{x_i} – {\mu _x}} \right|}\)。

第三種情形：接著統計學家嘗試把標準差定義為 \({\sigma _x} = \sqrt {\displaystyle\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{x_i} – {\mu _x}} \right)}^2}}}\)，
則第一筆資料的標準差 \({\sigma _1} = \sqrt {\displaystyle\frac{1}{4}\left[ {{{\left( {3 – 0} \right)}^2} + {{\left( {3 – 0} \right)}^2} + {{\left( { – 3 – 0} \right)}^2} + {{\left( { – 3 – 0} \right)}^2}} \right]}= 3\)，
答案跟第一情形與第二情形相同。

圖五 作者陳敏晧繪

第二筆資料的標準差則為 \({\sigma _2} = \sqrt {\displaystyle\frac{1}{4}\left[ {{{\left( {5 – 0} \right)}^2} + {{\left( {1 – 0} \right)}^2} + {{\left( { – 2 – 0} \right)}^2} + {{\left( { – 4 – 0} \right)}^2}} \right]}=\sqrt {11.5}\approx 3.4\)

圖六 作者陳敏晧繪

這個結果很令人滿意，
因此不難想像為什麼標準差的定義最後會採用 \({\sigma _x} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{x_i} – {\mu _x}} \right)}^2}} }\)，
言談至此，似乎已經引發教室內同學的興趣，
那麼定 \({\sigma _x} = \sqrt[3]{{\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{x_i} – {\mu _x}} \right)}^3}} }}\) 如何？

因為開奇數次方，運算過程中的正負值會抵消，數值間的差異就會被忽略，所以，不適用；

若定 \({\sigma _x} = \sqrt[4]{{\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{x_i} – {\mu _x}} \right)}^4}} }}\) 則是因為開方次數過大，運算起來恐怕不甚方便，最後，統計學家定調標準差的定義為 \({\sigma _x} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{x_i} – {\mu _x}} \right)}^2}} } \)；最後提醒一件事情，標準差的單位與原測量單位一致。

若從幾何學的角度出發，

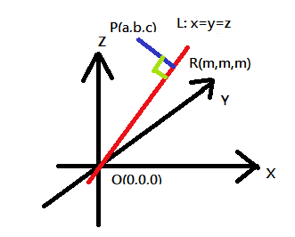
若取空間中一點 \(P(a,b,c)\)，取空間中一直線 \(L:\frac{{x – 0}}{1} = \frac{{y – 0}}{1} = \frac{{z – 0}}{1}\)，即 \(L:x=y=z\)，

過點 \(P(a,b,c)\) 做 \(\overline {PR}\bot L\) 交於 \(R\) 點，

令 \(R(m,m,m)\) 也就是 \((m-a,m-b,m-c)\cdot (1,1,1)=0\)，

得 \((m-a)+(m-b)+(m-c)=0\)，

所以，\(m = \displaystyle\frac{{a + b + c}}{3} = {\mu _x}\)，

換言之 \(\overline {PR}= \sqrt {{{(a – {\mu _x})}^2} + {{(b – {\mu _x})}^2} + {{(c – {\mu _x})}^2}}= \sqrt 3 {\sigma _x}\)，

如圖七所示，因此，在 \(n\) 維空間中，點到直線的距離可以視為 \(\sqrt{n}\sigma_x\)。

這個事實，賦予了標準差的一種幾何意涵。

圖七 作者陳敏晧繪

連結：統計之旅：標準差公式 (II)

參考文獻

1. Moses, Lincoln E. (1986) Think and Explain with Statistics, Addison-Wesley, pp. 12–13.