巴斯卡與數學歸納法（Pascal and Mathematical Induction）

巴斯卡與數學歸納法（Pascal and Mathematical Induction）
國立台南第一高級中學數學科林倉億老師/國立臺灣師範大學數學系許志農教授責任編輯

摘要:本文介紹巴斯卡在其著作《論算術三角形》中的推論12，以及巴斯卡在證明推論12所用的方法與今日數學歸納法的關係。

巴斯卡（Blaise Pascal，1623-1662）因「巴斯卡三角形」而廣為中學學生所認識，然而，大部分中學生以及中學老師並不知道，巴斯卡在《論算術三角形》（A treatise on the Arithmetical Triangle）一書中，除了介紹「算術三角形」（即俗稱的「巴斯卡三角形」）外，還利用了「疑似的」數學歸納法來證明其中的性質，因此，巴斯卡曾被認為是最早使用數學歸納法的人。為什麼說「疑似的」呢？請繼續看下去。

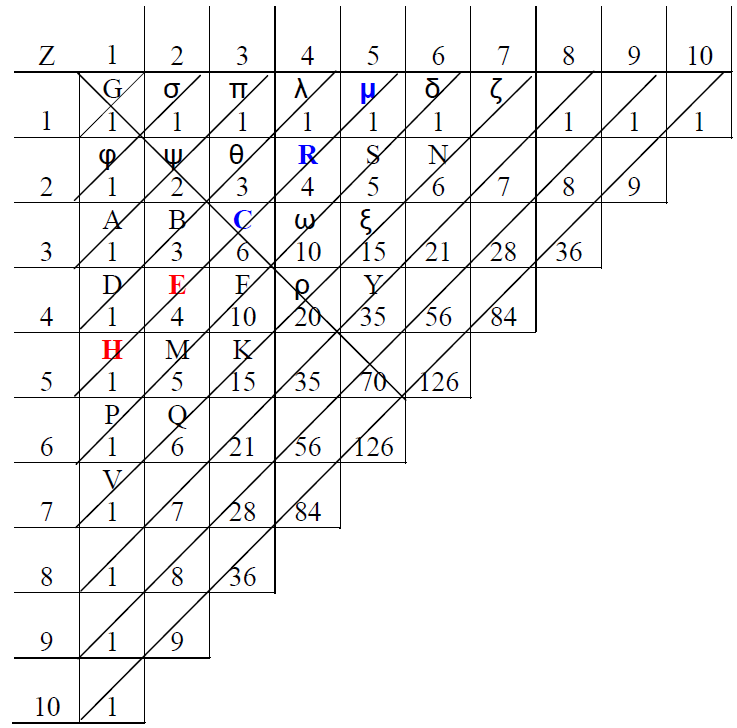
巴斯卡從「算術三角形」中得到許多的結論，他稱之為推論，並寫入《論算術三角形》一書中。《論算術三角形》雖然約在1654 年就完成了，但一直到巴斯卡死後才出版。讀者可利用網路連結至英國劍橋大學圖書館的「Digital Images Collections of Cambridge University Library」（網址：http://www.lib.cam.ac.uk/digital_image_collections/），一睹此書的原貌。巴斯卡在推論12 中寫道（請同時參閱上圖）：

在同一底上的兩個相鄰的格子，位置在上的格子（上格）與位置在下的格子（下格）的數字比，等於從此上格到此底的頂格的格子數與從下格到底端的格數的比，而此上、下格都包含在其中。

考慮同底上任一兩相鄰格 E、C，我斷言：

E 比 C (下格比上格 ) ＝ 2 ( 從E 到底端有兩格，即E、H) ：3 (從C 到頂端有三格，即C、R、μ）

用現今的符號表示，推論12 的意思就是 $$C^n_{k}:C^n_{k+1}=(k+1):(n-k)$$ 。巴斯卡明瞭不可能將無窮  多種情形都一一證明，因此，他藉助了兩個引理：

引理1：本身即是證據。這個命題在第二底時顯然成立；因為很明顯地 $$\varphi$$ 比 $$\sigma$$ 等於 $$1$$ 比 $$1$$。
引理2：假設此命題在某一底為真時，則可得到在其下一底也一定為真。

然後他說：「從以上可知在所有的底都為真，因為在引理1 中，第二底為真；所以由引理2 知第三底亦為真，從而在第四底亦為真，如此以至無窮。所以僅需證明引理2 即可。」

至此，相信熟悉數學歸納法的讀者應該很快地就能將引理1、2 與數學歸納法中的兩個步驟連結在一起。的確，若故事就止於此，那巴斯卡毫無疑問的就是使用數學歸納法的第一人。然而，當時數學歸納法之基礎─自然數的皮亞諾公設（註一）尚未問世，因此，巴斯卡並不認為可以直接使用引理2，反而認為有必要證明它。他對引理2 的證明如下（請同時參閱上圖）：

設此命題在某一底為真，如在第四底Dλ 上為真，即D 比B 等於1 比3，B 比θ 等於2比2，且θ 比λ 等於3 比1，等等。則我說在下一底Hμ 上也有同樣的比例，例如E 比C等於2 比3。由假設知，D 比B 等於1 比3，於是D＋B 比B 等於 (1＋3) 比3， 而D＋B＝E，所以E 比B 等於4 比3 同樣的方法，由假設知B 比θ 等於2 比2，於是B＋θ比B 等於(2＋2)比2，而B＋θ＝C，所以C 比B 等於4 比2 而B 比E 等於4 比3，由合比定理得C 比E 等於3 比2。證明完畢。

巴斯卡自己也很清楚這樣子的證明難杜攸攸之口，因此他在「證明完畢」後加強說明：「在所有其他的底上，都可以用同樣的方法證明，因為這樣的證明方式僅建立在這樣的事實上：命題在前一底為真，且每一格都等於它的前一格（左邊的格子）與其上面一格的和，而這一點對每一種情況都成立。」

若從今日的眼光來看，稱呼巴斯卡是最早使用數學歸納法的人，並不妥當。可是，數學並非一蹴可幾的，而是後人不斷地在前人的成果上繼續累積、貢獻。因此，我們該換個角度看待巴斯卡的證明。從巴斯卡的證明中，我們可以發現他已經充分地認知到藉由引理1 與引理2，將可以面對有無窮多種情況的挑戰。就這一點來說，巴斯卡對數學歸納法的發展，就有不可磨滅的貢獻。

註一：皮亞諾（Giuseppe Peano，1858~1932）在1889 年發表的《算術原理》（Arithmetics Principia）中，利用邏輯符號給出自然數的公設（axiom），其中之一的「若一自然數集 $$S$$ 包含 $$1$$，且若自然數 $$x \in S$$ 則 $$x+1\in S$$，則 $$S$$ 包含所有自然數」，可視為數學歸納法的邏輯基礎。

參考資料：

1. 蘇惠玉 (2005)，「數學歸納法的證明形式之完成」，HPM通訊，第八卷第四期，第1-7頁（網址：http://math.ntnu.edu.tw/~horng/letter/804.pdf）
2. 李文林主編 (2000)，《數學珍寶》，台北：九章出版社。