和算家求橢圓周長的方法（二）（Wasan’s method of finding the formula of the circumference of an ellipse Ⅱ）

和算家求橢圓周長的方法（二）
（Wasan’s method of finding the formula of the circumference of an ellipse Ⅱ）
臺北市立和平高中教師黃俊瑋

連結：和算家求橢圓周長的方法（一）

如前文〈和算家求橢圓周長的方法（一）〉所述，和田寧是最早造出正確橢圓周長展開式的數學家，然而，他的主要著作皆在西元1836年的一場大火中付之一炬，因此，我們只得以他授予的弟子們的傳書，一窺他求解橢圓周長的方法。

和田寧的弟子小出兼政，依據和田寧所授之傳書編成《圓理算經》，該書〈上卷〉的第五部份裡，提出了求橢圓周長問題：「譬今有如圖橢圓，只言長徑若干，短徑若干，問得周長術如何？」作者造橢圓周長公式的過程中，主要是利用分割求和的積分方式，輔以各類「圓理表」。以下，筆者進一步說明並分析他求橢圓周長的過程。

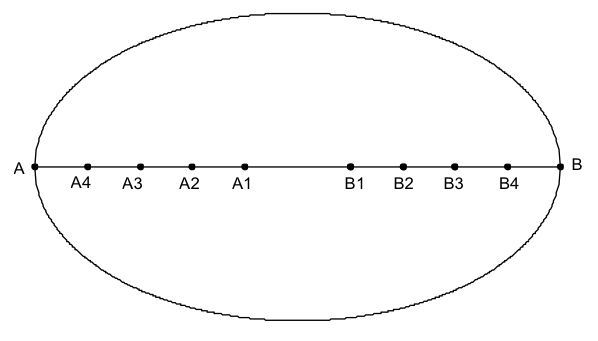
假設橢圓之長軸長為 \(2a\)、短軸長為 \(2b\)，首先，小出兼政先利用「截弦順法對橢圓之長軸作分割，配對得到 \(n\) 段，讀者請參考圖一，以分割成配對 \(5\) 等分的情況為例作說明。此分割法是以左右配對 \(5\) 等分割的方式，對橢圓之長軸作分割，使其滿足：

 \(\overline{{A_1}{B_1}}=\overline {{A_1}{A_2}}+\overline {{B_1}{B_2}}=\overline{{A_2}{A_3}}+\overline{{B_2}{B_3}}= \overline{{A_3}{A_4}}+\overline{{B_3}{B_4}}=\overline{{A_4}A}+\overline{{B_4}B}=\frac{{2a}}{5}\)

這和現代教科書中所用的等分割方式有所不同。

圖一\(~~\)截弦順法截橢圓之長軸

圖二\(~~\)《圓理算經》求橢圓周術之參照圖

接著，他再「依圖檢矩線表」，根據這個表，利用已知的「長軸長 \(2a\)」、「短軸長 \(2b\)」再搭配勾股定理，最終可表示第 \(k\) 段左右配對弧長的近似值，亦即圖二之中左右配對弧長  的近似值為 \(\overline{{P_k}{P_{k + 1}}}+\overline{{Q_k}{Q_{k + 1}}}={L_k}\)，他稱此近似值為某背較，並整理得此值為：

\(\displaystyle\frac{{\frac{{2a}}{n}\sqrt {1 – {{(\frac{k}{n})}^2}(1 – \frac{{{{(2b)}^2}}}{{{{(2a)}^2}}})} }}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}\)

而後，小出兼政為了簡化代數式，令式子中的 \(1 – \frac{{{{(2b)}^2}}}{{{{(2a)}^2}}} = e\)，則可將某背較 \(L_k\) 表示成：

\(\displaystyle\frac{{\frac{{2a}}{n}}}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}\sqrt {1 – {{(\frac{k}{n})}^2}e}\)

接著，他又查「應率八象表之陽商乘表」，此表所列即為 \({\left( {1 – x} \right)^{\frac{{2k – 1}}{2}}}\) 二項展開式之中的各項係數。這裡令 \(x=(\frac{k}{n})^2e\)，便可依該表，將 \(\sqrt {1 – {{(\frac{k}{n})}^2}e}\) 作展開，得某背較 \(L_k\) 如下：

\(\displaystyle{L_k} = \frac{{\frac{a}{n}}}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}(1 – \frac{1}{2}e{(\frac{k}{n})^2} – \frac{1}{8}{e^2}{(\frac{k}{n})^4} – \frac{3}{{48}}{e^3}{(\frac{k}{n})^6} – \frac{{15}}{{384}}{e^4}{(\frac{k}{n})^8} – …)\)

然而，這只是上半橢圓某段弧長(第 \(k\) 段)的近似值，求所有的某背較之和 \(\sum\limits_{k = 1}^n {{L_k}}\)，便是上半橢圓周的近似值。當 \(n\) 趨近於無窮大，意即分割區間的寬度趨近於 \(0\) 時，兩倍某背較和的極限值便是橢圓周長，即 \(L = 2\mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n {{L_k}}\)。

因此，小出兼政需再將各段近似值「某背較 \(L_k\)」相加再「取級限」求得真正的弧長。

而他所查的「見飛表之龍商除陽表」，便濃縮了上述求「某背較」和與取極限的兩個動作，

如此可求得上半橢圓周長 \(\frac{L}{2} = \mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n {{L_k}}\)，而整個橢圓周長便是 \(2\mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n {{L_k}}\)。

若以現代符號表示，整個檢表過程相當如下代數關係：

\(\begin{array}{ll}L &= 2\mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n {{L_k}}\\&=\displaystyle 2\mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n [ \frac{{\frac{{2a}}{n}}}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}(1 – \frac{1}{2}e{(\frac{k}{n})^2} – \frac{1}{8}{e^2}{(\frac{k}{n})^4} – \frac{3}{{48}}{e^3}{(\frac{k}{n})^6} – \frac{{15}}{{384}}{e^4}{(\frac{k}{n})^8}-\cdots)]\\&=\displaystyle4a(\mathop{\lim}\limits_{n\rightarrow\infty }\sum\limits_{k=1}^n{\frac{{\frac{1}{n}}}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}}-\frac{1}{2}e\mathop{\lim }\limits_{n\rightarrow\infty}\sum\limits_{k=1}^n{\frac{{{{(\frac{k}{n})}^2}\cdot\frac{1}{n}}}{{\sqrt{1-{{(\frac{k}{n})}^2}}}}}-\frac{1}{8}{e^2}\sum\limits_{k=1}^n{\frac{{{{(\frac{k}{n})}^4} \cdot\frac{1}{n}}}{{\sqrt{1-{{(\frac{k}{n})}^2}}}}}-\cdots\frac{3}{{48}}{e^3}\mathop{\lim}\limits_{n\rightarrow\infty} \sum\limits_{k=1}^n{\frac{{{{(\frac{k}{n})}^6}\cdot\frac{1}{n}}}{{\sqrt{1-{{(\frac{k}{n})}^2}}}}}-\frac{{15}}{{384}}{e^4}\sum\limits_{k=1}^n{\frac{{{{(\frac{k}{n})}^8}\cdot\frac{1}{n}}}{{\sqrt {1-{{(\frac{k}{n})}^2}}}}}-\cdots~~~~~~~~~(*)\end{array}\)

針對上述各項 \(\displaystyle\mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n {\frac{{{{(\frac{k}{n})}^{2i}} \cdot \frac{1}{n}}}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}}\)，查「見飛表之龍商除陽表」之後，

可分別求得：\(\displaystyle\mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n {\frac{{\frac{1}{n}}}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}}=\frac{\pi }{2}\)、\(\displaystyle\mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n {\frac{{{{(\frac{k}{n})}^2} \cdot \frac{1}{n}}}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}}=\frac{1}{2} \cdot \frac{\pi }{2}\)、\(\displaystyle\mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n {\frac{{{{(\frac{k}{n})}^4} \cdot \frac{1}{n}}}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}}=\frac{3}{8} \cdot \frac{\pi }{2}\)、\(\displaystyle\mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n {\frac{{{{(\frac{k}{n})}^6} \cdot \frac{1}{n}}}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}}=\frac{{15}}{{48}} \cdot \frac{\pi }{2}\)、\(\displaystyle\mathop {\lim }\limits_{n\rightarrow\infty } \sum\limits_{k = 1}^n {\frac{{{{(\frac{k}{n})}^8} \cdot \frac{1}{n}}}{{\sqrt {1 – {{(\frac{k}{n})}^2}} }}}=\frac{{105}}{{384}} \cdot \frac{\pi }{2}\)。

最後，代入（*）式，可得如下之橢圓周長展開式：

\(\displaystyle L = 2a\pi (1 – \frac{1}{2} \cdot \frac{1}{2}e – \frac{3}{8} \cdot \frac{1}{8}{e^2} – \frac{{15}}{{48}} \cdot \frac{3}{{48}}{e^3} – \frac{{105}}{{384}} \cdot \frac{{15}}{{384}}{e^4} – …)\)

其中的 \(e = 1 – \frac{{{{(2b)}^2}}}{{{{(2a)}^2}}}\)。最後，小出兼政也進一步找到前後項係數之間的關係，並將原級數表示成如下形式：

\(L = \pi (2a – \sum\limits_{k = 1}^\infty{{D_k}} )\)

其中 \(D_0=2a\)、\(D_1=D_0T\)、\({D_{k + 1}} = \frac{{(2k – 1) \cdot (2k + 1)}}{{{{(k + 1)}^2}}}{D_k}T\)、\(T = \frac{1}{4}e = \frac{1}{4}[1 – \frac{{{{(2b)}^2}}}{{{{(2a)}^2}}}]\)、\(k \ge 1\)。

此時，橢圓周術可進一步表示成：

\(L = \pi (2a – \frac{1}{{{1^2}}}T \cdot {D_0} – \frac{{1 \cdot 3}}{{{2^2}}}T \cdot {D_1} – \frac{{3 \cdot 5 \cdot }}{{{3^2}}}T \cdot {D_2} – \frac{{5 \cdot 7}}{{{4^2}}}T \cdot {D_3} – …)\)

以上，便是和算家造橢圓周長公式的方法。在沒有函數與解析幾何等工具之下，他們主要是利用分割求積分法，輔以和算家所造的各類圓理表，包含二項展開式表與無窮級數和表（亦可看成積分數值表）等，再搭配相關圖形之間的幾何關係，最終求得了正確的橢圓周長公式。除了上述橢圓周長問題外，和算家也利用類似的積分法，解決了許多即便是微積分也難以處理的求弧長、求面積與體積問題，即便是兩相交立體所截成立體之體積、表面積、截面積、截周長等涉及複雜積分或雙重積分的問題，和算家亦是依此法求解。而和田寧所發展出的這套「積分法」，正是十九世紀和算家最重要的解題利器，也標誌了和算發展的最後一個高峰。

參考文獻：

• 小出兼政，《圓理算經》，1842年。