從複數到三角函數公式(II) (From complex number to trigonometric function formulas)

從複數到三角函數公式(II) (From complex number to trigonometric function formulas)
國立蘭陽女中陳敏晧教師

連結：從複數到三角函數公式(I) 

證明：

(1) \(\displaystyle\sin \theta+ \sin 2\theta+\cdots+ \sin n\theta= \frac{{\sin \frac{{(n + 1)\theta }}{2} \cdot \sin \frac{{n\theta }}{2}}}{{\sin \frac{\theta }{2}}}\)

(2) \(\displaystyle\cos \theta+\cos 2\theta+\cdots+ \cos n\theta= \frac{{\sin \frac{{n\theta }}{2}\cos \frac{{(n + 1)\theta }}{2}}}{{\sin \frac{\theta }{2}}}\)

第二種證明方法：利用複數的概念。

我們可以使用歐拉公式 \({e^{i\theta }}= \cos \theta+ i\sin \theta\)，

若將 \(\theta\) 以 \(-\theta\) 代入可得 \({e^{ – i\theta }}= \cos \theta- i\sin \theta\)，

可得 \(\left\{ \begin{array}{l}\displaystyle \cos \theta= \frac{{{e^{i\theta }}+ {e^{ – i\theta }}}}{2}\\\displaystyle\sin \theta = \frac{{{e^{i\theta }}-{e^{ – i\theta }}}}{{2i}} \end{array} \right.\)，變換變數得 \(\left\{ \begin{array}{l}\displaystyle\cos \frac{\theta }{2} = \frac{{{e^{\frac{{i\theta }}{2}}} + {e^{\frac{{ – i\theta }}{2}}}}}{2}\\\displaystyle\sin \frac{\theta }{2} = \frac{{{e^{\frac{{i\theta }}{2}}} – {e^{\frac{{ – i\theta }}{2}}}}}{{2i}} \end{array} \right.\)

，將上式令為

\(\begin{array}{ll}y+ix&= (\cos \theta+\cos 2\theta+\cdots+ \cos n\theta )+ i(\sin \theta+\sin 2\theta+\cdots+ \sin n\theta )\\&= (\cos \theta+ i\sin \theta )+ (\cos 2\theta+ i\sin 2\theta )+\cdots+ (\cos n\theta+ i\sin n\theta )\\&= (\cos \theta+i\sin \theta )+{(\cos \theta+i\sin \theta )^2}+\cdots+ {(\cos \theta+ i\sin \theta )^n}\\&= {e^{i\theta }}+{e^{i2\theta }} +\cdots+ {e^{in\theta }}\end{array}\)
\(\begin{array}{ll}~~~~~~~~&=\frac{{{e^{i\theta }} \cdot (1 – {e^{in\theta }})}}{{1 – {e^{i\theta }}}}\end{array}\)，分母 \(1 – {e^{i\theta }} = {e^{\frac{{i\theta }}{2}}} \cdot ({e^{\frac{{ – i\theta }}{2}}} – {e^{\frac{{i\theta }}{2}}}) = {e^{\frac{{i\theta }}{2}}}( – 2i\sin \frac{\theta }{2})\)
\(\begin{array}{ll}~~~~~~~~&=\displaystyle\frac{{{e^{i\theta }} \cdot (1 – {e^{in\theta }})}}{{{e^{\frac{{i\theta }}{2}}}( – 2i\sin \frac{\theta }{2})}}\\&=\displaystyle \frac{{{e^{\frac{{i\theta }}{2}}} – {e^{\frac{{i(2n + 1)\theta }}{2}}}}}{{ – 2i\sin \frac{\theta }{2}}}\\&=\displaystyle\frac{{\cos \frac{\theta }{2} + i\sin \frac{\theta }{2} – \cos \frac{{(2n + 1)\theta }}{2} – i\sin \frac{{\left( {2n + 1} \right)\theta }}{2}}}{{ – 2i\sin \frac{\theta }{2}}}\\&=\displaystyle\frac{{(\sin \frac{{(2n + 1)\theta }}{2} – \sin \frac{\theta }{2}) + i(\cos \frac{\theta }{2} – \cos \frac{{(2n + 1)\theta }}{2})}}{{2\sin \frac{\theta }{2}}}\end{array}\)

因此，\(\displaystyle{y}= \cos \theta+ \cos 2\theta+\cdots+ \cos n\theta= \frac{{\sin \frac{{(2n + 1)\theta }}{2}-\sin \frac{\theta }{2}}}{{2\sin \frac{\theta }{2}}}=\frac{{\sin \frac{{n\theta }}{2}\cos \frac{{(n + 1)\theta }}{2}}}{{\sin \frac{\theta }{2}}}\\\displaystyle{x}= \sin \theta+\sin 2\theta+\cdots+\sin n\theta= \frac{{\cos \frac{\theta }{2}- \cos \frac{{(2n + 1)\theta }}{2}}}{{2\sin \frac{\theta }{2}}}=\frac{{\sin \frac{{n\theta }}{2} \cdot \sin \frac{{(n + 1)\theta }}{2}}}{{\sin \frac{\theta }{2}}}\)

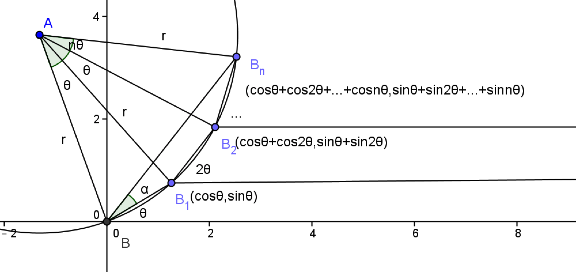
第三種證明方法：圖形証法。

如上圖所示，我們令 \(\overline{BB_1}=1\)，且 \(\overline{BB_1}\) 與 \(x\) 軸之夾角為 \(\theta\)，

再過點 \(B_1\) 做另一條線段 \(\overline{B_1B_2}=1\)，並使其與第一條線段 \(\overline{BB_1}\) 的夾角為 \(\theta\)，

所以，\(\overline{B_1B_2}\) 與 \(x\) 軸之夾角為 \(2\theta\)，以此類推做 \(n\) 次，得到點 \(B_n\)，

利用對同弧時圓周角等於其所對圓心角的性質，

則 \(B,B_1,B_2,\cdots,B_n\) 都在以 \(A\) 為圓心的圓周上，

令 \(B\left( {0,0} \right),{B_1}\left( {\cos \theta ,\sin \theta } \right),{B_2}(\cos \theta+\cos 2\theta ,\sin \theta+\sin 2\theta )\)，以此類推，

令 \({B_n}(\cos \theta+ \cos 2\theta+\cdots+ \cos n\theta ,\sin \theta+\sin 2\theta+\cdots+\sin n\theta )\)，

在 \(\Delta ABB_1\) 中，因為 \(\overline{AB}=\overline{AB_1}\)，所以 \(\angle AB{B_1} = \angle A{B_1}B = {90^\circ} – \frac{\theta }{2}\)，

根據正弦定理，即 \(\displaystyle\frac{{\overline {AB} }}{{\sin ({{90}^\circ} – \frac{\theta }{2})}} = \frac{{\overline {B{B_1}} }}{{\sin \theta }}\)，

利用正弦二倍角公式，得到 \(\displaystyle\overline {AB}= \frac{{1 \cdot \cos \frac{\theta }{2}}}{{\sin \theta }} = \frac{{\cos \frac{\theta }{2}}}{{2\sin \frac{\theta }{2}\cos \frac{\theta }{2}}} = \frac{1}{{2\sin \frac{\theta }{2}}}\)，

接著考慮 \(\Delta AB{B_n}\)，因為頂角 \(\angle BA{B_n}= n\theta\)，則底角 \(\angle AB{B_n} = \angle A{B_n}B = {90^\circ} – \frac{{n\theta }}{2}\)，

再根據正弦定理及正弦二倍角公式 \(\displaystyle\frac{{\overline {AB} }}{{\sin ({{90}^\circ} – \frac{{n\theta }}{2})}} = \frac{{\overline {B{B_n}} }}{{\sin n\theta }}\)，

化簡得 \(\displaystyle\overline {BB_n}= \overline {AB}\cdot \frac{{\sin n\theta }}{{\cos \frac{{n\theta }}{2}}}= \frac{1}{{2\sin \frac{\theta }{2}}} \cdot \frac{{2\sin \frac{{n\theta }}{2} \cdot \cos \frac{{n\theta }}{2}}}{{\cos \frac{{n\theta }}{2}}}= \frac{{\sin \frac{{n\theta }}{2}}}{{\sin \frac{\theta }{2}}}\)，

利用圓周角性質 \(\angle {B_1}B{B_n} = \frac{1}{2}\angle {B_1}A{B_n} = \frac{{(n – 1)\theta }}{2}\)，即圖上 \(\alpha= \frac{{(n – 1)\theta }}{2}\)，

算得 \(\alpha+ \theta= \frac{{\left( {n – 1} \right)\theta }}{2}+ \theta= \frac{{(n + 1)\theta }}{2}\)，

最後根據正弦與餘弦定義得

\(\displaystyle\cos \theta+ \cos 2\theta+\cdots+\cos n\theta= \overline {B{B_n}}\cdot \cos \frac{{(n + 1)\theta }}{2}= \frac{{\sin \frac{{n\theta }}{2} \cdot \cos \frac{{(n + 1)\theta }}{2}}}{{\sin \frac{\theta }{2}}}\)

\(\displaystyle\sin \theta+ \sin 2\theta+\cdots+ \sin n\theta= \overline {B{B_n}}\cdot \sin \frac{{(n + 1)\theta }}{2}= \frac{{\sin \frac{{n\theta }}{2} \cdot \sin \frac{{(n + 1)\theta }}{2}}}{{\sin \frac{\theta }{2}}}\)

歐拉公式 \({e^{i\pi }} + 1 = 0\) 常常被譽為數學界中最美的公式。

最後，筆者引《博士熱愛的算式》第163頁做為結語：

歐拉從這些看似毫無關係的數字中，發現彼此之間自然的關聯：「\(e\) 的 \(\pi\) 和 \(i\) 之積的次方再加上 \(1\)，就變成了 \(0\)。」我重新看著博士的紙條。永無止境循環下去的數字，和讓人難以捉摸的虛數畫出簡潔的軌跡，在某一點落地。雖然沒有圓的出現，但來自宇宙的 \(\pi\) 飄然來到 \(e\) 的身旁，和害羞的 \(i\) 握著手。他們的身體緊緊靠在一起，屏住呼吸；但有人加了 \(1\) 以後，世界就毫無預警發生了巨大的變化，一切都歸於 \(0\)。

參考文獻：

1. 毛爾著，胡守仁譯，《毛起來說三角》，台北：天下遠見出版社，2000年。
2. 小川洋子著，王蘊潔譯，《博士熱愛的算式》，台北：麥田出版社，2004年。
3. 葉文傑，〈複數法在中學數學中的應用〉，《數學傳播》，37卷2期，頁80-92。