條件機率(3)：一個問題的澄清（Conditional Probability (3)：Clarifying a problem）

條件機率(3)：一個問題的澄清（Conditional Probability (3)：Clarifying a problem）
臺北市立第一女子高級中學蘇俊鴻老師

連結：條件機率(2)：乘法定律

再次重述在〈條件機率(2)：乘法定律〉中所提出問題：

某人拜訪有兩個孩子的一對夫婦，當場已有一個男孩在座。假設生男生女的機會相等，求此夫婦兩小孩皆為男孩的機率？

或許幾經思考，這個問題總讓你聯想對應到〈條件機率(1)：定義〉中提及的某個典型的例題：

投擲公正硬幣兩次，已知擲出一次正面的情形下，求投擲兩次皆為正面的機率。

那麼，何以機率為 \(\frac{1}{3}\)，這個看來似乎正確答案值得商榷？這正是本文的目的，透過這個問題的討論，希望能夠建立起將機率應用在實際生活問題時，需要更加小心的印象。以下容我們加以說明原由。

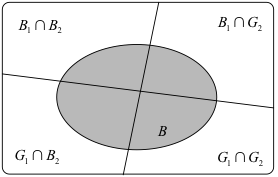
為了便於說明，不妨令 \(B_1,B_2\) 分別表示老大，老二是男孩的事件；

\(G_1,G_2\) 分別表示老大、老二是女孩的事件；\(B\) 則表示在座為男孩的事件。

進一步，我們可知 \(\{ {B_1} \cap {B_2},{B_1} \cap {G_2},{G_1} \cap {B_2},{G_1} \cap {G_2}\}\) 恰為我們所討論樣本空間的一組分割，且 \(P({B_1} \cap {B_2}) = P({G_1} \cap {B_2}) = P({B_1} \cap {G_2}) = P({G_1} \cap {G_2}) = \frac{1}{4}\)。

同時，\({B_1} \cap {B_2} \subset B\)，\({G_1} \cap {G_2} \cap B = \emptyset \)，而問題所求恰為 \(P({B_1} \cap {B_2}|B)\)。

依題意，\(P({B_1} \cap {B_2}|B) = \frac{{P({B_1} \cap {B_2} \cap B)}}{{P(B)}} = \frac{{P({B_1} \cap {B_2})}}{{P(B)}}\)

由上圖可知，

\(\begin{array}{ll}P(B) &= P(B \cap {B_1} \cap {B_2}) + P(B \cap {G_1} \cap {B_2}) + P(B \cap {B_1} \cap {G_2}) + P(B \cap {G_1} \cap {G_2})\\&= \frac{1}{4} + P(B \cap {G_1} \cap {B_2}) + P(B \cap {B_1} \cap {G_2})\end{array}\)

由於問題並沒有提供說明在座男孩的資訊，我們不妨考慮下列幾個情形：

情形一

若因訓練禮儀之故，這對夫婦要求有客人到訪時，家中小孩務必有一人需要在場。令老大在場的機率為 \(p\)，則老二在場的機率為 \(1-p\)。

那麼，\(P(B \cap {B_1} \cap {G_2}) = \frac{p}{4}\)，\(P(B \cap {G_1} \cap {B_2}) = \frac{{1 – p}}{4}\)

則 \(P(B) = \frac{1}{4} + \frac{{1 – p}}{4} + \frac{p}{4} = \frac{1}{2}\)

因此，\(\displaystyle P({B_1} \cap {B_2}|B) = \frac{{\frac{1}{4}}}{{\frac{1}{2}}} = \frac{1}{2}\)

看見了嗎？在情形一之下，問題的機率為 \(\frac{1}{2}\)，且與 \(p\) 值無關。接著，考慮另一種可能的情況。

情形二

當兩小孩性別不同時，這對夫婦要求有客人到訪時，家中男孩務必需要在座。

那麼，\(P(B \cap {B_1} \cap {G_2}) = \frac{1}{4}\)，\(P(B \cap {G_1} \cap {B_2}) = \frac{1}{4}\)。

則 \(P(B) = \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{3}{4}\)

因此，\(\displaystyle P({B_1} \cap {B_2}|B) = \frac{{\frac{1}{4}}}{{\frac{3}{4}}} = \frac{1}{3}\)

這說明問題的答案 \(\frac{1}{3}\) 也是可能之一，以及此答案成立的情形。

進一步，在情形二中若令家中男孩在座的機率為 \(p\)，則此條件機率 \(P({B_1} \cap {B_2}|B)\) 是 \(p\) 的函數 \((0\le p \le 1)\)。

從上述的說明可知，上述問題所涉及的樣本空間不只是 \({B_1} \cap {B_2},{B_1} \cap {G_2},{G_1} \cap {B_2},{G_1} \cap {G_2}\) 等4個元素，還需要加上小孩排序的因素。我們若要完整討論，得要列出有 \(8\) 個元素的樣本空間才夠，這從題意中很難直接看到，恐怕得要是個相當熟稔條件機率，且能縝密考慮的解題者才能圓滿解出！無怪乎黃文璋教授在〈機率應用不易〉一文特別提到：「機率很難，尤其條件機率。」這話不只在勉勵初學機率的學生，恐怕更想勸誡老師們在布題時要多加謹慎才是。此外，這篇〈機率應用不易〉的文章，深入地討論機率之困難掌握的問題，其中也涵蓋本文所舉的問題，有興趣的讀者，不妨尋來讀之，收獲必定良多。

參考文獻：

• 黃文璋，〈機率應用不易〉，《數學傳播》，34(1)(台北：2010)，頁14-28。