西方行列式的發展:結語(The Development of Determinants in West: Concluding Remarks)
西方行列式的發展:結語
(The Development of Determinants in West: Concluding Remarks)
國立臺南第一高級中學林倉億老師
行列式在西方萌芽後,在數學家們辛勤地澆灌、耕耘下,歷經了100多年,終於成熟。為行列式發展做出的數學家很多,〈西方行列式的發展〉系列文章只挑選了其中幾位作簡要的介紹,其他未寫到的數學家如拉格朗日 (Joseph Lagrange, 1736-1813)、拉普拉斯 (Pierre-Simon marquis de Laplace, 1749-1827)、比內 (Jacques Philippe Marie Binet, 1786-1856)、雅可比 (Carl Gustav Jacob Jacobi, 1804-1851)、凱萊 (Arthur Cayley, 1821-1895)、西爾維斯特 (James Joseph Sylvester, 1814-1897)……等等,都對20世紀之前的行列式發展,做出了不可抹滅的貢獻。
從歷史的發展,我們很清楚地看到,西方的行列式發展是從一次方程組求解開始的,數學家們發現用係數來表示方程組的解時,是有規律可循的。為了表示這規律,數學家們提出了不同的方式。
以三元一次方程組 \(\left\{ \begin{array}{l} {a_{1}}x + {b_{1}}y + {c_{1}}z = {d_{1}}\\ {a_{2}}x + {b_{2}}y + {c_{2}}z = {d_{2}}\\ {a_{3}}x + {b_{3}}y + {c_{3}}z = {d_{3}} \end{array} \right.\)為例,克拉瑪利用 \(a_ib_jc_k\) 下標的排列與逆序數來表示其規律(參閱本網站〈克拉瑪公式(2):克拉瑪的公式〉一文);貝祖將 \(abc\) 與 \(-bac\) 的 \(c\) 不斷地往前移動一個位置,並每移動一個位置就要改變一次性質符號(參閱本網站〈西方行列式的發展:貝祖的研究〉一文);范德蒙與柯西則以其獨特的方式來定義行列式(參閱本網站〈西方行列式的發展:范德蒙的研究〉與〈西方行列式的發展:柯西的研究〉)。
就在追尋規律表達式的過程中,行列式的概念、符號,慢慢地成為今日的模樣。
然而,在今日的高中課堂中,行列式以抽象符號及展開式呈現在學生面前,略去了歷史發展脈絡,也難以激起學生的學習動機。比方說,對於二階行列式 \(\left| {\begin{array}{*{20}{c}} a&b\\ c&d \end{array}} \right|\) 的性質推演,學生常常感到不耐,總覺得直接乘開,\(ad-bc\),一切清清楚楚,何必大費周章。
又例如大多數學生初接觸到三階行列式及其展開式
\(\begin{array}{ll}\left| {\begin{array}{*{20}{c}} {{a_{1}}}&{{a_{2}}}&{{a_{3}}}\\ {{b_{1}}}&{{b_{2}}}&{{b_{3}}}\\ {{c_{1}}}&{{c_{2}}}&{{c_{3}}} \end{array}} \right| &=\cdots\cdots \\&= {a_{1}}{b_{2}}{c_{3}} + {a_{2}}{b_{3}}{c_{1}} + {a_{3}}{b_{1}}{c_{2}} – {a_{3}}{b_{2}}{c_{1}} – {a_{2}}{b_{1}}{c_{3}} – {a_{1}}{b_{3}}{c_{2}}\end{array}\)
時,其表情是狐疑的,甚至是嫌惡的,彷彿在告訴老師說:「為什麼要規定這麼奇怪的運算規則?」歷史的發展是從上述等式的最右邊發展到最左邊的,先有了行列式展開後的式子,過了100多年後,才有今日行列式的符號。
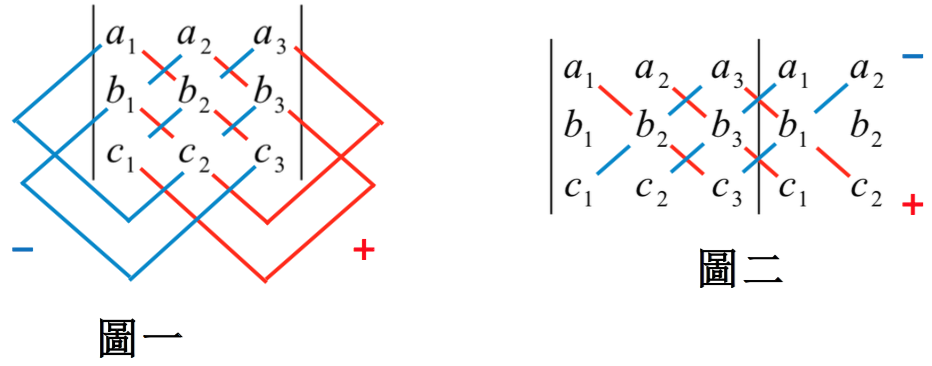
然而,今日教材的呈現,常常是反其道而行的,從等號的最左邊走到等號的最右邊。這方向一反,不但抹去了人類100多年來的心血成果,更嚴重的是扼殺了學生對行列式的好奇心。行列式對學生來說,只是一種規定的計算法則,背下來就對了!然而,諷刺的是,最值得記的,總是不在學生腦海中。筆者最喜歡玩的把戲之一,就是給一個四階行列式(不在高中課程之內)要學生展開,大多數的學生會毫不遲疑地將記得的三階行列式展開法,即圖一與圖二的方法,套用在四階行列式上,然後得到只有8項的展開式,而且完全不會感覺到有任何不妥的地方!(應該要有24項)
圖一與圖二代表的是三階行列式的一種記憶法或速算法,在時間有限的紙筆測驗中,常常是最有效率的解題手段,這也是它們最大的優點。但若撇開計算速度,它們相較於克拉瑪或貝祖的方法,不僅無趣,更不能推廣到高階的行列式。倘若能在課堂中引入克拉瑪或貝祖的方法,甚至是范德蒙或柯西的方式,不僅能開拓學生的眼界,更能降低行列式符號的神祕感,幫助學生掌握行列式的概念與符號。
行列式從解聯立方程組而來,逐漸變成一個獨立的數學概念與符號,然後再應用到不同的領域之中,例如幾何、向量、矩陣,最後再被納入線性代數的架構之中。筆者這系列文章只概略地描繪了前段的發展歷史,至於後來應用的精彩篇章,就留待以後有機會再作介紹了。


 前一篇文章
前一篇文章 下一篇文章
下一篇文章 惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題  海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria)  泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2)) 
