標準狀況下理想氣體與真實氣體間的焓值差－以C2H6為例 (二)

標準狀況下理想氣體與真實氣體間的焓值差－以C2H6為例 (二)
The enthalpy difference between the ideal gas and real gas under standard condition – a case study in C2H6 (II)
國立臺灣師範大學化學系兼任教師 邱智宏

連結：標準狀況下理想氣體與真實氣體間的焓值差－以C₂H₆為例 (一)

二、伯特洛方程式和臨界點

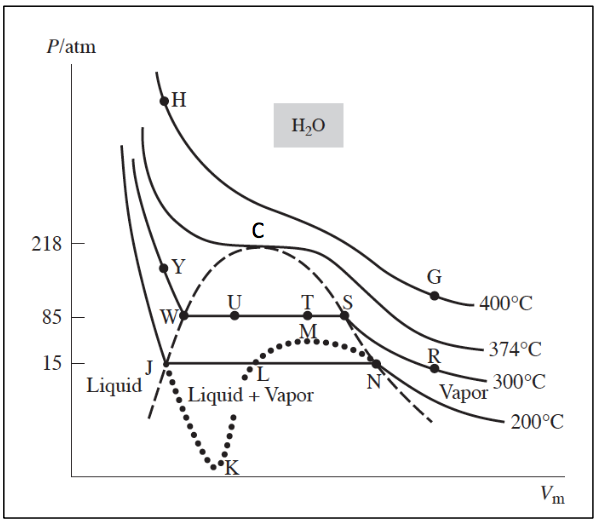
欲求出不同氣態物質在伯特洛方程式中的 $$a$$、$$b$$ 數值，則需對此方程式稍作瞭解。現以水蒸氣為例，以壓力對莫耳體積作圖，在 $$200^\circ C$$ 時，會出現一段水平線(NLJ)，即體積減小壓力不變，此時開始有氣體凝結為液體，當溫度愈高時，水平的部分逐漸減短，到 $$374^\circ C$$ 時，水平線成為一點$$(C)$$，此點稱為臨界點( critical point )，此時液、氣間的界面消失，此點的溫度及壓力分別為臨界溫度$$(T_c)$$及臨界壓力$$(p_c)$$。

圖一 $$~~~$$水的等溫線，在虛線範圍內氣、液二相共存，範圍外僅存一相，虛線的最高點為臨界點。逗點線為利用凡得瓦爾方程式計算的等溫線。 （取自參考資料1, p.215）

在臨界點時，$$\displaystyle (\frac{\partial p}{\partial V_m})_T=0,(\frac{\partial^2 p}{\partial V^2_m})_T=0$$ ，因此利用此特性，可求出該物質之伯特洛方程式在臨界點時，$$a$$、$$b$$ 值和 $$T_c$$、$$p_c$$ 間的關係。因此將伯特洛方程式即 $$(2)$$ 式對莫耳體積微分

$$\displaystyle (\frac{\partial p}{\partial V_m})_T=\frac{-RT}{(V_m-b)^2}+\frac{2a}{TV^3_m},~(\frac{\partial^2 p}{\partial V^2_m})_T=\frac{2RT}{(V_m-b)^3}-\frac{6a}{TV^4_m}$$

上列二式在臨界點 $$(T=T_c,p=p_c)$$ 時均等於 $$0$$，所以可簡化如下：

$$\displaystyle \frac{RT_c}{(V_{m,c}-b)^2}=\frac{2a}{T_cV^3_{m,c}},~\frac{2RT_c}{(V_{m,c}-b)^3}=\frac{6a}{T_cV^4_{m,c}}$$

將上列二式相除可得 $$V_m=3b$$，再將其代回 $$(2)$$ 式及上式，經過適當簡化，可得 $$a$$、$$b$$ 與 $$T_c$$、$$p_c$$ 間的關係如下：

$$\displaystyle a=\frac{27R^2T_c^3}{64p_c},~b=\frac{RT_c}{8p_c}$$

將上式代入 $$(11)$$ 式可得下式：

$$\displaystyle H^\circ_{m,id}-H^\circ_{m,re}\approx (\frac{3a}{RT^2}-b)p^0=(\frac{81RT_c^3}{64T^2p_c}-\frac{RT_c}{8p_c})p^0~~~~~~~~~(12)$$

三、$$\mathrm{C_2H_6}$$ 於 $$298.15~K$$ 的 $$H^\circ_{m,id}-H^\circ_{m,re}$$

經過冗長的推導，終於得到立即可用的 $$(12)$$ 式，只要將欲求物質的臨界溫度、臨界壓力及標準壓力，溫度代入，便可求出理想氣體與真實氣體間的焓值差，還好各物質的臨界壓力及溫度均為可查的實驗數據。經查 $$\mathrm{C_2H_6}$$ 的 $$T_c=305.4~K$$、$$p_c=48.2~atm$$，欲求 $$1~bar$$、$$298.15~K$$ 時的差異情況，可代入 $$(11)$$ 式，其計算結果所下：

$$\begin{array}{ll} H^\circ_{m,id}-H^\circ_{m,re} &\approx\displaystyle(\frac{81RT_c^3}{64T^2p_c}-\frac{RT_c}{8p_c})p^0\\&=\displaystyle(\frac{81\times 8.314\times 305.4^3}{64\times 298.15^2\times 48.2\times 101325}-\frac{8.314\times 305.4}{8\times 48.2\times 101325})\times 100000\\&=\displaystyle 62.54~J\cdot mol^{-1}\end{array}$$

由上式算出 $$H^\circ_{m,id}-H^\circ_{m,re}$$ 的值約為 $$62.54~J\cdot mol^{-1}$$，和實際的實驗值 $$62.70~J\cdot mol^{-1}$$ 比較，其相對誤差不到千分之 $$3$$。實際查表 $$\mathrm{C_2H_6}$$ 的莫耳生成焓為 $$-84.68~kJ\cdot mol^{-1}$$，雖然理想氣體與真實氣體間的焓值差佔整體莫耳生成焓的比例很小，但理論上仍是不可以省略的部分。

四、結論

本文以 $$\mathrm{C_2H_6}$$ 為實例計算在標準狀態為 $$1~bar$$、$$298.15~K$$ 時，其理想氣體與真實氣體間的相對焓相差多少。由計算結果顯示，兩者之間實際相差不大，僅佔整體莫耳生成焓的千分之一，但在理論上，仍舊是不可以忽略的部分。本文所利用模擬真實氣體的方程式，是使用伯特洛方程式，由於在低溫的情況，它的準確度比凡得瓦爾方程式來得準確，至於高溫的情況則恰好相反。整個公式的推導過程，除了伯特洛方程式以外，為了微分的便利性，尚使用了維里方程式及泰勒展開式等，足見數學的推導在物化課程中所扮演的重要角色。

另外，要求得純物質的莫耳生成焓$$(\Delta_f H^\circ_m)$$，事實上要經過下列6個步驟，現以 $$\mathrm{C_2H_6}$$ 為例說明如下：

1. 生成 $$\mathrm{C_2H_6}$$ 的成份元素，在 $$1~bar$$、$$298.15~K$$ 時，石墨為固體，$$\mathrm{H_2}$$ 為氣體，兩者的相對焓雖均為零，但此時的 $$\mathrm{H_2}$$ 視為理想氣體，實際上在卡計中反應的 $$\mathrm{H_2}$$ 卻是真實氣體，因此需將其轉為真實氣體時的相對焓：算出 $$\Delta H_1$$。
2. 計算所有成份元素在 $$1~bar$$、$$15~K$$ 時混合時焓的變化量：$$\Delta H_2$$，在此例中僅有一種氣體，没有混合的問題，其值為 $$0$$。
3. 將混合物從 $$1~bar$$、$$298.15~K$$，提升至其在卡計內能完全反應的溫度及壓力，
   此時焓的變化量：$$\Delta H_3$$，可經由右式算出：$$\Delta H_3=\int_{298}^T C_p\mathrm{d}T+\int_{p^0}^p(V-TV\alpha)\mathrm{d}p$$。
   左式等號右邊的第一項為溫度由參考狀態的溫度 $$25^\circ C$$ 變成 $$T$$ 時所造成的焓變化，第二項則為壓力由標準壓力$$(p^0)$$改變成 $$p$$ 時焓的變化量，由於反應物已非理想氣體，真實氣體焓的變化不再只是溫度的函數，壓力也會影響。其中 $$\alpha=\frac{1}{V_m}(\frac{\partial V_m}{\partial T})_p$$，此式必需有真實氣體中 $$V_m$$ 和 $$T$$ 的關係，才有辦法微分，簡化的方法可以使用凡得瓦爾方程式(van der Waals equation)模擬真實氣體。
4. 利用卡計測量反應完全轉變為產物時焓的變化量：$$\Delta H_4$$。
5. 將反應後產物的溫度及壓力，再調回標準狀態，利用步驟3相同的方式，可以求出 $$\Delta H_5$$。
6. 反應後的產物：$$\mathrm{C_2H_6}$$，為真實氣體，因此必須再調回規定的理想氣體狀態，其間焓的變化量即為 $$\Delta H_6=H^\circ_{m,id}-H^\circ_{m,re}$$。

上列6個步驟中，其中 $$\Delta H_4$$ 為最主要的貢獻者，但是精密的計算時，其他步驟亦不可省略，所以 $$\Delta_f H^\circ_m=\Delta H_1+\Delta H_2+\Delta H_3+\Delta H_4+\Delta H_5+\Delta H_6$$。本文所介紹的部分僅為上列步驟中的第6個步驟，至於其他部分，學子若有興趣，可自行參考物化的教科書籍或閱讀高瞻計畫資源平台的相關文章。

參考文獻

1. N. Levine(1988), Physical Chemistry (3rd ed.). p211~225, McGRAW-HILL Book Company.
2. 標準狀況下理想氣體與真實氣體間的熵值差－以SO₂為例，高瞻計畫資源平台，http://highscope.ch.ntu.edu.tw/wordpress/?s=邱智宏