標準狀況下理想氣體與真實氣體間的熵值差－以SO2為例(一)

標準狀況下理想氣體與真實氣體間的熵值差－以SO2為例(一)
The entropy difference between the ideal gas and real gas under standard condition – a case study in SO2 (I)
國立臺灣師範大學化學系兼任教師 邱智宏

純物質的焓(enthalpy)、自由能(Gibbs free energy)及熵(entropy)是化學熱力學經常要使用到的數據，因此一般化學教科書均會將一些常見物質的相關數據，表列在附錄中，以供參考及使用。但是這些數據是如何求得的？卻鮮少被討論，尤其表列純物質的熵，若在標準狀態下為氣體，則其設定的情況為該氣體為理想氣體。

事實上理想氣體的標準莫耳相對熵$$(S^\circ_{m,id})$$和真實氣體的標準莫耳相對熵$$(S^\circ_{m,re})$$是不一樣的，它們之間的差距是多少？本文擬以 $$\mathrm{SO_2}$$ 為例，利用熱力學的公式，按部就班的推導它們之間的差異，除了讓學子利用所學，真正應用在解決問題上，也期盼學子能感受到在計算過程中數學所扮演的重要角色。

一、標準狀態和公式推導

一般列表的熱力學數據，均有其訂定的標準狀態(standard state)，通常為 $$1~bar$$ 下的某特定溫度，此溫度若為 $$298.15~K$$，則以 $$S^\circ_{m,298.15}$$ 表示在 $$298.15~K$$ 的標準莫耳相對熵(standard state molar conventional entropy)，其中上標 $$\circ$$ 表示標準壓力為 $$1~bar$$，下標的 $$m$$ 表示單位莫耳。另外，氣態純物質的標準狀態是假設其為理想氣體，而非真實氣體。

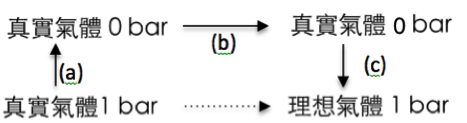
既然表列的標準狀態為 $$1~bar$$、$$298.15~K$$，此時 $$\mathrm{SO_2}$$ 被視為理想氣體，其標準莫耳相對熵為 $$248.22~J\cdot mol^{-1}\cdot K^{-1}$$，若其為真實氣體則兩者之間會相差多少呢？由於熵是狀態函數，因此定溫下，要計算由 $$1~bar$$ 真實氣體變成同狀況下理想氣體的熵之變化量$$(S^\circ_{m,id}-S^\circ_{m,re})$$，亦可經由下列(a)、(b)、(c)三步驟完成，即 $$\Delta S_a+\Delta S_b+\Delta S_c$$。

其中(a)步驟，可由馬克士威關係式(Maxwell relations)推導：

$$\displaystyle (\frac{\partial S}{\partial p})_T=-(\frac{\partial V_m}{\partial T})_p\Rightarrow \Delta S_a=-\int_{p^0}^0(\frac{\partial V_m}{\partial T})_p\mathrm{d}p=\int_0^{p^0}(\frac{\partial V_m}{\partial T})_p \mathrm{d}p$$

至於步驟(b)在壓力為 $$0~bar$$ 時，分子間的引力為 $$0$$，此時真實氣體和理想氣體相同，因此 $$\Delta S_b=0$$。

步驟(c)理想氣體從 $$0~bar$$ 到 $$1~bar$$，其熵的變化量亦可由上列的馬克士威關係式推導，另外由於是理想氣體，所以 $$pV_m=RT$$，可將下式簡化：

$$\displaystyle \Delta S_c=-\int_0^{p^0}(\frac{\partial V_m}{\partial T})_p \mathrm{d}p=-\int_0^{p^0}\frac{R}{p}\mathrm{d}p$$

經過上列推導，在 $$1~bar$$ 下真實氣體變成理想氣體的熵的變化量為：

$$\displaystyle S_{m,id}^\circ-S_{m,re}^\circ=\Delta S_a+\Delta S_b+\Delta S_c=\int^{p^0}_0[(\frac{\partial V_m}{\partial T})_p-\frac{R}{p}]\mathrm{d}p~~~~~~~~~(1)$$

上式中的$$(\frac{\partial V_m}{\partial T})_p$$必須得知真實氣體之溫度和體積間的關係式才能做積分，一般較常用的為凡得瓦爾方程式(van der Waals equation)或伯特洛方程式(Berthelot’s equation)，將其與維里方程式(virial equation)比較，經過適當簡化，便能求出$$(\frac{\partial V_m}{\partial T})_p$$的關係，由於在低壓下使用伯特洛方程式所求得的相對熵，比凡得瓦爾方程式準確，因此我們使用前者繼續往下推導。

首先伯特洛方程式描述真實氣體的方程式如下：

$$\displaystyle p=\frac{RT}{V_m-b}-\frac{a}{TV_m^2}~~~~~~~~~(2)$$

它的表示法和凡得瓦爾方程式幾乎一樣，僅等式右邊第二項的分母多了一個 $$T$$，因此雖為同一物質，其 $$a$$、$$b$$ 的數值也和凡得瓦爾方程式的不一樣。事實上 $$(2)$$ 式要直接求出$$(\frac{\partial V_m}{\partial T})_p$$的微分關係式相當複雜，因此要經過適當的轉換，先將 $$(2)$$ 式以壓縮因素(compress factor)表示

$$\displaystyle Z=\frac{pV_m}{RT}=(\frac{RT}{V_m-b}-\frac{a}{TV_m^2})\frac{V_m}{RT}=(\frac{1}{1-\frac{b}{V_m}}-\frac{a}{RT^2V_m})~~~~~~~~~(3)$$

由泰勒展開式可知

$$\begin{array}{l}\displaystyle \frac{1}{1-x}=1+x+x^2+x^3+\cdots & for~|x|<1\end{array}$$

$$(2)$$ 式中的b約略等於該氣體液態時的體積，因此其值顯然遠小於氣體的體積，因此 $$\frac{b}{V_m}<1$$ ，所以 $$(3)$$ 式中的 $$\frac{1}{1-\frac{b}{V_m}}$$，若以泰勒展開式展開，則可表示如下：

$$\displaystyle Z=(\frac{1}{1-\frac{b}{V_m}}-\frac{a}{RT^2V_m})=1+(\frac{b}{V_m}-\frac{a}{RT^2V_m})+(\frac{b}{V_m})^2+(\frac{b}{V_m})^3+\cdots$$

上式若和下式以體積表示的維里方程式比較可看出，等號右邊的第二項應該相等

$$\displaystyle Z=\frac{pV_m}{RT}=1+\frac{B}{V_m}+\frac{C}{(V_m)^2}+\frac{D}{(V_m)^3}+\cdots~~~~~~~~~(4)$$

即 $$\displaystyle (\frac{b}{V_m}-\frac{a}{RT^2V_m})=(\frac{B}{V_m})$$，所以可得下式：

$$\displaystyle B=b-\frac{a}{RT^2}~~~~~~~~~(5)$$

由上式可知，$$(4)$$ 式中的維里係數(virial coefficients) $$B$$、$$C$$、$$D$$ 等均為 $$T$$ 的函數。$$(4)$$ 式中的 $$B$$ 值雖可透過伯特洛方程式中的 $$a$$、$$b$$ 求出，但是 $$(4)$$ 式要將莫耳體積對溫度做微分，依舊非常困難，但是若使用以壓力表示的維里方程式則相對簡單，其表示法如下：

$$\displaystyle Z=\frac{pV_m}{RT}=1+B^\dagger(p)+C^\dagger(p)^2+D^\dagger(p)^3+\cdots~~~~~~~~~(6)$$

若對 $$(6)$$ 式移項，並將莫耳體積對溫度微分如下，當然其中的係數 $$B^\dagger,C^\dagger,D^\dagger\cdots$$ 亦均為 $$T$$ 的函數。

$$\displaystyle pV_m=RT[1+B^\dagger (p)+C^\dagger (p)^2+D^\dagger (p)^3+\cdots]~~~~~~~~~(7)$$

$$\displaystyle V_m=\frac{RT}{p}[1+B^\dagger (p)+C^\dagger (p)^2+D^\dagger (p)^3+\cdots]$$

$$\begin{multline*}\displaystyle (\frac{\partial V_m}{\partial T})_p=\frac{R}{p}[1+B^\dagger (p)+C^\dagger (p)^2+D^\dagger (p)^3+\cdots]\\+\frac{RT}{p}[\frac{\partial B^\dagger}{\partial T}p+\frac{\partial C^\dagger}{\partial T}p^2+\frac{\partial D^\dagger}{\partial T}p^3+\cdots]\end{multline*}$$

$$\displaystyle (\frac{\partial V_m}{\partial T})_p=\frac{R}{p}+R(B^\dagger+\frac{T\partial B^\dagger}{\partial T})+Rp(C^\dagger+\frac{T\partial C^\dagger}{\partial T})+\cdots$$

將上式代入 $$(1)$$ 式

$$\begin{array}{ll}\displaystyle S^\circ_{m,id}-S^\circ_{m,re}&=\displaystyle\int_0^{p^0}\Big[(\frac{\partial V_m}{\partial T})_p-\frac{R}{p}\Big]\mathrm{d}p\\&=\displaystyle\int_0^{p^0}\Big[R(B^\dagger+T\frac{\partial B^\dagger}{\partial T})+Rp(C^\dagger+T\frac{\partial C^\dagger}{\partial T})+\cdots\Big]\mathrm{d}p\end{array}$$

$$\displaystyle S^\circ_{m,id}-S^\circ_{m,re}=R\Big[(B^\dagger+T\frac{\partial B^\dagger}{\partial T})p^0+\frac{1}{2}R(C^\dagger+T\frac{\partial C^\dagger}{\partial T})(p^0)^2+\cdots \Big]~~~~~~~~~(8)$$

據經驗當標準壓力為 $$1~bar$$ 時，上式 $$p^\circ$$ 高於 $$2$$ 次方者均可忽略不計，因此 $$(8)$$ 式僅和 $$B^\dagger$$ 有關，若能求出其關係式則答案便迎刃而解。目前為止我們雖不知 $$B^\dagger$$，但是由 $$(5)$$ 式卻知道 $$B$$ 的關係式，因此只要再求出 $$B$$ 和 $$B^\dagger$$ 的關係，則 $$(8)$$ 式的解答便向前邁進一大步。

將 $$(4)$$ 式簡化如下：

$$\begin{array}{ll}\displaystyle pV_m &=\displaystyle RT[1+\frac{B}{V_m}+\frac{C}{(V_m)^2}+\frac{D}{(V_m)^3}+\cdots]~~~~~~~~~(4)\\p&=\displaystyle RT[\frac{1}{V_m}+\frac{B}{(V_m)^2}+\frac{C}{(V_m)^3}+\frac{D}{(V_m)^4}+\cdots]\end{array}$$

再將上式代入 $$(7)$$ 式

$$\begin{multline*} \displaystyle pV_m=RT\Big\{ 1+B^\dagger\Big[RT[\frac{1}{V_m}+\frac{B}{(V_m)^2}+\frac{C}{(V_m)^3}+\frac{D}{(V_m)^4}+\cdots]\Big]\\\displaystyle +C^\dagger\Big[RT[\frac{1}{V_m}+\frac{B}{(V_m)^2}+\frac{C}{(V_m)^3}+\frac{D}{(V_m)^4}+\cdots] \Big]^2+\cdots \Big\}\end{multline*}$$

$$\displaystyle pV_m=RT\Big\{1+\frac{B^\dagger RT}{V_m}+\frac{B^\dagger BRT+C^\dagger R^2T^2}{(V_m)^2}+\cdots \Big\}~~~~~~~~~(9)$$

由 $$(4)$$ 式和 $$(9)$$ 式相互比較，可得 $$B=B^\dagger RT$$，將 $$(5)$$ 式代入即可得知 $$B^\dagger$$ 和 $$a$$、$$b$$ 間的關係如下：

$$\displaystyle B=B^\dagger RT=b-\frac{a}{RT^2}$$ ，所以 $$\displaystyle B^\dagger=\frac{b}{RT}-\frac{a}{R^2T^3}$$

將此式代入 $$(8)$$ 式(只保留含 $$p^\circ$$ 的項目)

$$S^\circ_{m,id}-S^\circ_{m,re}\approx R \Big[ (B^\dagger+T\frac{\partial B^\dagger}{\partial T})p^0 \Big]\approx Rp^\circ\Big[(\frac{b}{RT}-\frac{a}{R^2T^3})+T(\frac{-b}{RT^2}+\frac{3a}{R^2T^4}) \Big]$$

$$S^\circ_{m,id}-S^\circ_{m,re}\approx \frac{2a}{RT^3}p^0~~~~~~~~~(10)$$

由 $$(10)$$ 式可知，只要知道欲求氣體物質在伯特洛方程式中的 $$a$$ 值，便能求出答案。

連結：標準狀況下理想氣體與真實氣體間的熵值差－以SO2為例(二) 

參考文獻

1. N. Levine(1988), Physical Chemistry (3rd ed.). p211~225, McGRAW-HILL Book Company.
2. 純物質相對熵的求法－以SO₂為例，高瞻計畫資源平台，http://highscope.ch.ntu.edu.tw/wordpress/?s=邱智宏
3. W. F. Giauque and C. C. Stephenson, J. Am. Chem. Soc. 1938, 60, 1389.