散度和旋度

散度和旋度 (Divergence and Curl)
國立臺灣大學物理學系 陳品全

散度 (Divergence)：

圖一、一個發散場 (A divergent field)。（本文作者陳品全繪）

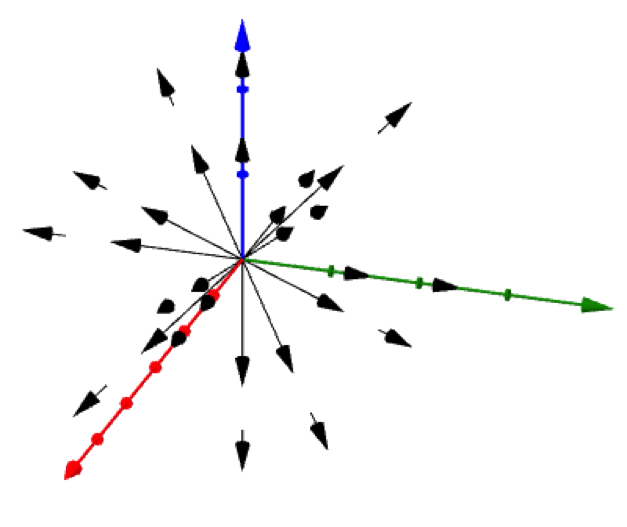
Divergence 中文譯作散度，是在形容某一個向量的發散程度為何。在三維的笛卡兒座標中，一個向量場 $$\vec{v}$$ 的散度是：

$$\displaystyle \vec{\nabla}\cdot\vec{v}\equiv\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}$$

利用散度定理 (Divergence theorem)，我們可以從另一個觀點來看散度的數學意義：

$$\displaystyle \int_V(\vec{\nabla}\cdot\vec{v})dV=\oint_{\partial V}\vec{v}\cdot d\vec{a}$$

如果要計算某個空間 $$V$$ 內向量 $$\vec{v}$$ 的散度，一個取而代之的方法是先去計算向量 $$\vec{v}$$ 通過這個空間的表面 $$\partial V$$ 的總通量為何（面積元向量 $$d\vec{a}$$ 的方向為表面上某個點的法向量，並且通常定義向外為正）。如果將這個空間縮到無限小，那麼我們則可以由散度定理重新寫出散度，為：

$$\displaystyle \vec{\nabla}\cdot\vec{v}=\lim_{V\to 0}\frac{\oint_{\partial V}\vec{v}\cdot d\vec{a}}{V}$$

旋度 (Curl)：

圖二、一個旋轉場 (A rotational field)。（本文作者陳品全繪）

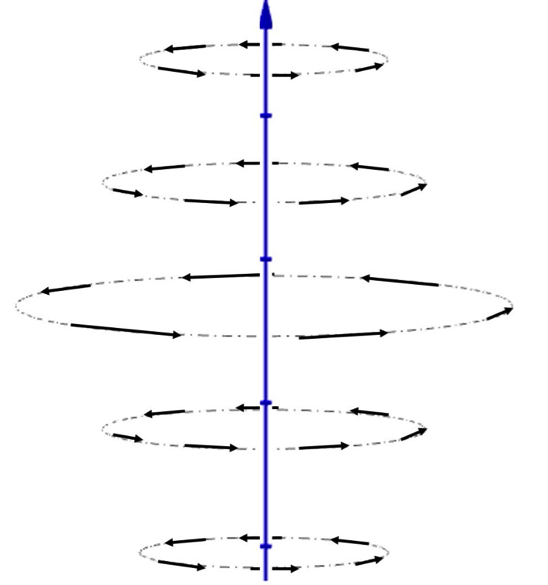
Curl 的中文譯作旋度，是在形容某一個向量旋轉的程度為何。在三維的笛卡兒座標中：

$$\displaystyle\vec{\nabla}\times\vec{v}\equiv\left(\frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z}\right)\hat{i}+\left(\frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x}\right)\hat{j}+\left(\frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\right)\hat{k}$$

利用斯托克斯定理 (Stokes’ theorem)，我們可以從另一個觀點來看旋度的數學意義：

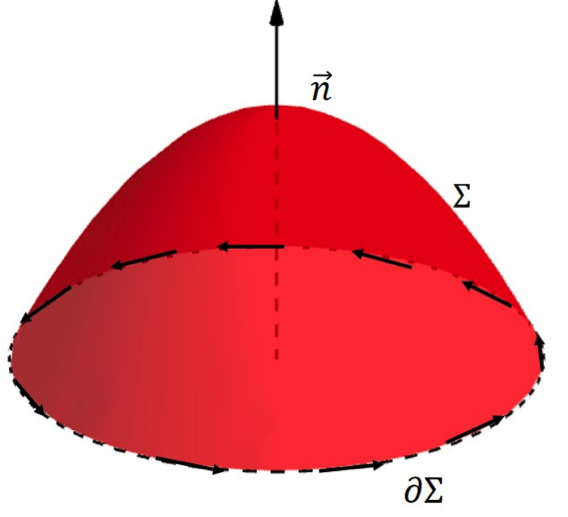
$$\displaystyle\int_\Sigma(\vec{\nabla}\times\vec{v})\cdot d\vec{a}=\oint_{\partial\Sigma}\vec{v}\cdot d\vec{s}$$

圖三、斯托克斯定理 (Stokes’ theorem)。（本文作者陳品全繪）

如果要計算某個旋度 $$\vec{\nabla}\times\vec{v}$$ 通過某個曲面 $$\Sigma$$（不一定要封閉）的總通量，那麼這個量會等於讓向量 $$\vec{v}$$ 沿著曲面 $$\Sigma$$ 的邊緣封閉曲線 $$\partial\Sigma$$ 的路徑積分。如果將面積 $$\Sigma$$ 縮到無限小，那麼我們可以利用斯托克斯定理重新寫出旋度為：

$$\displaystyle\vec{\nabla}\times\vec{v}=\lim_{A_{yz}\to 0}\frac{\oint_{\partial A_{yz}}\vec{v}\cdot d\vec{s}}{A_{yz}}\hat{i}+\lim_{A_{xz}\to 0}\frac{\oint_{\partial A_{xz}}\vec{v}\cdot d\vec{s}}{A_{xz}}\hat{j}+\lim_{A_{xy}\to 0}\frac{\oint_{\partial A_{xy}}\vec{v}\cdot d\vec{s}}{A_{xy}}\hat{k}$$

其中 $$A_{xy}$$ 為 x-y 方向上的一塊小面積，$$A_{xz}$$ 與 $$A_{yz}$$ 同理。因為旋度是具有方向性的，一般來說在笛卡兒座標需要有三個不同方向的分量才能完整描述 。

$$\vec{\nabla}\times\vec{v}$$ 是具有方向性的，它的方向朝向使 $$\oint_{\partial\Sigma}\vec{v}\cdot d\vec{s}$$ 最大化的面積法向量 $$\hat{n}$$。白話來說，就是我們可以選擇很多具有不同法向量的小迴圈當作路徑環積分的 $$\partial \Sigma$$；而在我們得到最大值的時候，我們就可以確定旋度的向量的方向為小迴圈的法向量，而 $$\vec{v}$$ 便是沿著這個法向量旋轉（右手定則：以大拇指為 $$\vec{\nabla}\times\vec{v}$$ ，其餘四指為 $$\vec{v}$$ 的方向。)

圖四、右手定則。（圖片來源：http://en.wikipedia.org/wiki/File:Right-hand_grip_rule.svg，作者：Schorschi2）

參考文獻

1. Curl — http://en.wikipedia.org/wiki/Curl_(mathematics)
2. Divergence — http://en.wikipedia.org/wiki/Divergence
3. Stokes’ theorem — http://en.wikipedia.org/wiki/Stokes’_theorem
4. Divergence theorem — Wikipedia. http://en.wikipedia.org/wiki/Divergence_theorem