蒙提霍爾問題（二）請問瑪麗蓮

蒙提霍爾問題（Monty Hall problem）(二) 請問瑪麗蓮
國立屏東高級中學數學科楊瓊茹老師

連結：蒙提霍爾問題（一）決勝21點

回顧 1990 年 9 月 9 日，瑪麗蓮‧沃斯‧薩萬特 (Marilyn vos Savant) 在《繽紛遊行》(Parade) 的「請問瑪麗蓮」專欄中，回答讀者提出的三門問題，沃斯‧薩萬特是金氏世界紀錄最高智商 \(228\) 的人，她認為選擇換的勝算比較大。為了說服讀者，她請大家想像有 \(1,000,000\) 扇門，她說：

你選擇 \(1\) 號門，而主持人知道門後有什麼，他總是避開有獎的那扇門，除了 \(777,777\) 號門外，把別的門都打開了。這時你會毫不猶豫地換到另一扇門，是吧?」

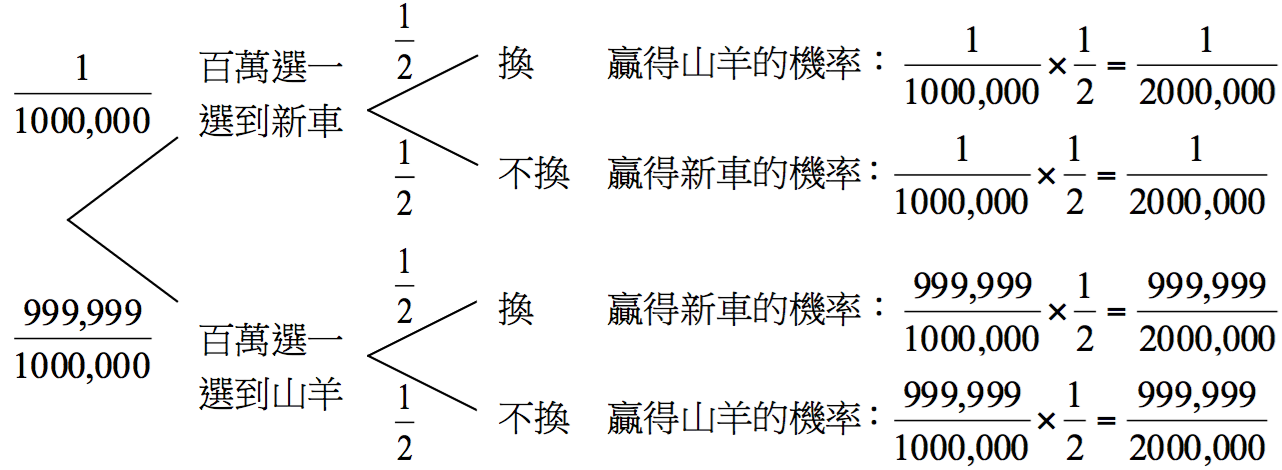
換句話說，如果你選擇 \(1\) 號門，只有 \(1/1,000,000\) 的機率猜中，而汽車在其他門後的機率是 \(999,999/1,000,000\)。當主持人打開 \(999,999\) 扇門中的 \(999,998\) 扇門，但絕對不會打開有汽車的那扇，現在拜主持人之賜，\(1\) 號門除外，只剩下的這扇門代表所有 \(999,999\) 扇門的價值，\(999,999/1,000,000\) 的機率全都集中到這一扇門。

沃斯‧薩萬特的答案是正確的，以 \(1,000,000\) 扇門為例的想法讓人耳目一新，增加門的數量卻更能看清問題的處理方式，深具啟發性。接著更進一步，我們運用貝氏定理來分析：

所以，

\(\text{P(贏得新車| 堅持不換門)}=\displaystyle\frac{1/2000,000}{1/2000,000+999,999/2000,000}=\frac{1}{1000,000}\)

\(\text{P(贏得新車| 換門)}=\displaystyle\frac{999,999/2000,000}{1/2000,000+999,999/2000,000}=\frac{999,999}{1000,000}\)

但是，沃斯‧薩萬特的回答卻引起軒然大波，大多數 \((92\%)\) 的讀者認為她是錯的，其中有近千位博士寫信給她，包括許多數學教授，其中一位教授寫道：

你搞砸了！我解釋給你聽：如果已經知道一扇門是輸的，這就改變了選擇剩下兩扇門的機率–沒有任何一扇門會比另一扇門的機率更高，也就是每扇門都是的機會。身為數學家，我對一般大眾欠缺數學知識甚感憂心。幫幫忙吧，承認你的錯誤，未來更謹慎一些。

抨擊沃斯‧萬特斯的信件不斷地寄來，甚至有的語帶諷刺地批評：

你在鬼扯！……，這個國家的數學文盲已經夠多的了，我們不需要世界上智商最高的人再來幫倒忙。真丟臉！

面對讀者的圍攻，這一次沃斯‧萬特斯用表格完整列出所有可能的結果：

她說這張表顯示出：「你若換一扇門，贏的機會是 \(2/3\)，而輸的機會是 \(1/3\)；但是如果你不換門，則贏的機會只有 \(1/3\)。」此一表格充份顯現樣本空間的威力，也讓批評的人後悔不已。

其實，無需任何機率法則的運算，只要反過來想，如果你選擇換門，那麼一開始選到山羊才會贏，所以贏的機率是 \(2/3\)；如果選擇不換門，那麼一開始選中新車才會贏，所以贏的機率是 \(1/3\)。

沃斯‧萬特斯被稱為「全世界最聰明的人」當之無愧。至於讓大多數人都出槌的「蒙提霍爾問題」，葛登能(Mart Gardner)於《科學美國人》中給了最佳的注解：「絕妙又惱人的小問題」、「數學中還沒有其他哪個領域，比機率理論更容易令專家出錯。」

參考資料：

1. 曼羅迪諾著、胡守仁譯(2012)，《醉漢走路–機率如何左右你我的命運和機會》，台北：天下遠見出版社。
2. Bruce Schechter著、曾蕙蘭譯(1999)，《不只一點瘋狂–天才數學家艾狄胥傳奇》，台北：先覺出版社。
3. Paul Hoffman著、米緒軍、張曉燕、繆衛東譯(2001)，《數字愛人–數學奇才艾狄胥的故事》， 台北：臺灣商務印書館。