多項式除法
多項式除法 (Polynomial Quotients and Remainders)
國立中央大學數學系單維彰副教授責任編輯
多項式的「元」具備如實數一般的運算性質,但是多項式本身的運算性質卻像正整數:兩個多項式相除,會得到商式並產生餘式。類似於正整數的除法原理,若多項式 $$P$$、$$K$$、$$Q$$、$$R$$ 滿足 $$\mathrm{deg}~R <\mathrm{deg}~K$$ 且 $$P=QK+R$$,例如 $$x^2=(x+1)(x-1)+1$$ 則它們也可以寫成多項式除法形式:
$$P\div{K}=Q…R$$
例如 $$x^2\div(x-1)=(x+1)…1$$。我們稱 $$P$$ 為被除式、$$K$$ 為除式、$$Q$$ 為商式、$$R$$ 為餘式,而 $$P=QK+R$$ 和 $$P\div{K}=Q…R$$的等價關係,稱為多項式的除法原理。
類似多項式的加、減、乘可以寫成直式,多項式相除也有直式,稱為長除法;我們以 $$x^2$$ 除以 $$x-1$$ 為例示範如下:
在得到了紅色的商式與綠色的餘式之後,我們可以將答案記成
$$x^2\div(x-1)=(x+1)…1$$
同樣地,我們也能使用分離係數法,以 $$6x^3-x+3$$ 除以 $$2x-1$$ 為例示範如下:
我們一樣可以將除法記錄為 $$\displaystyle(6x^3-x+3)\div(2x-1)=(3x^2+{\frac{3}{2}}x+\frac{1}{4})…\frac{15}{4}$$。
根據除法原理,如果 $$P\div{K}=Q…R$$ 則 $$P-R={QK}$$。
例如 $$\displaystyle 6x^3-x+3-{\frac{15}{4}}=(3x^2+{\frac{3}{2}}x+\frac{1}{4})(2x-1)$$。
如果餘式是 $$0$$,亦即 $$P\div{K}=Q$$ 或 $$P=QK$$ ,則 $$Q$$ 和 $$K$$ 都稱為 $$P$$ 的因式。
例如 $$\displaystyle 3x^2+\frac{3}{2}x+\frac{1}{4}$$ 和 $$2x-1$$ 都是 $$\displaystyle 6x^3-x-\frac{3}{4}$$ 的因式。
顯然,如果 $$P=QK$$ 則 $$P\div{K}=Q$$,這是多項式的乘除互逆性質。
將多項式 $$P$$ 寫成因式相乘的形式,如 $$P=QK$$,稱為 $$P$$ 的因式分解。因為非零實數也就是零次多項式,所以多項式總有(無聊的)因式分解,例如 $$\displaystyle x^2+1=\frac{1}{5}(5x^2+5)$$。
同理,因式分解並不唯一,例如
$$\displaystyle x^2-1=(x+1)(x-1)=(2x+2)(\frac{1}{2}x-\frac{1}{2})$$。
多項式除法中,若除式正好為 $$x-c$$ 的形式,則有一種更簡便的方法可以做除法,稱為綜合除法。讓我們觀察 $$(x^3-2x^2-x-4)\div(x-3)$$,在將之以分離係數法表示後,可以發現有許多數字都在重覆,在下方用相同顏色標記:
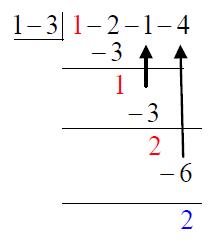
如我們所知,餘數存在於長除法的最後一層,而粉紅色與綠色的部分其實也表現出了商式,因此我們可以省略商式,也省略長除法中重覆的數字,如下:
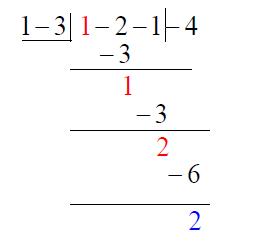
此時紅色為商式,藍色為餘式。將長除法中第二層、第三層的數字全部合併上來,可以進一步縮減直式的高度,如下:
由於綜合除法僅適用於$$x-c$$ 的形式,$$x$$ 項的係數 $$1$$ 也可以省略。綜合所有的省略和合併,我們便能寫成以下形式:
其中紅色的部分是商式,藍色是餘式(此時的餘式必為一個實數)。我們又注意到,在以上計算過程中,總是重複地做 $$a-(-c)b$$ 形式的計算,例如第二行做 $$(-2)-(-3)$$,第三行做 $$(-1)-(-3)$$,第四行做 $$(-4)-(-6)$$。既然如此,何不做 $$a+cb$$ 就好了?
重新整理以上的發現,就是綜合除法,示範如下。我們先列出被除式的係數(降冪排列,缺項補零),例如將 $$x^3-2x^2-x-4$$ 的係數列為 $$1~~-2~~-1~~-4$$;如果除式是 $$x-c$$,將 $$c$$(而不是 $$-c$$)寫到式子的右側,例如當除式是 $$x-3$$,寫 $$3$$ 在右側。畫一條折線隔開:
將首項係數抄到下層:
乘以右邊的 $$3$$,寫在第二行的中層;將上、中層的兩數相加寫到下層:
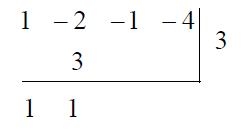 再乘以右邊的 $$3$$,寫在第三行的中層;將上、中層的兩數相加寫到下層:
再乘以右邊的 $$3$$,寫在第三行的中層;將上、中層的兩數相加寫到下層:
再乘以右邊的3,寫在第四行的中層;將上、中層的兩數相加寫到下層:
則下層的最後一個數就是餘式,而其他數則是降冪排列的商式係數。所以商式是 $$x^2+x+2$$,餘式是 $$2$$。




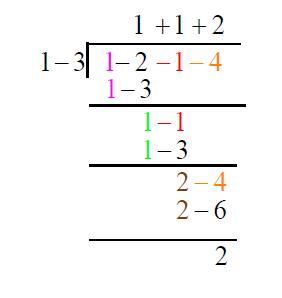
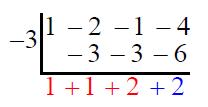
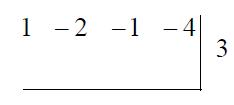
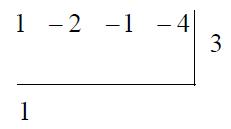
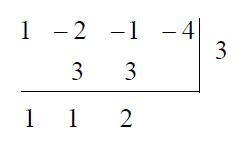
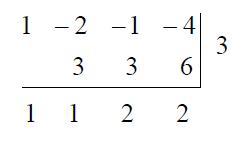
 前一篇文章
前一篇文章 下一篇文章
下一篇文章 惠更斯 (Christiaan Huygens) 專題
惠更斯 (Christiaan Huygens) 專題  泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2))  海芭夏 (Hypatia of Alexandria)
海芭夏 (Hypatia of Alexandria) 

講得很清楚! 推一個!