賭金分配問題 (The Problem of Division of the Stakes)(二)

賭金分配問題 (The Problem of Division of the Stakes)(二)
國立屏東高級中學數學科楊瓊茹老師

參考 賭金分配問題(一)

在費馬的解法中，他考慮再比賽三局所有可能的情況為(\(A\)表甲勝、\(B\)表乙勝)：

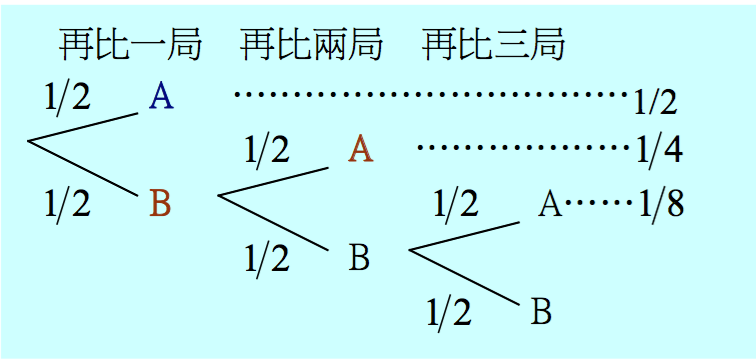
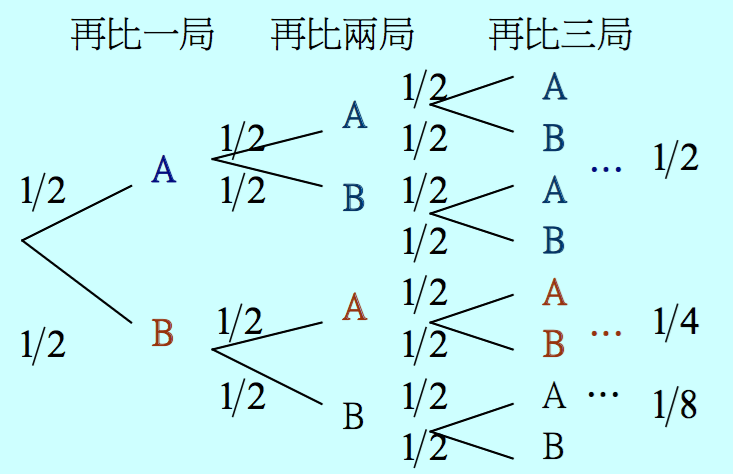
不過，還要比 \(3\) 局的計算方式似乎有些奇怪，因為在甲已勝 \(5\) 局的優勢下，AAA這三場中根本就不必再比最後兩局、BAB中也不用比最後一局。事實上，我們在甲得 \(6\) 勝時比賽就結束，這兩個想法乍看之下顯然有些不同，但其實是相同的。因為不管甲 \(6\) 勝時是否還打了後面那幾局，那些結果“依然存在”(參見樹狀圖)。

又例如：投擲一枚公正的硬幣，假設任何時候你只要擲出一個正面(\(A\))就算贏，擲兩次的可能結果有 \(2^2\) 種：

在AA、AB的情形中，是不必擲第二次的。可是那些結果“依然存在”，\(4\) 個完整的結果中有 \(3\) 個包含了 \(A\)，你贏的機率仍是 \(\frac{3}{4}\)。

不過，當比賽的局數太多時，使用費馬的方法列出所有的結果十分繁瑣不便。此時，巴斯卡展示一套有系統的方法。比賽 \(3\) 局的 \(8\) 種情況，直接由巴斯卡三角形圖表讀出，甲贏 \(0\)、\(1\)、\(2\) 或 \(3\) 局的方法數分別為：\(1\)、\(3\)、\(3\)、\(1\) 所以，甲贏得賭注有 \(7\) 種方式、乙只有 \(1\) 種。

除此之外，他還給出公式解，用現代符號翻譯如下：

假設甲再贏 \(r\) 局就可以獲得賭金，而乙還要贏 \(s\) 局才可以獲得賭金，\(r\) 和 \(s\) 至少是 \(1\)。如果比賽此時終止，則賭金應當如此分配：甲獲得的賭金與全部的賭金之比例為 \(\sum\limits_{k = 0}^{s – 1} {C_k^n} :{2^n}\)，其中 \(n=r+s-1\)。

考慮再比賽 \(n\) 局，所有的可能情形總共有 \(2^n\) 種，

甲贏 \(0\)、\(1\)、\(2\)、\(3\)、…或 \(n\) 局的方法數分別為 \({\rm{C}}_0^n,{\rm{C}}_1^n,{\rm{C}}_2^n,…,{\rm{C}}_n^n\)。

所以，甲至少贏 \(r\) 局的情形有 \({\rm{C}}_r^n + C_{r + 1}^n + C_{r + 2}^n +\cdots+ C_n^n\) 種，又 \(C_k^n = C_{n – k}^n\)，

故 \({\rm{C}}_r^n + C_{r + 1}^n + C_{r + 2}^n +\cdots+ C_n^n = {\rm{C}}_{{\rm{s – 1}}}^{\rm{n}} + C_{s – 2}^n + C_{s – 3}^n +\cdots+ C_0^n = \sum\limits_{k = 0}^{s – 1} {{\rm{C}}_k^n} \)。

因此，甲獲得的賭金與全部賭金之比為 \(\sum\limits_{k = 0}^{{\rm{3}} – 1} {C_k^{\rm{3}}} :{2^{\rm{3}}} = {\rm{C}}_{\rm{0}}^{\rm{3}} + {\rm{C}}_{\rm{1}}^{\rm{3}} + {\rm{C}}_{\rm{2}}^{\rm{3}}{\rm{:}}{{\rm{2}}^{\rm{3}}} = {\rm{7:1}}\)。由此可見，巴斯卡三角形除了展現二項式展開式的係數，更重要的貢獻是應用在賭金分配問題的一般化解法。

參考文獻

1. Katz, Victor J. (1993) ,《A history of mathematics.》, Harper Collins College Publishers.
2. 曼羅迪諾著、胡守仁譯(2012)，《醉漢走路-機率如何左右你我的命運和機會》，台北：天下遠見出版社。
3. http://commons.wikimedia.org/wiki/File:TrianguloPascal.jpg