和算中的行列式(1)：創立者關孝和
（Determinants in Wasan (1): Seki Takakazu, the originator）
國立臺南第一高級中學林倉億老師

日本江戶時代 (1603-1867，即德川幕府時代) 的數學家在吸納了來自中國的數學知識後，獨立發展出許多新理論及新算法，後人就將這時期的數學稱為「和算」，這時期的數學家就稱為「和算家」。在這些和算家中，最突出也最具代表性的一位，就是關孝和。他不但被後世稱為「算聖」，更是世界上最早提出行列式的人之一。

我們對關孝和的生平所知不多，就連他是不是在1642年出生的，現在仍有爭議；不過，1708年離開人世，這殆無疑問。關孝和本姓內山，過繼給一位關姓武士後才改姓。關孝和是甲府宰相德川綱重及其子德川綱豐的家臣，擔任「勘定吟味役」的職位，相當於會計總管的職務。在德川綱豐成為德川將軍的養子後，關孝和也就成為幕府直屬的武士，官至「御納戶組頭」，負責幕府的用具。總而言之，關孝和在官途上並沒有什麼特別之處，就是以家臣的身份，為領主奉獻心力。

相較於平凡的仕途，關孝和在數學上的成果就更顯得非凡燦爛了。 Continue reading →

西方行列式的發展：貝祖的研究
(The Development of Determinants in West: Bézout’s Work)
國立臺南第一高級中學林倉億老師

萊布尼茲雖然可被視為西方第一個做出行列式相關研究的人，但他對後來的發展影響並不大（參閱本網站〈行列式的濫觴：萊布尼茲 (1)〉一文）。真正廣為人知的，是克拉瑪對聯立方程組的研究，以其名命名的「克拉瑪公式」更是現行高中教材中的內容。關於克拉瑪在行列式方面的工作，也請參閱本網站的文章：〈克拉瑪公式(2)：克拉瑪的公式〉，筆者在此不再贅述。但也要提醒讀者，在克拉瑪之前，蘇格蘭愛丁堡大學的數學教授麥克勞林已提出相當於二元與三元聯立方程組的「克拉瑪公式」，本網站〈各式聯立方程組的程序性解法(1)：麥克勞林與卡丹諾〉一文對此有簡短的介紹。本文要介紹的，是法國數學家艾帝安‧貝祖 (Étienne Bézout, 1730-1783) 於1764年提出的成果。 Continue reading →

獨立事件 (Indenpent Event)
國立蘭陽女中陳敏晧教師

已知 \(A\) 與 \(B\) 為樣本空間中的兩個事件，

若 \(P(A\cap B)=P(A)\cdot P(B)\)，則稱 \(A\) 事件與 \(B\) 為獨立事件；
若 \(P(A\cap B)\ne P(A)\cdot P(B)\)，則稱 \(A\) 事件與 \(B\) 為相關事件。

另一種解釋獨立事件的方式為當 \(B\) 事件的發生並不影響事件 \(A\) 發生的機率，
即 \(P\left( {A\left| B \right.} \right) = P\left( A \right) \Leftrightarrow \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = P\left( A \right) \Leftrightarrow P\left( {A \cap B} \right) = P\left( A \right)P\left( B \right)\)。

若已知事件 \(A\) 與 \(B\) 為獨立事件，則

1. \(A\) 與 \(B’\) 為獨立事件。其中 \(B’\) 為之補集合。
2. \(A’\) 與 \(A\) 為獨立事件。
3. \(A’\) 與 \(B’\) 為獨立事件。

證明：

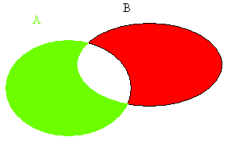
(1) \(\begin{array}{ll}P\left( {A \cap B’} \right) &= P\left( A \right) – P\left( {A \cap B} \right) = P\left( A \right) – P\left( A \right)P\left( B \right) \\&= P\left( A \right) \cdot \left( {1 – P\left( B \right)} \right) = P\left( A \right)P\left( {B’} \right)\end{array}\)，得證。參閱圖一。

圖一

Continue reading →

如何計算紅球先取完的機率？
(How to calculate the probablity of taking all the red balls first ?)
國立蘭陽女中陳敏晧教師

排列組合教學過程中，有一個值得討論的議題：「如何計算紅球先取完的機率？」
先從兩種不同顏色球的討論開始：

例1：

袋中有三個紅球與兩個白球，今從袋中每次取一球，取後不放回，請問紅球比白球先取完的機率？

解法：

因為紅球先取完，所以，最後一球必定是白球，因此，
\( P(\text{紅球比白球先取完})= \displaystyle\frac{{\frac{{4!}}{{3! \times 1!}}}}{{\frac{{5!}}{{3! \times 2!}}}} = \frac{2}{5} = \frac{2}{{3 + 2}} = \frac{W}{{R + W}}\)，
其中 \(R\) 代表紅球的個數，\(W\) 代表白球的個數。

接著，透過排容原理(Inclusion–exclusion principle)或取捨原理，

如下圖一與圖二所示，可以將問題延伸。 Continue reading →

期望值(Expected Value)
臺北市立第一女子中學數學科蘇俊鴻老師

如果想要粗略估計隨機變數 \(X\) 的大小，期望值 \(E(X)\) 是一個常用的代表。
而期望值定義是：

若隨機變數 \(X\) 的機率分布如下
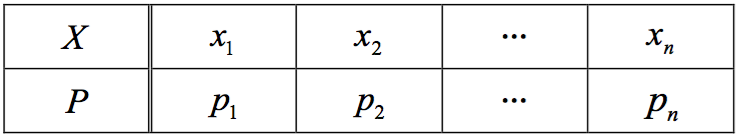則隨機變數 X 的期望值 \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + \cdots + {x_n}{p_n} = \sum\limits_{i = 1}^n {{x_i}{p_i}} \)

換言之，隨機變數 \(X\) 的期望值是 \(X\) 的所有可能值的加權平均數。 Continue reading →

布里格斯的《對數算術》與對數表的製作(III) (Briggs’ Arithmetica Logarithmica and the creation of logarithmic table, part 3)
臺北市立西松高中蘇惠玉教師

連結：布里格斯的《對數算術》與對數表的製作(II) 

《對數算術》第 $$8$$ 章

在第 $$6$$、$$7$$ 兩章中，布里格斯為了處理連續開方，需要花費相當大的時間與精力在作開方的計算上。因此，他需要有個方法可以幫助他減少計算量，他將使用的方法寫在第 $$8$$ 章，稱為差分法（difference method）。

布里格斯在作開方時，發現一個 $$1$$ 點多的數開方，小數部分的值幾乎是原本的二分之一，藉由這樣的觀察，他利用與一半的「差距」，用一系列的演算法求得連續開方的下一項，以減少龐大的開方工作量。

首先，布里格斯選擇作連續幾次平方根後，小數點後面有 $$3$$ 或 $$4$$ 個 $$0$$ 之數為起始值，

分別計算 $$B,C,D,E,F$$ 等欄位的值，他們之間的關係如下：

他從 $$6^9/10^7=1.0077696$$ 開始作連續開方，其中 $$1+A_n$$ 表示作第 $$n$$ 次開方的值，

並依序計算相對應的 $$B,C,D,E,F$$ 等欄位的值。 Continue reading →

布里格斯的《對數算術》與對數表的製作(II) (Briggs’ Arithmetica Logarithmica and the creation of logarithmic table, part 2)
臺北市立西松高中蘇惠玉教師

連結：布里格斯的《對數算術》與對數表的製作(I) 

《對數算術》第 $$5$$～$$7$$ 章

第 $$5$$ 章到第 $$8$$ 章為計算以 $$10$$ 為底的對數的主要方法。在第 $$5$$ 章中所提的方法，布里格斯將它歸功於納皮爾。他以 $$\log 5$$ 與 $$\log 7$$ 為例，說明小一點的質數如何求其對數值。考慮 $$\log 2$$，先計算 $$2$$ 的次方，並標明其位數。

為了使對數值精確到小數點後第 $$14$$ 位，布里格斯計算到了 $$2^{10^{14}}$$；不過，他也不是每個都算，而是以四個數一組，每次都計算次方為 $$2\times 10^k,4\times 10^k,8\times 10^k,10\times 10^k$$ 的四個數的位數，如下圖一。在計算位數時，布里格斯並沒有將每個數完整算出後計算，他利用了下面這個性質：如要計算兩數相乘後的位數，考慮這兩數的首幾位數字，相乘後的位數不是兩者位數相加，就是兩者位數相加再減 $$1$$，如下圖二。 Continue reading →

布里格斯的《對數算術》與對數表的製作(I) (Briggs’ Arithmetica Logarithmica and the creation of logarithmic table, part 1)
臺北市立西松高中蘇惠玉教師

在高中數學課程中，對數觀念的學習與應用是相當重要的一個單元。不過，在學習的過程中，課程雖然著重在觀念的理解，與對數表的應用，卻沒有明白地告訴學生 $$\log 2,\log 3$$ 等等的對數值，到底是怎麼算出來的。因此，學生對此單元的學習容易因為一知半解的情況，而顯得成效不彰。

接下來這一系列的相關文章，將說明布里格斯（Henry Briggs, 1561~1630）在他的《對數算術》（Arithmetica Logarithmica）一書中，所用來建造以 $$10$$ 為底的對數表之幾種方法，並希望能將這些方法應用在目前的數學課堂的學習上，讓學生可以了解或親自動手算算這些常用對數的值。 Continue reading →