東亞第一本微積分課本（The First Calculus Textbook in East Asia）
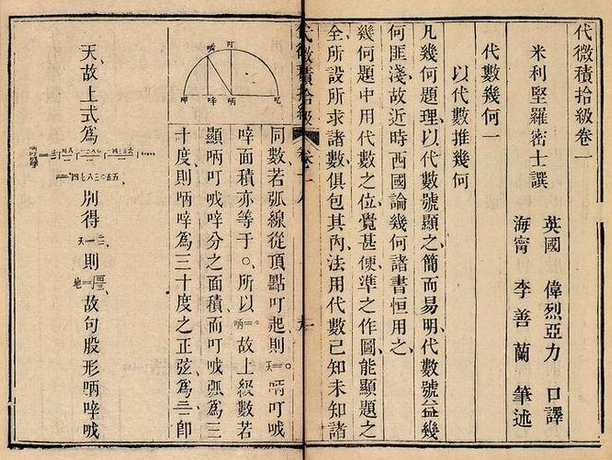
國立臺灣師範大學數學系洪萬生教授/國立臺灣師範大學數學系洪萬生教授責任編輯

中國清朝數學家李善蘭  (1811-1882)  在 1859 年與英國傳教士偉烈亞力 (Alexander Wylie) 合作，翻譯了羅密士 (Elias Loomis, 1811-1899) 的 Elements of Analytical Geometry and of the Differential and Integral Calculus (1850)，中譯版書名命為「代微積拾級」，強調本書依序講述「代（數）」（解析幾何）、「微（分）」與「積（分）」，「拾級」而上。

事實上，李善蘭在譯序中即指出：「羅君密士合眾之天算名家也。取代數、微分、積分三術合為一書，分款設題，較若列眉，嘉惠後學之功甚大。……是書先代數次微分、次積分，由易而難，若階級之漸升。譯既竣，即名之曰代微積拾級。」

此外，偉烈亞力也在譯序中，點出此書中譯的脈絡意義：「微分積分，為中土算書所未有，然觀當代天算家，如董方立氏、項梅侶氏、徐君青氏、戴鄂士氏、顧尚之氏，暨李君秋紉，所著各書，其理有甚近微分者，因不用代數式，或言之甚繁推之甚難，今特偕李君譯此書，為微分積分入門之助。」

上引文提及之天算家依序為董祐城、項名達、徐有壬、戴煦、顧觀光以及李善蘭，都是十九世紀中國清代數學名家。不過，他們的共同「不足」，顯然如偉烈亞力所說的，由於「不用代數式」，因此，才會顯得「言之甚繁，推之甚難」，從而可見解析幾何這一理論系統的不可或缺。

這或許也解釋了何以偉烈亞力推薦此書之中譯，因為本書之前九卷，即是解析幾何之內容，而這當然是微積分的先備知識。不過，在本書中，英文原文中的 analytical geometry（解析幾何）一概翻譯為「代數幾何」。

其次，微分有七卷（卷十到十六）。其中，羅密士主要運用微係數 (differential coefficient) 來表示我們今日所謂的導數 (derivative)：「函數與變數之比例，俱謂之微分，用ㄔ號記之。如戌 \(=\) 天三，則得比例ㄔ天 : ㄔ戌 :: 一 : 三天二。ㄔ天、ㄔ戌為天與戊之微分。後皆仿此。用表天與戌之變比例，以一、四兩率相乘，二、三兩率相乘則得ㄔ戌 \(=\) 三天二ㄔ天，此顯函數戌之變比例，等於三天乘變數天之變比例，以ㄔ天約之得ㄔ天/ㄔ戌 \(=\) 三天二。此顯變數之變比例約函數之變比例，等於函數之微係數也。」

上述引文有必要解釋或註解一下。李善蘭與偉烈亞力將函數 \(u=f(x)\) 中的 \(u\) 記作戌，\(x\) 記作天；\(u=x3\) 記作戌 \(=\) 天三；微分記號 \(d\)「翻譯」為漢字記號ㄔ，顯然他擷取了「微」字的部首「ㄔ」。因此，「ㄔ天 : ㄔ戌 :: 一 : 三天二」即相當於「\(dx : du = 1 : 3\times 2\)」。還有，由於當時的分數之分子、分母之位置，恰好與目前習慣相反，亦即分子置於下，分母置於上，於是，\(du/dx\) 才會譯為ㄔ天/ㄔ戌。

根據上述引文，針對任何一個函數 \(y=f(x)\) 而言，羅密士先求出 \(dy=f(x)dx\)，然後，再得到 \(dy/dx＝f(x)\)。如此一來，他可以避開導數之定義中，\([f(x+h)-f(x)]/h\) 之分子與分母同時趨近於零的論證難題。後者不待外爾斯特拉斯（Karl Weierstrass）所領導的柏林學派之分析算術化 (arithmetization of analysis)，而提出極限的 \(\varepsilon-\delta\) 定義，是無法解決的。在1872年，外爾斯特拉斯的徒弟漢內（Heine）在老師的上課筆記中，總結了微積分理論的嚴密化工作。

羅密士擁有LL. D（法學博士），出版這一本教科書時，正擔任紐約市立大學的數學與自然哲學教授 (Professor of Mathematics and Natural Philosophy, the University of the City of New York)。不過，當時美國仍然是國際數學社群的邊陲地帶，大學教師的主要著作都是類似微積分這種大學教科書。

儘管如此，本書英文原著迄至1859年為止，已經出版到第10版，足見它相當受到大學教師的青睞。羅密士也承認本書「並非為了數學家、也不是為了那些擁有特殊天分或是數學的愛好者，而是為廣大中等資質的大學生而寫。」這或許也是本書英文原版暢銷的原因之一吧。其實，就今日標準而言，本書除了例題比較「老套」之外，體例與內容還是蠻適合充當非數學、物理主修的大學生之微積分教材。

本書還有一個特色，那就是：相對於七卷的微分內容，積分只有兩卷！〈積分一總論〉一開始內容如下：「積分為微分之還原，其法之要在識別微分所由生之函數，如已得天二之微分為二天ㄔ天，則有二天ㄔ天即知所由生之函數為天二，而天二即為積分。已得微分所由生之函數為積分，而積分或有常數附之，或無常數附之，既不能定，故式中恆附以常數，命為口丙，口丙或有同數或為 \(0\)，須攷題乃知。來本之視微分若函數諸小較之一，諸小較并之，即成函數，故微分之左係一禾字，指欲取諸微分之積分也。如下式 禾二天ㄔ天 \(=\) 天 \(+\) 口丙。來氏說，今西國天算家大率不用，而惟用此禾字取其一覽了然也。」

在上述引文中，李善蘭與偉烈亞力將Leibniz翻譯為「來本之」，同時，積分記號 \(\int\)（一個拉長的S）則譯為「禾」，它取自「積分」的積字之偏旁部首「禾」。羅密士指出：儘管「今西國天算家大率不用」「來氏說」(philosophy of Leibniz)，「而惟用此禾字」，「取其一覽了然也」。在這個脈絡中，羅密士未曾獨立地定義定積分 (definite integral)，而是通過不定積分 (indefinite integral) 來定義，這省掉了定義定積分的麻煩，值得稱道。

---

參考書目

1. Horng, Wann-Sheng (1991). Li Shanlan: The Impact of Western Mathematics over China in the late 19th Century. Ph. D. Thesis, City University of New York.
2. Loomis, Elias (1859). Elements of Analytical Geometry and of the Differential and Integral Calculus. New York: Harper & Brothers, Publishers.
3. 羅密士撰（偉烈亞力口譯，李善蘭筆述）(1859).《代微積拾級》，上海：墨海書館。

《筭數書》：超過兩千年的漢簡數學書（Suan Shu Shu: Han Bamboo Math Text over Two Thousand years）
國立臺灣師範大學數學系洪萬生教授/國立臺灣師範大學數學系洪萬生教授責任編輯

目前在全世界的古代出土文物中，超過兩千年的數學文本可以說是鳳毛麟角。近二十年來，在中國發現的秦簡《數》與漢簡《筭數書》，就是極珍貴的例外，非常值得我們一起來分享這些世界文化遺產的價值與意義。在本文中，我們只介紹《筭數書》。

Continue reading →