2005年1月14日，歷經了七年的行星際旅程，歐洲太空總署的惠更斯號 以降落傘登陸在土星最大衛星─泰坦，完成一次歷史性的著陸。

惠更斯〈1629-1695〉，荷蘭物理學家、天文學家和數學家， 土衛六的發現者，主要的功績是研究了「擺動的規律」，發明了擺鐘；光的波動理論的創立者；對動力學作出最早的貢獻，包括建立圓周運動的數學理論。他還發現了獵戶座大星雲和土星光環的真實形狀， 10年前登陸泰坦的惠更斯號便是以他命名。 Continue reading →

泰勒多項式(2) （Taylor Polynomials(2)）
臺北市立第一女子高級中學蘇俊鴻老師

連結：泰勒多項式(1) （Taylor Polynomials(1)）

在〈泰勒多項式(1)〉中，我們提到：

任意實係數 \(n\) 次多項式 \(f(x)\)，定能表成 \(f(x)\) 在 \(x=a\) 處的泰勒多項式

\(\begin{multline*}\displaystyle f\left( x \right) = f\left( a \right) + \frac{{f’\left( a \right)}}{{1!}}\left( {x – a} \right) + \frac{{f”\left( a \right)}}{{2!}}{\left( {x – a} \right)^2} + \frac{{f”’\left( a \right)}}{{3!}}{\left( {x – a} \right)^3} \\+\cdots+\frac{{{f^{\left( n \right)}}\left( a \right)}}{{n!}}{\left( {x – a} \right)^n}\end{multline*}\)

這個定理對於我們回頭解決多項式的問題，或是研究多項式的性質很有幫助，本文的目的，就是提出泰勒多項式的幾個應用。 Continue reading →

泰勒多項式(1) （Taylor Polynomials(1)）
臺北市立第一女子高級中學蘇俊鴻老師

請考慮下面的問題：

已知多項式函數 \(f(x)=-x^3+5x^2-8x+4\)，求 \(f(0.99)\) 的值（四捨五入取到小數點以下第二位）。

儘管將 \(x=0.99\) 代入，即可求出函數值。
但 \(f(0.99) =- {(0.99)^3} + 5 \times {(0.99)^2} – 8 \times (0.99) + 4\) 繁複計算過程令人卻步。

因此，處理這類問題，通常採取下面的作法

• 步驟一：將 \(f(x)\) 表示成 \(f(x) = a + b(x – 1) + c{(x – 1)^2} + d{(x – 1)^3}\)，
  計算出 \(a,b,c,d\) 各值。此題的結果 \(a=0,b=-1,c=2,d=-1\)
• 步驟二：將 \(x=0.99\) 代入，即可估取近似值。

以上題為例，由步驟一知，\(f(x) =- (x – 1) + 2{(x – 1)^2} – {(x – 1)^3}\)。所以，

\(\begin{array}{ll} f(0.99) &=-(0.99-1)+2\times{(0.99-1)^2}-{(1-0.99)^3}\\&=-(0.01)+2\times{(0.01)^2}-{(0.01)^3}\\&\approx -(0.01)=-0.01\end{array}\)

由步驟二的數值計算來看，應能推敲步驟一將原多項式改寫成以 \((x-1)\) 的冪次方升冪排列的多項式之用意。不過，進一步思考，上述解法正表明：當 \(1-\varepsilon\le x\le 1+\varepsilon\)，其中的 \(\varepsilon\) 為足夠小的正數時，有 \(f(x)\approx -(x-1)\)。 Continue reading →

貝葉斯和貝氏定理(3)（Thomas Bayes and Bayes’ Theorem (3)）
臺北市立第一女子高級中學蘇俊鴻老師

連結：貝葉斯和貝氏定理(2)

接著，我們來看貝葉斯如何求出 \(P(F)\) 和 \(P(E\cap F)\)。他用了一個頗為獨特的想法，據以建立機率模型進行計算。如圖一，考慮水平擺放一個正方形的桌面或平面 \(ABCD\)，將球 \(O\) 或 \(W\) 拋向桌面，並假設它們落在桌面上任何相等區域內的機率相同。

這時，假設球 \(W\) 先拋，過落點畫一條直線 \(ot\) 平行 \(AD\)，分別交 \(CD\) 與 \(AB\) 於 \(t\) 和 \(o\)。接著，球 \(O\) 被拋擲 \(p+q=n\) 次，如果它一次單獨拋擲中落在 \(AD\) 和 \(ot\) 之間，稱為在一次試驗中發生了事件 \(M\)。

圖一

Continue reading →

貝葉斯和貝氏定理(2)（Thomas Bayes and Bayes’ Theorem (2)）
臺北市立第一女子高級中學蘇俊鴻老師

連結：貝葉斯和貝氏定理(1)

在說明貝葉斯的論文〈《機率論》中一個問題的解決〉(An Essay towards Solving a Problem in the Doctrine of Chances)內容之前，先來交待一下當時機率論的發展情形。由於法國貴族默勒(Chevalier de Mere)請教巴斯卡(Blaise Pascal, 1601-1665)骰子擲點及賭金分配等問題，引發巴斯卡與費瑪(Pierre de Fermat, 1601-1665)兩人書信討論解決，奠立了機率論的基礎。

1655 年，荷蘭數學家惠更斯(Christiaan Huygens, 1629-1695)走訪巴黎，得知巴斯卡與費瑪兩人討論的問題，引發興趣，進而延伸討論，1657年出版一本小冊子《論機率博奕的計算》(On the Calculations in Games of Chance)。到十八世紀初，該書一直都是機率論入門的著作。

而伯努利(Jakob I. Bernoulli, 1654-1705)在惠更斯的基礎上，因應當時對於保險風險評估等實際的需求，討論機率與各種實際問題的結合。在他死後8年，出版的《猜度術》(Ars Conjectandi, 1713)成為機率論重要的著作。今日我們所知的大數法則、二項分佈等概念，均在書中可見。伯努利認為任意給定誤差範圍，只要實驗次數足夠多，希望產生的結果總數與實驗總數的比值和理論值 \(p\) 的差距就會在給定範圍內。依此，就能推估觀測的次數。不過，他對二項分佈的近似公式取得不夠好，無法應用於實際情形上。

這個工作後來就由棣美弗完成。1733年棣美弗發展出我們現在所說的常態曲線，作為二項分佈的近似，改善伯努利所需觀測次數之估計(高斯及拉普拉斯後來又重新發現)。棣美弗將此法收入1738和1756年再版的《機率論》中(此書於1718年初版)。由貝葉斯論文的標題〈《機率論》中一個問題的解決〉，我們得知他的工作奠基於棣美弗的成果上。文章開頭，便表明他想解決的問題是給定某未知事件(指發生的機率未知)發生與未發生的次數，求在一次試驗中發生的機率值介於兩個指定機率值之間的可能性(機率)。

以現在的符號表示，令 \(X\) 為 \(n\) 次試驗中事件發生的次數，\(x\) 表事件在一次試驗中發生的機率值，\(r,s\) 為指定的機率且 \(r<s\)。那麼，貝葉斯所求問題即為

\(P(r<x<s|X)=?\)

貝葉斯採取公理化的體系，先給出定義，再提出命題，其中最重要的兩個命題是：

• 命題3
  兩個相繼發生的事件機率是一個比率，它由第一事件發生的機率，以及在第一事件發生的條件下第二事件的機率複合而成。
• 命題5
  若有兩個相繼發生的事件，已知第二事件的機率為 \(\frac{b}{N}\)，兩者都發生的機率為 \(\frac{P}{N}\)。由於第二事件已經發生，據此我猜想第一事件也會發生，且它的機率無疑是 \(\frac{P}{b}\)。

令 \(E\) 表示第一事件，\(F\) 表示第二事件。那麼，命題3即為今日所提的條件機率的乘法原理 \(P(E\cap F)=P(E)P(F|E)\)，命題5則是貝氏定理，在 \(F\) 發生的情形下，計算 \(P(E|F) = \frac{{P(E \cap F)}}{{P(F)}}\)。

事實上，我們若將 \(F\) 視為「\(n\) 次試驗中事件發生的次數為 \(X\) 次」的事件，\(E\) 視為「\(r_1<x<r_2\)」的事件。貝葉斯的問題便是計算 \(P(E|F)\)。因此，只要能求出 \(P(F)\) 和 \(P(E\cap F)\) 即可。接著貝葉斯用了一個頗為獨特的想法，據以建立機率模型進行計算。而他使用的方法，請見〈貝葉斯和貝氏定理(3)〉。

連結：貝葉斯和貝氏定理(3)

參考文獻：

• Katz, V. J. (1993), A History of Mathematics, New York: HarperCollins College Publishers.
• Biography of Thomas Bayes, http://www-history.mcs.st-and.ac.uk/Biographies/Bayes.html
• An Essay towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, F. R. S. Communicated by Mr. Price, in a Letter to John Canton, A. M. F. R. S. https://archive.org/stream/philtrans09948070/09948070#page/n0/mode/2up
• 陳昱成，〈貝氏定理的應用〉，《科學教育月刊》第357期(2013)，頁19-28。

貝葉斯和貝氏定理(1)（Thomas Bayes and Bayes’ Theorem (1)）
臺北市立第一女子高級中學蘇俊鴻老師

貝氏定理(Bayes’ Theorem)在高中數學的機率單元中出現，被當成是條件機率的重要議題，為人所知的是它的定理內容：

設 \(\left\{ {{A_1},{A_2}, \cdots ,{A_n}} \right\}\) 為樣本空間 \(S\) 的一組分割，\(B\) 為 \(S\) 的任一個事件，
若 \(P(B)>0\)，則在事件 \(B\) 發生的情況下，事件 \(A_k\) 發生的機率為

\(\displaystyle P\left( {{A_k}|B} \right) = \frac{{P\left( {{A_k}} \right)P\left( {B\left| {{A_k}} \right.} \right)}}{{\sum\limits_{i = 1}^n {P\left( {{A_i}} \right)P\left( {B\left| {{A_i}} \right.} \right)} }},1\le k\le n\)

以及課本提及的應用，如品管檢驗、醫學檢定等。但多數人不知道貝氏是誰？什麼問題促使他發展出貝氏定理？貝氏定理在現今統計學上有著廣泛的應用，但學說提出之初，就如此為數學家和統計學家所擁護嗎？這些問題都是本文撰寫的動機。首先，就由托馬斯．貝葉斯(Thomas Bayes, 1702-1761)的生平開始說起，貝氏定理正是由他所提出的。 Continue reading →

數學之旅：三角形面積公式(II)
(Mathematical Journey through the Formulas of Triangle Area)
國立蘭陽女中陳敏晧教師

連結：數學之旅：三角形面積公式(I) 

4. 海龍公式：
   若 \(\Delta ABC\) 的三邊長 \(\overline {BC}= a,\overline {CA}= b,\overline {AB}= c\)，
   令 \(s = \frac{{a + b + c}}{2}\)，即三角形的半周長(semiperimeter)，
   則 \(a\Delta ABC = \sqrt {s(s – a)(s – b)(s – c)}\)，此稱為海龍公式(Heron’s formula)。證明：
   一般高中數學教科書常用代數方法證明，即利用餘弦定理及兩次平方差公式，如下敘述。
   (強調一下這並不是海龍當時的證明)
   \(\begin{array}{ll}a\Delta ABC&= \frac{1}{2}bc\sin A = \frac{1}{2}\sqrt {{b^2}{c^2}{{\sin }^2}A}\\&=\frac{1}{2}\sqrt {{b^2}{c^2}(1 – {{\cos }^2}A)}\\&=\frac{1}{2}\sqrt {{b^2}{c^2} – {b^2}{c^2}{{\left( {\frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}} \right)}^2}}\\&=\frac{1}{2} \cdot \frac{1}{2}\sqrt {{{\left( {2bc} \right)}^2} – {{\left( {{b^2} + {c^2} – {a^2}} \right)}^2}}\\&= \frac{1}{4}\sqrt {\left[ {\left( {{b^2} + 2bc + {c^2}} \right) – {a^2}} \right]\left[ {{a^2} – \left( {{b^2} – 2bc + {c^2}} \right)} \right]}\\&=\frac{1}{4}\sqrt {\left[ {{{\left( {b + c} \right)}^2} – {a^2}} \right]\left[ {{a^2} – {{\left( {b – c} \right)}^2}} \right]}\\&=\frac{1}{4}\sqrt {\left( {a + b + c} \right)\left( {b + c – a} \right)(a + b – c)\left( {a + c – b} \right)}\\&=\frac{1}{4}\sqrt {2s\left( {2s – 2a} \right)\left( {2s – 2b} \right)\left( {2s – 2c} \right)}\\&=\sqrt {s\left( {s – a} \right)\left( {s – b} \right)(s – c)}\end{array}\)
   在一般數學教學現場中，學生對於海龍公式證明的反應，通常是認為繁瑣、難以心神領會；可是對於這個公式的方便又折服不已，因為只要給定三邊長就可以算出三角形面積，這是多麼美麗的公式(beautiful formula)啊！不過值得提醒的是，學生常會將海龍公式寫成 \(a\Delta ABC = \frac{1}{2}\sqrt {s(s – a)(s – b)(s – c)}\)，箇中道理當然是受「三角形面積等於底邊長乘於對應高的一半」的影響。海龍公式除了是計算題的妙計外，有時針對特殊的證明，往往具有畫龍點睛的效果。例如：證明當三角形的周長固定時，正三角形的面積最大。
   證明：
   因為周長固定，所以，\(s\) 為定值。
   利用算幾不等式 \(\frac{{(s – a) + (s – b) + (s – c)}}{3} \ge \sqrt[3]{{(s – a)(s – b)(s – c)}}\)，
   等號成立時，\(s – a = s – b = s – c\)，即 \(a=b=c\)，
   所以 \({\left( {\frac{s}{3}} \right)^3} \ge (s – a)(s – b)(s – c)\)，而 \(s = \frac{{a + b + c}}{2} = \frac{{3a}}{2}\)，
   得 \((s – a)(s – b)(s – c) \le {\left( {\frac{a}{2}} \right)^3}\)，
   代入海龍公式 \(a\Delta ABC = \sqrt {s(s – a)(s – b)(s – c)}\le\sqrt {\frac{{3a}}{2}\cdot\frac{{{a^3}}}{8}}=\frac{{\sqrt 3 }}{4}{a^2}\)
   (此即為正三角形邊長為時的面積)。

   卡當諾(Girolamo Cardano, 1501-1576)所著的《偉大的技藝(Ars Magna，英譯為The Great art)》書中有一題有趣的三角形面積問題：(我就直譯為中文了)
   
   某三角形的第一邊比第二邊長 \(1\)，而第二邊又比第三邊長 \(1\)。若三角形的面積為 \(3\)，試求其三邊長。

   解法：
   假設三角形的三邊長為 \(x-1,x,x+1\)，
   根據海龍公式 \(a\Delta ABC = \sqrt {s(s – a)(s – b)(s – c)}\)，
   因為  \(s = \frac{{(x – 1) + x + (x + 1)}}{2} = \frac{{3x}}{2}\)，代入得 \(3 = \sqrt {\frac{{3x}}{2} \cdot \frac{{x + 2}}{2} \cdot \frac{x}{2} \cdot \frac{{x – 2}}{2}}\)，
   左右平方得 \(9 = \frac{{3{x^2}}}{{16}}\left( {{x^2} – 4} \right)\)，化簡得 \({\left( {{x^2}} \right)^2} – 4({x^2}) – 48 = 0\)，
   配方得 \({\left( {{x^2} – 2} \right)^2} = 52\)，即 \({x^2} = 2\sqrt {13}+ 2\)，所以 \(x = \sqrt {2\sqrt {13}+ 2}\)，
   因此，三邊長 \(\sqrt{2\sqrt{13}+2}- 1,\sqrt {2\sqrt{13}+2} ,\sqrt{2\sqrt{13}+2}+1\)。

5. 三斜求積術：秦九韶(1208-1261)是南宋時的數學家，著有《數書九章》，此書有三大特色：大衍求一術、秦九韶演算法、三斜求積術。
   
   《數書九章》卷五題二云：「以小斜冪并大斜冪，減中斜冪，餘半之，同乘於上。以小斜冪并大斜冪，減上，餘四約之為實，開平方，得積。」
   以白話文闡述，若三角形的三斜邊以小、中、大稱之，
   則 ​\( 三角形面積=\sqrt{\frac{1}{4}\big[小^2\cdot大^2-\big(\frac{大^2+小^2-中^2}{2}\big)^2\big]} \)​ 。

   已知：若三角形的三斜邊小、中、大，分別以 \(a,b,c\) 表示。
   求證：\(a\Delta ABC = \sqrt {\frac{1}{4}\left[ {{a^2} \cdot {c^2} – {{\left( {\frac{{{c^2} + {a^2} – {b^2}}}{2}} \right)}^2}} \right]}\)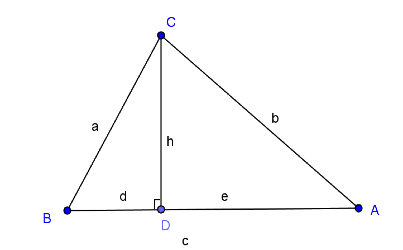
   證明：
   因為 \(\left\{ \begin{array}{l} c = d + e………\left( 1 \right)\\ {a^2} = {h^2} + {d^2}……\left( 2 \right)\\ b{}^2 = {h^2} + {e^2}……(3) \end{array} \right.\)，
   由 \((2)-(3)\) 得：\({a^2} – {b^2} = {d^2} – {e^2}\)，
   利用平方差得 \({a^2} – {b^2} = (d – e)(d + e) = c \cdot (d – e)\)，
   所以，\(d – e = \frac{{{a^2} – {b^2}}}{c}……(4)\)，
   由 \((1)+(4)\) 得：\(2d = c + \frac{{{a^2} – {b^2}}}{c} = \frac{{{c^2} + {a^2} – {b^2}}}{c}\)，因此，\(cd = \frac{{{c^2} + {a^2} – {b^2}}}{2}\)。
   \(\begin{array}{ll}a\Delta ABC &= \frac{1}{2}ch = \sqrt {\frac{1}{4}{c^2}{h^2}}\\&= \sqrt {\frac{1}{4}{c^2}({a^2} – {d^2})}\\&=\sqrt {\frac{1}{4}({a^2}{c^2} – {{(cd)}^2})}\\&=\sqrt {\frac{1}{4}\left[ {{a^2}{c^2} – {{\left( {\frac{{{c^2} + {a^2} – {b^2}}}{2}} \right)}^2}} \right]}\end{array}\)

   例如：三角形三邊長為 \(3,4,5\)，求三角形面積             __。
   解法：
   (1) 因為 \(3^2+4^2=5^2\)，得直角三角形，因此，面積為 \(\frac{1}{2}\times 3\times 4=6\)。
   (2) 利用海龍公式，令 \(a = 3,b = 4,c = 5,s = \frac{{a + b + c}}{2} = 6\)，
   則 \(a\Delta ABC = \sqrt {s(s – a)(s – b)(s – c)}= \sqrt {6 \times 3 \times 2 \times 1}= 6\)。
   (3) 利用三斜求積術，令 \(a = 3,b = 4,c = 5\)，
   則 \(\begin{array}{ll}a\Delta ABC &= \sqrt {\frac{1}{4}\left[ {{a^2} \cdot {c^2} – {{\left( {\frac{{{c^2} + {a^2} – {b^2}}}{2}} \right)}^2}} \right]}\\&=\sqrt {\frac{1}{4}\left[ {{3^2} \times {5^2} – {{(\frac{{{5^2} + {3^2} – {4^2}}}{2})}^2}} \right]}\\&=\sqrt {\frac{1}{4}(9 \times 25 – 9 \times 9)}\\&=\sqrt {\frac{1}{4} \times 9 \times 16}= 6\end{array}\)

總之，海龍公式與三斜求積術雖然形式看起來相異，但是，其本質是相同的，也可以說是等價的數學證明，有興趣的讀者何妨試試看！

連結：數學之旅：三角形面積公式(III)

數學之旅：三角形面積公式(I)
(Mathematical Journey through the Formulas of Triangle Area)
國立蘭陽女中陳敏晧教師

三角形面積公式是數學中面最常用的公式，也是大家在小學學數學的甜蜜記憶。

希臘哲人柏拉圖曾說：「畫在沙地上的三角形可以被抹去，但是，三角形的觀念不會受時間與空間的限制而留存下來。」可見三角形的觀念與發展會隨著人類數學發展而不斷變化。但是，不論如何演變，數學的新論點卻永遠根植於舊有的基礎上。

從個人學習數學的歷程看來，三角形的面積公式就如同是典範(paradigm)般的重要。我們可以透過公式的演變來重新釐清學習的轉移(shift)；當吾人從數學史的知識論脈絡切入，會發現三角形的面積公式從幾何學出發，邁向三角學領域，接引向量，拓展行列式，認識內積與外積，於解析幾何處發揚光大。 Continue reading →