算幾不等式的證明(II)(Inequality of arithmetic and geometric means)
國立蘭陽女中數學科陳敏晧老師

連結：算幾不等式的證明(I)

已知：\(a_1,a_2,…,a_n\) 為正數或零。

求證：

\(\displaystyle\frac{{{a_1} + {a_2} + … + {a_n}}}{n} \ge \sqrt[n]{{{a_1}{a_2}…{a_n}}}\)，“\(=\)” 成立時若且唯若，\(a_1=a_2=…=a_n\)。

(其中 \(\displaystyle\frac{{{a_1} + {a_2} + … + {a_n}}}{n}\) 稱為算術平均數，\(\sqrt[n]{{{a_1}{a_2}…{a_n}}}\) 稱為幾何平均數)。

除了常見的倒回的證明外(先證 \(n=2=2^1\) 再推論 \(n=4=2^2\)，然後反推 \(n=3\)，接著證明 \(n=8=2^3\)，然後反推 \(n=5,6,7\) 等)，在此處筆者再介紹兩種直接證明方法。

Continue reading →

算幾不等式的證明(I)(Inequality of arithmetic and geometric means)
國立蘭陽女中數學科陳敏晧老師

若 \(a,b\) 為正數或零，則 \(\displaystyle\frac{{a + b}}{2} \ge \sqrt {ab}\)，“\(=\)” 成立時若且唯若，\(a=b\)。

(其中 \(\displaystyle\frac{{a + b}}{2}\) 稱為 \(a,b\) 的算術平均數，\(\sqrt{ab}\) 稱為 \(a,b\) 的幾何平均數)

代數證明：

\(\displaystyle\frac{{a + b}}{2}-\sqrt {ab}= \frac{1}{2}(a + b – 2\sqrt {ab} ) = \frac{1}{2}{\left({\sqrt a-\sqrt b } \right)^2}\ge 0\)，

因此，\(\displaystyle\frac{{a + b}}{2} \ge \sqrt {ab}\)，“\(=\)” 成立時，\(\displaystyle\frac{1}{2}{(\sqrt a-\sqrt b)^2} = 0\)，

所以，\(a=b\)，反之亦然。

算幾不等式可以推廣至 \(n\) 的情形，也就是若 \(a_1,a_2,…,a_n\) 為正數或零，

則 \(\displaystyle\frac{{{a_1} + {a_2} + … + {a_n}}}{n} \ge \sqrt[n]{{{a_1}{a_2}…{a_n}}}\)，“\(=\)” 成立時若且唯若，\(a_1=a_2=…=a_n\)。

(其中 \(\displaystyle\frac{{{a_1} + {a_2} + … + {a_n}}}{n}\) 稱為 \(a_1,a_2,…,a_n\) 的算術平均數，\(\sqrt[n]{{{a_1}{a_2}…{a_n}}}\) 稱為 \(a_1,a_2,…,a_n\) 的幾何平均數) Continue reading →

賭金分配問題 (The Problem of Division of the Stakes)(二)
國立屏東高級中學數學科楊瓊茹老師

參考 賭金分配問題(一)

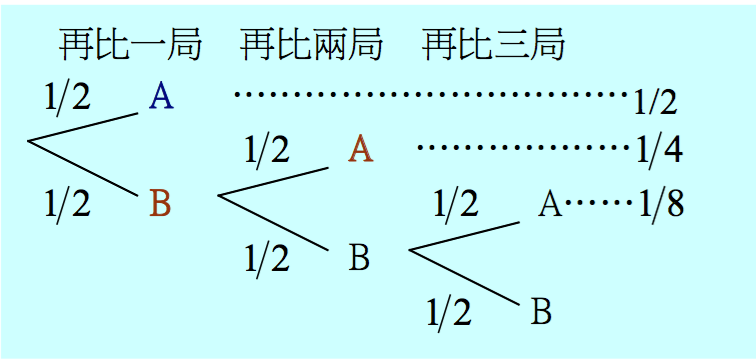
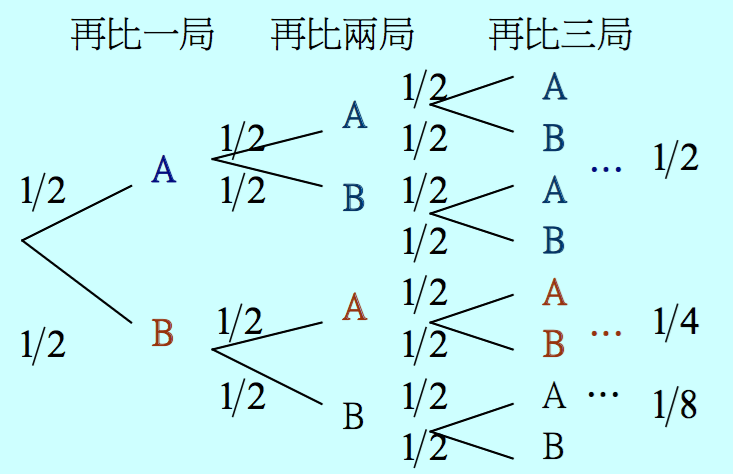
在費馬的解法中，他考慮再比賽三局所有可能的情況為(\(A\)表甲勝、\(B\)表乙勝)：

不過，還要比 \(3\) 局的計算方式似乎有些奇怪，因為在甲已勝 \(5\) 局的優勢下，AAA這三場中根本就不必再比最後兩局、BAB中也不用比最後一局。事實上，我們在甲得 \(6\) 勝時比賽就結束，這兩個想法乍看之下顯然有些不同，但其實是相同的。因為不管甲 \(6\) 勝時是否還打了後面那幾局，那些結果“依然存在”(參見樹狀圖)。

Continue reading →

賭金分配問題 (The Problem of Division of the Stakes)(一)
國立屏東高級中學數學科楊瓊茹老師

機率史上，賭金分配問題曾引起許多數學家們的討論，筆者將這些內容和數據略作調整，使得能夠用一道題目為例，分別呈現出數學家–帕西歐里、塔爾塔利亞、費馬和巴斯卡–對於賭金分配的看法：

假設甲乙兩人進行一場公平的比賽，且甲乙兩人實力相當，各出資 \(12\) 枚金幣作為賭注，必須要贏 \(6\) 局才能贏得賭金，目前甲以 \(5:3\) 領先。在此假設下，若比賽因故終止，則此時應如何分配賭金？

帕西歐里 ( Luca Pacioli, 1445-1509 ) 的解法根據已贏得的局數比例作分配，甲得 \({\rm{24}} \times \frac{{\rm{5}}}{{\rm{8}}} = {\rm{15}}\) 枚金幣、乙得 \({\rm{24}} \times \frac{{\rm{3}}}{{\rm{8}}} = {\rm{9}}\) 枚金幣。

塔爾塔利亞 ( Niccolò Tartaglia, 1499-1557 ) 注意到帕西歐里的答案是錯誤的，因為若假設局數比為 \(1:0\)，則甲拿走所有的賭金，這顯然毫無道理。他認為甲乙兩人相差 \(2\) 局，這 \(2\) 局的差距是總局數 \(6\) 局的三分之一，甲應拿走乙方賭金的三分之一，也就是甲得 \({\rm{12}} + \frac{{{\rm{(5 – 3)}}}}{{\rm{6}}} \times {\rm{12}} = {\rm{16}}\) 枚金幣，乙得 \({\rm{12 – }}\frac{{{\rm{(5 – 3)}}}}{{\rm{6}}} = {\rm{8}}\) 枚金幣。 Continue reading →

蒙提霍爾問題（Monty Hall problem）(二) 請問瑪麗蓮
國立屏東高級中學數學科楊瓊茹老師

連結：蒙提霍爾問題（一）決勝21點

回顧 1990 年 9 月 9 日，瑪麗蓮‧沃斯‧薩萬特 (Marilyn vos Savant) 在《繽紛遊行》(Parade) 的「請問瑪麗蓮」專欄中，回答讀者提出的三門問題，沃斯‧薩萬特是金氏世界紀錄最高智商 \(228\) 的人，她認為選擇換的勝算比較大。為了說服讀者，她請大家想像有 \(1,000,000\) 扇門，她說：

你選擇 \(1\) 號門，而主持人知道門後有什麼，他總是避開有獎的那扇門，除了 \(777,777\) 號門外，把別的門都打開了。這時你會毫不猶豫地換到另一扇門，是吧?」

換句話說，如果你選擇 \(1\) 號門，只有 \(1/1,000,000\) 的機率猜中，而汽車在其他門後的機率是 \(999,999/1,000,000\)。當主持人打開 \(999,999\) 扇門中的 \(999,998\) 扇門，但絕對不會打開有汽車的那扇，現在拜主持人之賜，\(1\) 號門除外，只剩下的這扇門代表所有 \(999,999\) 扇門的價值，\(999,999/1,000,000\) 的機率全都集中到這一扇門。 Continue reading →

蒙提霍爾問題 (Monty Hall problem)（一） 決勝21點
國立屏東高級中學數學科楊瓊茹老師

在 2008 年上映的美國電影《決勝21點》中，劇中主角班 (Ben Campbell)在非線性代數的課堂上與授課教授米奇(Mickey Rosa) 有一段精彩的對話：

米奇：「假設你正參加一個遊戲節目，你有機會從三扇不同的門裡選一扇，其中一扇門後面有一輛新車，另外兩扇門後面各有一頭山羊？你要選擇哪一扇門？」

班：  「一號門。」

米奇：「好！這時節目主持人，順便一提，他知道門後的秘密，他去打開另一扇門，比方說他開了三號門，後面是一頭山羊。這時節目主持人說：「班，你想要堅持選擇一號門，還是換成二號門？」現在問題是–改變選擇(換另一扇門)是否對你有利?」

班：  「是的」

米奇：「記住！主持人知道那輛車在哪裡，你怎麼知道他不是在耍你？……」 Continue reading →

樣本空間( Sample space)
國立屏東高級中學數學科楊瓊茹老師

日常生活中常使用到「可能」這個字眼，面對種種事先無法預知結果的隨機現象，觀察並求出可能產生的結果，這樣的過程叫做「試驗」。例如：投擲一顆公正的骰子，觀察它出現的點數，就是一項試驗，這項試驗有六種可能出現的結果，這些結果所形成的集合 \(S={1,2,3,4,5,6}\)，叫做「樣本空間」。簡而言之，一項試驗中所有可能發生的結果所形成的集合稱為「樣本空間」。

然而，要將可能的結果 (outcome) 看成空間中的樣本點的時候，有些微妙之處。1754年法國數學家達朗貝爾 (d’Alembert) 提出一個機率問題：

把一枚均勻的硬幣連擲兩次，至少擲出一次正面的機率是多少？

Continue reading →

班佛定律 (Benford’s Law)
國立屏東高級中學數學科楊瓊茹老師

現行的高中教科書中，有個非常有意思的題目：

審計工作者會使用班佛法則來查帳，班佛法則是：「銀行存款的最高位數字是 $$a$$ 者的比例約為 $$\log(1+\frac{1}{a})$$」﹒根據班佛法則﹐銀行存款的最高位數字是 $$4,5,6$$ 或 $$7$$ 者的比例約有
$$(1)~20\%$$   $$(2)~30\%$$   $$(3)~40\%$$   $$(4)~50\%$$   $$(5)~60\%$$ .

這個題目由簡單的對數運算性質，如下列算式得到答案 $$(2)~30\%$$。

$$\log \left( {1 + \frac{1}{4}} \right) + \log \left( {1 + \frac{1}{5}} \right) + \log \left( {1 + \frac{1}{6}} \right) + \log \left( {1 + \frac{1}{7}} \right) \\= \log \left( {\frac{5}{4} \times \frac{6}{5} \times \frac{7}{6} \times \frac{8}{7}} \right)=\log 2\approx 0.301$$

「班佛定律」又稱為首位數字法則 ( First-Digit Law )。 Continue reading →