改變歷史進程的17個方程式
臺北市立第一女子高級中學蘇俊鴻老師編譯/國立臺灣大學物理系王名儒教授責任編輯

編譯來源：The 17 Equations That Changed The Course Of History

數學圍繞在我們四周，它在許多方面型塑(shaped)我們對這個世界的理解。

2013年，身為數學家，也是科普作者的伊恩．史都華(Ian Stewart)出版了《改變世界的17個方程式》(The 17 Equations that Changed the World)一書。近來，我們在Dr. Paul Coxon的Twitter (由數學輔導老師，也是部落客的Larry Phillips所註冊)上發現這個他摘錄書中方程式所成的簡便表格： Continue reading →

無限的觀念～0.9是否等於1？
臺北市立西松高中 蘇惠玉教師

一、前言

目前高中教材中，有兩個部分涉及「無限」。首先是數學I，在一開始介紹數系的時候，學生要學會將循環小數化成分數。

在此之前，學生從來沒有接觸過「無限」的概念，也沒學過無窮等比級數如何求和，因此教師通常都是這樣教的：例如要將 \(0.\overline{12}\) 化成分數，令 \(0.\overline{12}=x\)，因為

\(x=0.\overline{12}=0.121212…\)

\(100x=12.121212…\)

將兩式相減得 \(99x=12\)，因此 \(x=\frac{12}{99}\)

這樣計算推理邏輯有個前提必須是假設 \(0.\overline{12}=0.121212…\) 這個無限小數是收斂的，其收斂值存在才能假設它為 \(x\)，並且以 \(x\)去進行運算。

Continue reading →

由問題的起源看導數的定義II
臺北市立西松高中 蘇惠玉教師

連結：由問題的起源看導數的定義I

在前一篇文章中，我們已經看過費馬求極值的方法了，也就是當 \(e\) 是個很微小的量時（亦即趨近於 \(0\)），讓 \(\frac{f(a+e)-f(a)}{e}\) 這個值「盡可能的逼近」\(0\)。

接下來我們來看看牛頓求切線的方法。

牛頓求切線的方法

下面的方法出現在牛頓的《曲線求積術》，撰寫於 1693 年，並於 1704 年作為《光學》一書的附錄正式發表。牛頓以求切線的策略與方法，說明他的「流數方法（即求導數的方法）」，並舉函數為 \(y=x^n\) 為例，實際演練操作他的方法。 Continue reading →

由問題的起源看導數的定義I
臺北市立西松高中 蘇惠玉教師

前言

在高中的微積分教學脈絡中，一定先教授極限的觀念與函數的極限，然後在進入微分單元時，直接定義何謂導數，即多項式函數 \(f(x)\) 在點 \((a,f(a))\) 的導數為 \(f'(a)=\lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}\)，然後再說明導數的意義以及應用。

然而為何導數要這樣定義？我們在定義一個數學物件之前，通常是問題導向的，有需要，才有發明。那麼導數或是微積分來自於什麼需求？為何會導致這樣的定義形式？在這一系列的文章中，筆者試圖透過這一段數學史的發展，從問題的源頭說起，經由費馬求極值與牛頓求切線的方法，並利用問題來學習與思考，最後理解何以會以 \(f'(a)=\lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a}\) 這種形式來定義導數的必然性。

Continue reading →

橢圓的參數式
臺北市立西松高中 蘇惠玉教師

圓的參數式

在二上的三角單元教學中，我們曾經學習過利用三角函數將直角坐標系上的點坐標，轉換成極坐標。對每一個直角坐標系統上的點 \(P(x,y)\)，設它與原點的距離 \(\overline{OP}\) 為 \(r=\sqrt{x^2+y^2}\)，
以 \(x\) 軸的正方向為始邊，逆時針旋轉到 \(\overrightarrow{OP}\)（\(\overrightarrow{OP}\) 為終邊）的角度為 \(\theta\)，
因此 \(P\) 點的極坐標表示為 \(P[r,\theta]\)。

既然同一點的坐標有兩種表徵，那麼直角座標與極坐標之間又該如何轉換呢？此時由廣義角的三角函數值定義可知 \(\cos\theta=\frac{x}{r},\sin\theta=\frac{y}{r}\)，因此可得 \(x=r\cos\theta,y=r\sin\theta\)。
亦即直角座標系統中的 \(x\) 與 \(y\) 坐標，可利用三角函數轉換成以極坐標中的 \(r\) 與 \(\theta\) 來表示。 Continue reading →

最短路徑問題
臺北市立西松高中 蘇惠玉教師

在數學III的直線單元中有這樣的問題：在坐標平面上，給定兩點 \(A\) 與 \(B\)，以及一直線 \(L\)，想要在 \(L\) 上找一點 \(P\)，使得 \(\overline{PA}+\overline{PB}\) 有最小值。這個 \(P\) 點要怎麼找呢？我們先把 \(L\) 特殊化，從 \(x\) 軸上的點來考慮。

例題1
坐標平面上給定兩點 \(A(1,3),B(5,-1)\)。
在 \(x\) 軸上找一點 \(P\)，使得 \(\overline{PA}+\overline{PB}\) 有最小值，\(P\) 點坐標為何？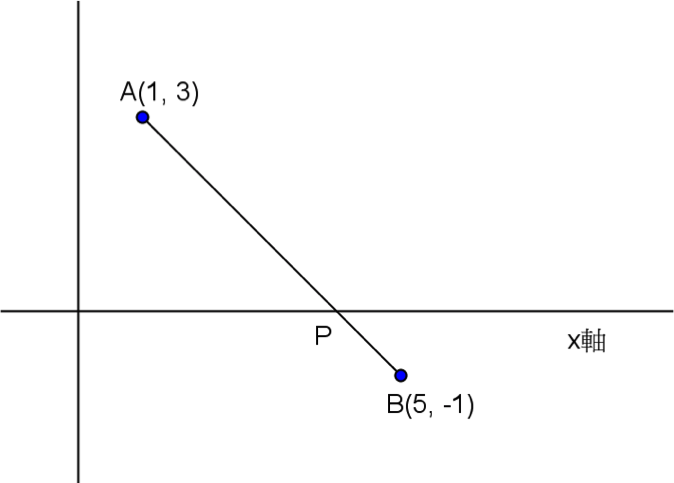

解：如圖，\(A,B\) 在 \(x\) 軸的異側。
由於兩點連線會與 \(x\) 軸相交，且兩點間直線距離最近，
因此當 \(P\) 點為 \(\overline{AB}\) 與 \(x\) 軸的交點時，此時 \(\overline{PA}+\overline{PB}\) 有最小值。
因為 \(\overleftrightarrow{AB}\) 的方程式為 \(x+y=4\)，故與 \(x\) 軸的交點為 \(P(4,0)\)，
此時所求最小值為 \(\overline{AB}=4\sqrt{2}\)。
由例題1可知，當 \(A,B\) 在所給直線 \(L\) 的異側時，
所要找的 \(P\) 點即為 \(\overleftrightarrow{AB}\) 與 \(L\) 的交點。
那麼當 \(A,B\) 都在 \(L\) 的同側時，要如何找到 \(P\) 點呢？

Continue reading →

座標平面上的旋轉變換
臺北市立西松高中 蘇惠玉教師

二階方陣所對應的旋轉變換

將平面上的點 \(P(x,y)\)，以坐標軸原點 \(O\) 為旋轉中心，逆時針旋轉 \(\theta\) 角（當 \(\theta<0\) 時可考慮為順時針旋轉），得到點 \(P\) 經旋轉之後的像為 \(P’=(x’,y’)\)，這樣的變換稱為旋轉變換。

我們先以極坐標來表示 \(P\) 點坐標：
在坐標平面上，若 \(P\) 點到原點 \(O\) 的距離為 \(r\)，以 \(x\) 軸正向為始邊，
逆時針旋轉到 \(\overrightarrow{OP}\) 的角度為 \(\alpha\)，那麼點 \(P(x,y)\) 的極坐標為 \(P[r,\alpha]\)，
且 \(x=r\cos \alpha,y=r\sin \alpha\)，
並可得點 \(P\) 經逆時針旋轉 \(\theta\) 角的像 \(P’=(x’,y’)\) 的極坐標為 \(P'[r,\alpha+\theta]\)，
其中 \(x’=r\cos {(\alpha+\theta)},y=r\sin {(\alpha+\theta)}\)。 Continue reading →

直式開方法開平方根
臺北市立西松高中 蘇惠玉教師

目前的高中數學教材中，已經不再教授開平方的直式開方法，在課綱中只要求學生會估計平方根的近似值即可。然而在統計部分的單元學習中，仍有些題目要求學生計算某些牽涉到平方根統計量的近似值，例如標準差。在筆者的教學經驗中，常有學生會問如何開平方根，因此筆者將在此篇文章中，以中國古算的開方術為基礎，介紹所謂的直式開方法。

《九章算術》〈少廣〉卷中有問：
今有積五萬五千二百二十五步。問為方幾何？
開方術曰：置積為實。借一筭，步之，超一等。議所得，以一乘所借一筭為法，而以除。除已，倍法為定法。其復除。折法而下。復置借筭，步之如初，以復議一乘之，所得副以加定法，以除。以所得副從定法。復除，折下如前。

這一段開方術，看起來不太好理解，由於古時候中算以算籌代筆，計算的過程實際上就是算籌的操弄，因此術文中有一些是算籌所帶來的難度，在此忽略不管。同時在劉徽的注釋中，他也提供了一個相當清楚簡潔的幾何解釋。 Continue reading →