條件機率(3)：一個問題的澄清（Conditional Probability (3)：Clarifying a problem）
臺北市立第一女子高級中學蘇俊鴻老師

連結：條件機率(2)：乘法定律

再次重述在〈條件機率(2)：乘法定律〉中所提出問題：

某人拜訪有兩個孩子的一對夫婦，當場已有一個男孩在座。假設生男生女的機會相等，求此夫婦兩小孩皆為男孩的機率？

或許幾經思考，這個問題總讓你聯想對應到〈條件機率(1)：定義〉中提及的某個典型的例題：

投擲公正硬幣兩次，已知擲出一次正面的情形下，求投擲兩次皆為正面的機率。

那麼，何以機率為 \(\frac{1}{3}\)，這個看來似乎正確答案值得商榷？這正是本文的目的，透過這個問題的討論，希望能夠建立起將機率應用在實際生活問題時，需要更加小心的印象。以下容我們加以說明原由。

Continue reading →

條件機率(2)：乘法定律（Conditional Probability (2)：Multiplication Law）
臺北市立第一女子高級中學蘇俊鴻老師

連結：條件機率(1)：定義

在回答〈條件機率(1)：定義〉最後留下的問題前，

我們再來看條件機率的定義：\(P\left( {B|A} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}}\)，\(P(A)>0\)。

將式子整理可得 \(P\left( {A \cap B} \right) = P\left( A \right) \cdot P\left( {B|A} \right)\)

這個式子說明著：事件 \(A\) 和 \(B\) 兩事件同時發生的機率，會等於事件 \(A\) 發生的機率乘上在 \(A\) 發生的條件下事件 \(B\) 發生的機率。它不僅揭示了討論條件機率的必要性，也告訴我們數個事件同時發生的機率，該如何依次處理。進一步，我們能推論下列式子都是成立的：

(1)   若 \(P(B)>0\)，\(P\left( {A \cap B} \right) = P\left( B \right) \cdot P\left( {A|B} \right)\)

(2)   若 \(P(A \cap B) > 0\)，\(P\left( {A \cap B \cap C} \right) = P\left( A \right) \cdot P\left( {B|A} \right) \cdot P\left( {C|A \cap B} \right)\)  Continue reading →

條件機率(1)：定義（Conditional Probability (1)：Definition）
臺北市立第一女子高級中學蘇俊鴻老師

條件機率(Conditional Probability)，如同字面意義，是在假設某事件發生的條件下，考慮原本事件發生的機率。例如，投擲公正硬幣兩次，出現兩次正面的機率為 \(\frac{1}{4}\)。若我們加上「已知第一次擲出正面」的條件的話，那麼出現兩正面的機率將變成 \(\frac{1}{2}\)。事實上，若是掌握條件機率的定義，倒也不難理解箇中變化：

設 \(A,B\) 為兩事件且 \(P(A)>0\)。
在事件 \(A\) 發生的情況下，事件 \(B\) 發生的機率的條件機率，以 \(P(B|A)\) 表示，
且定義 \(\frac{P(A\cap B)}{P(A)}\)。

Continue reading →

從複數到三角函數公式(II) (From complex number to trigonometric function formulas)
國立蘭陽女中陳敏晧教師

連結：從複數到三角函數公式(I) 

證明：

(1) \(\displaystyle\sin \theta+ \sin 2\theta+\cdots+ \sin n\theta= \frac{{\sin \frac{{(n + 1)\theta }}{2} \cdot \sin \frac{{n\theta }}{2}}}{{\sin \frac{\theta }{2}}}\)

(2) \(\displaystyle\cos \theta+\cos 2\theta+\cdots+ \cos n\theta= \frac{{\sin \frac{{n\theta }}{2}\cos \frac{{(n + 1)\theta }}{2}}}{{\sin \frac{\theta }{2}}}\)

第二種證明方法：利用複數的概念。

我們可以使用歐拉公式 \({e^{i\theta }}= \cos \theta+ i\sin \theta\)，

若將 \(\theta\) 以 \(-\theta\) 代入可得 \({e^{ – i\theta }}= \cos \theta- i\sin \theta\)，

可得 \(\left\{ \begin{array}{l}\displaystyle \cos \theta= \frac{{{e^{i\theta }}+ {e^{ – i\theta }}}}{2}\\\displaystyle\sin \theta = \frac{{{e^{i\theta }}-{e^{ – i\theta }}}}{{2i}} \end{array} \right.\)，變換變數得 \(\left\{ \begin{array}{l}\displaystyle\cos \frac{\theta }{2} = \frac{{{e^{\frac{{i\theta }}{2}}} + {e^{\frac{{ – i\theta }}{2}}}}}{2}\\\displaystyle\sin \frac{\theta }{2} = \frac{{{e^{\frac{{i\theta }}{2}}} – {e^{\frac{{ – i\theta }}{2}}}}}{{2i}} \end{array} \right.\)

Continue reading →

從複數到三角函數公式(I) (From complex number to trigonometric function formulas)
國立蘭陽女中陳敏晧教師

複數在數學各領域均有重大影響，本文章將討論如何以複數的形式來證明三角函數的相關公式，由於複數具有極坐標形式，可以將角度做旋轉、長度做伸縮變換，這是傳統幾何學在直角坐標平面難以突破的面向，因此，利用複數來證明三角函數公式往往會有意想不到的收穫，也常使學習者見識到數學之美！

本文將使用到歷史法國數學家棣美弗(Abraham de Moivre, 1667-1754)於1730年發表的棣莫弗公式，即若 \(z = r(\cos \theta+ i\sin \theta)\)，則 \({z^n} = {r^n}(\cos n\theta+ i\sin n\theta ),n \in Z\)。

及歐拉(Leonhard Euler, 1707-1783)在1748年所發表的歐拉公式：\({e^{i\theta }} = \cos \theta+ i\sin \theta\)。

Continue reading →

和算家求橢圓周長的方法（二）
（Wasan’s method of finding the formula of the circumference of an ellipse Ⅱ）
臺北市立和平高中教師黃俊瑋

連結：和算家求橢圓周長的方法（一）

如前文〈和算家求橢圓周長的方法（一）〉所述，和田寧是最早造出正確橢圓周長展開式的數學家，然而，他的主要著作皆在西元1836年的一場大火中付之一炬，因此，我們只得以他授予的弟子們的傳書，一窺他求解橢圓周長的方法。

和田寧的弟子小出兼政，依據和田寧所授之傳書編成《圓理算經》，該書〈上卷〉的第五部份裡，提出了求橢圓周長問題：「譬今有如圖橢圓，只言長徑若干，短徑若干，問得周長術如何？」作者造橢圓周長公式的過程中，主要是利用分割求和的積分方式，輔以各類「圓理表」。以下，筆者進一步說明並分析他求橢圓周長的過程。

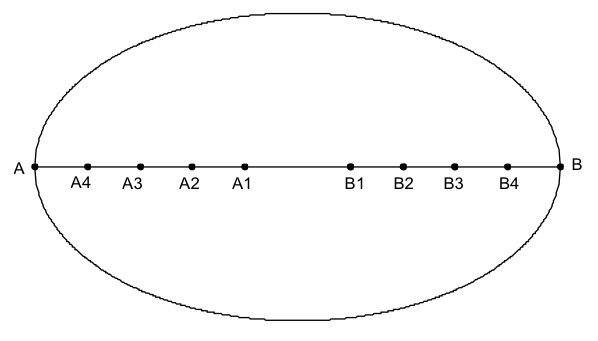
假設橢圓之長軸長為 \(2a\)、短軸長為 \(2b\)，首先，小出兼政先利用「截弦順法對橢圓之長軸作分割，配對得到 \(n\) 段，讀者請參考圖一，以分割成配對 \(5\) 等分的情況為例作說明。此分割法是以左右配對 \(5\) 等分割的方式，對橢圓之長軸作分割，使其滿足：

 \(\overline{{A_1}{B_1}}=\overline {{A_1}{A_2}}+\overline {{B_1}{B_2}}=\overline{{A_2}{A_3}}+\overline{{B_2}{B_3}}= \overline{{A_3}{A_4}}+\overline{{B_3}{B_4}}=\overline{{A_4}A}+\overline{{B_4}B}=\frac{{2a}}{5}\)

這和現代教科書中所用的等分割方式有所不同。

Continue reading →

和算家求橢圓周長的方法（一）
（Wasan’s method of finding the formula of the circumference of an ellipse Ⅰ）
臺北市立和平高中教師黃俊瑋

相較於圓周長與而言，橢圓周長是早期數學家們感到棘手的問題。一般而言，我們可以利用定積分法，求得橢圓的面積。

首先，不失一般性，我們可把橢圓的長軸固定在 \(x\) 軸的方向上，
則其標準方程式為：\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) （長軸半長為 \(a\)，短軸半長為 \(b\)）。
當我們考慮函數 \(y=\sqrt{b^2-\frac{b^2}{a^2}x^2}=\frac{b}{a}\sqrt{a^2-x^2}\) 時，可以利用定積分求得橢圓面積為第一象限部份面積的 \(4\) 倍（如圖一所示），即 \(ab\pi\)。特別地，當橢圓的長軸與短軸等長（亦即當 \(2a=2b\)）時，可得圓面積公式 \(\pi a^2\)。

Continue reading →

平面上點到直線距離（三） (The distance from a point to a line in the plane Ⅲ）
臺北市立和平高中教師黃俊瑋

連結：平面上點到直線距離（二）

本文承〈平面上點到直線距離(一)〉與〈平面上點到直線距離(二)，繼續提出三類平面上點到直線距離的解法以及相關討論與連結。而本文中的各類解法，主要在直線上任取一點或兩點，造出新向量，所延伸出的方法。

方法5：在直線上任取一點，再利用平行與垂直性質

本類方法主要是引入直線上的一點後，充份利用直線的法向量與方向向量，輔以平行與垂直相關性質與關係，求得投影點與距離。

方法5-1：在直線上任取一點，再利用平行與垂直相關性質

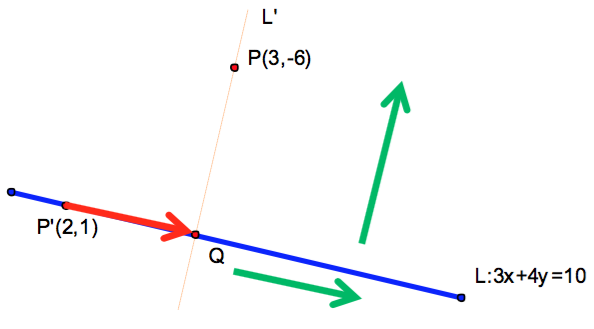
在 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\)，則 \(\vec{P’P}=(1,-7)\) ，
令 \(Q\) 為 \(P(3,-6)\) 在 \(L\) 的投影點，\(\vec{P’Q}\) 與直線之方向向量平行，可設為 \(\vec{P’Q}=t(4,-3)\)。

接下來，可發展出兩種方法，分別利用直線的法向量或方向向量，搭配平行與垂直關係進行解題：

5-1-1

則 \(\vec{QP}=\vec{P’P}-\vec{P’Q}=(1-4t,-7+3t)\) 平行直線 \(L:3x+4y=10\) 的法向量
分量成比例 \(\frac{{1 – 4t}}{{ – 7 + 3t}} = \frac{3}{4}\)，可得 \(4(1-4t)=3(-7+3t)\)，解之可得 \(t = 1\)，
可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求。

5-1-2

\(\vec{QP}=\vec{P’P}-\vec{P’Q}=(1-4t,-7+3t)\) 垂直直線 \(L:3x+4y=10\) 的方向向量
內積為 \(4(1 – 4t) + ( – 3)( – 7 + 3t) = 0\)，解之可得 \(t = 1\)，
可得投影點為 \(Q(6,-2)\)，則 \(\overline{PQ}\) 之距離 \(5\) 即為所求(參考圖一所示)。

Continue reading →