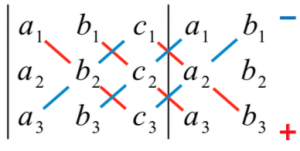- 行列式的應用 2014/09/17
行列式的應用（Applications of Determinant）
國立臺南第一高級中學林倉億老師連結：行列式的性質
以下介紹行列式在高中數學中主要的應用：
- 表示平面上三角形的面積
\(\vec{OA}=(a_1,b_1)\)、\(\vec{OB}=(a_2,b_2)\)，則 \(\Delta OAB\) 面積 \(= \frac{1}{2}\left| {\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|} \right|\)
（\(\frac{1}{2}\) 乘以 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|\) 的絕對值）。
【證明】：
由三角形面積公式 \(\Delta OAB = \frac{1}{2}\sqrt {{{\left| {\vec{OA}} \right|}^2}{{\left| {\vec{OB}} \right|}^2} – {{\left( {\vec{OA} \cdot\vec{OB}} \right)}^2}}\)
可得
\(\begin{array}{ll}\Delta OAB &= \frac{1}{2}\sqrt {({a_{ 1}}^2 + {b_{ 1}}^2)({a_{ 2}}^2 + {b_{ 2}}^2) – {{\left( {{a_{ 1}}{a_{ 2}} + {b_{ 1}}{b_{ 2}}} \right)}^2}} \\&= \frac{1}{2}\sqrt {{a_{ 1}}^2{b_{ 2}}^2 + {a_{ 2}}^2{b_{ 1}}^2 – 2{a_{ 1}}{a_{ 2}}{b_{ 1}}{b_{ 2}}} = \frac{1}{2}\sqrt {{{\left( {{a_{ 1}}{b_{ 2}} – {a_{ 2}}{b_{ 1}}} \right)}^2}} \\&= \frac{1}{2}\sqrt { {{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}^2}} = \frac{1}{2}\left| {\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|} \right|\end{array}\) - 表示空間中兩不平行向量的外積
\(\vec{OA}=(a_1,b_1,c_1)\)，\(\vec{OB}=(a_2,b_2,c_2)\)，則 \(\vec{OA}\) 與 \(\vec{OB}\) 的外積
可記作 \(\vec{OA}\times\vec{OB}= ( \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 2}}}&{{c_{ 2}}} \end{array} } \right| , \left| { \begin{array}{*{20}{c}} {{c_{ 1}}}&{{a_{ 1}}}\\ {{c_{ 2}}}&{{a_{ 2}}} \end{array} } \right| , \left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| )\) Continue reading → - 行列式的性質 2014/09/16
行列式的性質（Properties of Determinant）
國立臺南第一高級中學林倉億老師連結：行列式的定義
在本文中，二階行列式的定義是 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| = {a_{ 1}}{b_{ 2}} – {a_{ 2}}{b_{ 1}}\)，
三階行列式的定義則是
\(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}}&{{c_{ 2}}}\\ {{a_{ 3}}}&{{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| = {a_{ 1}} \cdot \left| { \begin{array}{*{20}{c}} {{b_{ 2}}}&{{c_{ 2}}}\\ {{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| – {a_{ 2}} \cdot \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| + {a_{ 3}} \cdot \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 2}}}&{{c_{ 2}}} \end{array} } \right| = {a_{ 1}}{b_{ 2}}{c_{ 3}} – {a_{ 1}}{b_{ 3}}{c_{ 2}} + {a_{ 2}}{b_{ 3}}{c_{ 1}} – {a_{ 2}}{b_{ 1}}{c_{ 3}} + {a_{ 3}}{b_{ 1}}{c_{ 2}} – {a_{ 3}}{b_{ 2}}{c_{ 1}}\)
我們稱直的為行，由左而右依序是第1行、第2行、…；稱橫的為列，由上而下依序是第1列、第2列、…。利用定義，很容易可以推出下列二階與三階行列式性質，證明就略去。 Continue reading →
- 行列式的定義 2014/09/16
行列式的定義 (Definitions of Determinant)
國立臺南第一高級中學林倉億老師在高中數學課本中，對於二階與三階行列式，基本上都是直接給出操作型定義：
定義1：\(\left| {\begin{array}{*{20}{c}} {{a_{1}}}&{{b_{1}}}\\ {{a_{2}}}&{{b_{2}}} \end{array}} \right| = {a_{1}}{b_{2}} – {a_{2}}{b_{1}}\)。
等號的左邊稱為二階行列式，等號的右邊稱為二階行列式的展開式，或稱為二階行列式的值。
定義2：\(\left| {\begin{array}{*{20}{c}} {{a_{1}}}&{{b_{1}}}&{{c_{1}}}\\ {{a_{2}}}&{{b_{2}}}&{{c_{2}}}\\ {{a_{3}}}&{{b_{3}}}&{{c_{3}}} \end{array}} \right| = {a_{1}}{b_{2}}{c_{3}} + {a_{2}}{b_{3}}{c_{1}} + {a_{3}}{b_{1}}{c_{2}} – {a_{3}}{b_{2}}{c_{1}} – {a_{2}}{b_{1}}{c_{3}} – {a_{1}}{b_{3}}{c_{2}}\)
等號的左邊稱為三階行列式，等號的右邊稱為三階行列式的展開式，或稱為三階行列式的值。
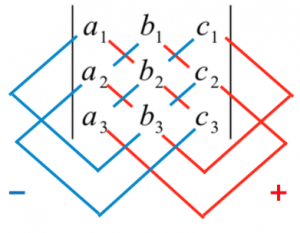
然後再根據定義推導相關的運算性質，最後再介紹它們的應用。定義二其實很難記憶，因此一般教科書都會補充記憶的方法，就是將圖一或圖二中，紅線上的數乘積之和，減去藍線上的數乘積之和。
圖一
圖二
- 等差數列 (Arithmetic Progression) 2014/09/15
等差數列 (Arithmetic Progression)
國立蘭陽女中陳敏晧教師一連串有次序的數，稱為數列(sequence)。其中的數，稱為項(term)；第一個項，稱為首項，以 \(a_1\) 表示；第 \(n\) 個項以 \(a_n\)表示。若數列中每一個後項減去前項的值固定時，則稱此數列為等差數列(Arithmetic Progression，簡寫為AP)，我們將此固定差值稱為公差(common difference)，以 \(d\) 表示。
因為 \(a_2-a_1=d\)，所以 \(a_2=a_1+d\)。又 \(a_3-a_2=d\)，所以 \(a_3=a_2+d=a_1+2d\)。我們很容易推得 \(a_n=a_1+(n-1)d,~n\in \mathbb{N}\)。進一步可得 \({a_n} = {a_m} + (n – m)d\)，其中 \(n,m\in \mathbb{N}\)。
- 另一個重要的無理數：e （Another important irrational number：e） 2014/09/15
另一個重要的無理數：e （Another important irrational number：e）
臺北市立和平高中教師黃俊瑋現今高中一年級課程中的〈數與式〉單元裡，簡單地討論了數系家族中的各個成員。其中，無理數最令一般人感到陌生、無法捉摸。教材中除了介紹諸如 \(\sqrt{n}\) 以及 \(a+\sqrt{b}\) 類的常見無理數外，也介紹了大家熟知的無理數－圓周率 \(\pi\)。
然而，我們也知道，實數線上密密麻麻地佈滿了無窮多個無理數。換句話說，浩瀚的實數世界裡，除了上述常見無理數之外，想必尚有其它忝為人知的成員。除了 \(\pi\) 之外，另一個著名的成員為自然對數的底數 \(e\)。至於 \(e\) 是什麼東東呢？以下我們說分明。
由於 \(e\) 總喜歡藏身自然與生活中，所以我們先來考慮一個與複利有關的問題：假設本金為 \(1\) 單位，並以複利的方式計算。
若利率為 \(100\%\)，那麼 \(1\) 年後本利和為 \((1+1)^1=2\)。
若改成半年支付一次利息，則利率減半為 \(\frac{1}{2}\cdot 100\%\)。
那麼，\(1\) 年後本利和為：\((1+\frac{1}{2})^2=\frac{9}{4}=2.25\)若改成四個月支付一次利息，則利率變為 \(\frac{1}{3}\cdot 100\%\)。
那麼，\(1\) 年後本利和為：\((1+\frac{1}{3})^3=\frac{64}{27}\approx 2.370…\)若改成三個月支付一次利息，則利率變為 \(\frac{1}{4}\cdot 100\%\)。
那麼，\(1\) 年後本利和為：\((1+\frac{1}{4})^4=\frac{625}{256}\approx 2.441…\)\(\cdots\)
以此類推，當利率變成原本的 \(\frac{1}{n}\)，支付次數變成 \(n\) 次，則 \(1\) 年後本利和為：\((1+\frac{1}{n})^n\)
如此，我們可或得一個數列〈\((1+\frac{1}{n})^n\)〉，其中 \(n\) 為自然數。 Continue reading →
- 集合的元素個數：無窮集合（三） The cardinality of a set: Infinite sets III 2014/09/12
集合的元素個數：無窮集合（三） The cardinality of a set: Infinite sets III
臺北市立和平高中教師黃俊瑋前文〈集合的元素個數：無窮集合（二）〉提到，實數的無窮為不可數無窮。那麼，在我們常見的數系或幾何例子裡，是否容易找到比實數更大的無窮呢？以幾何的觀點來看，實數對應於一維世界的直線，讀者可能會猜測，我們僅需將維度推廣，利用二維平面的實數數對，甚至三維空間的實數數對，想必可輕易造出更大的無窮。然而，事實並非如此！
首先，我們來討論下述問題：
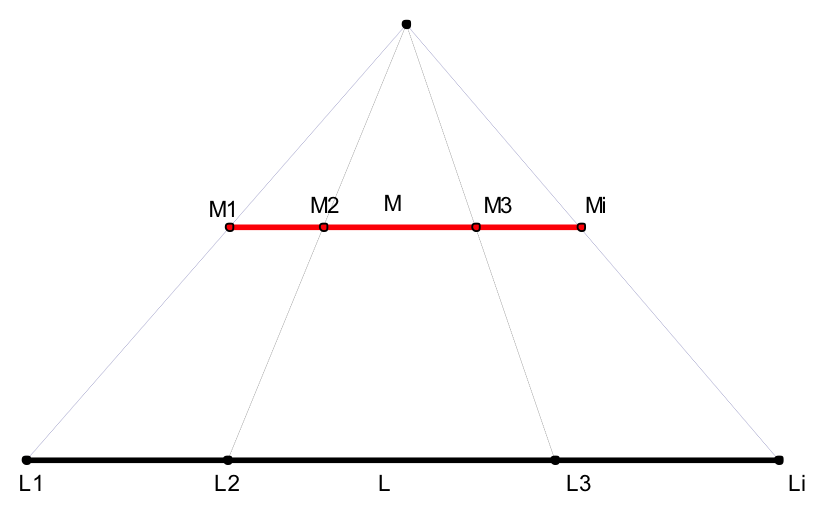
問題一：已知兩條不等長的線段 \(L\) 與 \(M\)，長度分別為 \(l\) 與 \(m\)，且 \(l>m\)，那麼，哪一條線段上的點較多呢？
直覺上，必定會認為是長度較長者點的數量較多。然而，如圖一所示，為兩不等長線段，從圖形可看出這兩條線段上的點，存在一一對應的關係。此對應圖對任意兩線段皆適用。
圖一 兩條不等長線段上的點之間，存在一一對應關係
- 集合的元素個數：無窮集合（二） The cardinality of a set: Infinite sets II 2014/09/12
集合的元素個數：無窮集合（二） The cardinality of a set: Infinite sets II
臺北市立和平高中教師黃俊瑋前文〈集合的元素個數：無窮集合（一）〉之中，我們討論了自然數、整數與有理數的個數，這些集合皆為可數集。而可數無限為基數最小的無限，我們一般將此基數命作 \({\aleph _0}\)（aleph與下標零，此符號可讀作阿列夫零）。
數學家康托爾提出了，構造出基數更大集合的方法：以一集合所有子集合為元素的新集合，其基數比原集合大。譬如說吧！令 \(S = \{ 1,2,3\}\)，則所構造出的新集合為：\(\{ \{ 1,2,3\} ,\{ 1,2,3\} ,\{ 1,2\} ,\{ 1,3\} ,\{ 2,3\} ,\{ 1\} ,\{ 2\} ,\{ 3\} ,\emptyset\}\)，它共包含了 \(8\) 個元素，而 \(8\)恰為 \(2^3\)。不難看出，原集合的元素個數為 \(n\)，則新集合的元素個數為 \(2^n\)。因此，我們可構造出一個基數為 \(2^{\aleph _0}\) 的新集合，如此可不斷地構造出更大的集合。
而我們把 \({\aleph _0}\)、\(2^{\aleph _0}\) 等涉及無窮集合的基數稱為超限基數（transfinite cardinal number）。那實數呢？問題似乎變難了，不像整數或有理數易於排序，我們很難有系統地將實數重新排序，使其與自然數一一對應，換言之，實數的個數問題，顯得更難以掌握。所以，我們不禁懷疑，實數的個數與自然數一樣多嗎？ Continue reading →
- 集合的元素個數：無窮集合（一） The cardinality of a set: Infinite sets I 2014/09/12
集合的元素個數：無窮集合（一） The cardinality of a set: Infinite sets I
臺北市立和平高中教師黃俊瑋無窮集合元素個數相等的定義如下：
若兩個集合（無窮集合）之間存在一一對應關係，則這兩個集合的元素個數相等。
我們可藉此發現許多違反直覺的例子。首先，就直觀上來看，正整數的個數比正偶數的個數來得多，而正整數的個數也比完全平方數來得多，不過，我們依上述定義實際作對應與比較後，會發現：
\(\begin{array}{lllllll} 1&2&3&4&5&\cdots&n\\\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&&\updownarrow\\2&4&6&8&10&\cdots&2n\end{array}\)
換言之，正整數的個數與正偶數的個數一樣多。類似地，我們也會發現：
\(\begin{array}{lllllll} 1&2&3&4&5&\cdots&n\\\updownarrow&\updownarrow&\updownarrow&\updownarrow&\updownarrow&&\updownarrow\\1^2&2^2&3^2&4^2&5^2&\cdots&n^2\end{array}\)
因此，正整數的個數與平方數的個數一樣多。這是不是既違反直覺又不可思議呢？ Continue reading →
- 行列式的定義 2014/09/16
- 表示平面上三角形的面積
