撲克牌遊戲與機率（二） (Poker game and the probability II)
臺北市立和平高中黃俊瑋教師

連結：撲克牌遊戲與機率（一） 

〈撲克牌遊戲與機率（一）〉一文中，介紹了撲克牌遊戲─梭哈─的前五種牌型之組合數與出現機率，接下來，本文繼續介紹如何求得其它四種牌型的組合數與機率。最後，表列出各類牌型對應的組合數與機率之實際計算結果，並作一簡單討論與說明。

6. 三條（three of a kind）

所謂的三條指的是 \(5\) 張牌當中，有三張數字相同，另兩張則都不相同。

例如：\(AAAKQ\)、\(99962\)、\(777Q8\) 等皆是，亦即其牌型為 \(aaabc\)。

我們可以利用下述方式計算出其組合數：先從 \(13\) 個數字中選出 \(1\)個作為 \(a\)，

再從其它 \(12\) 個數字中選出 \(2\) 個作為 \(b\) 與 \(c\)（這裡請注意，\(bc\)不需考慮順序，直接一次選取即可。否則若依序選完 \(a\)，再選 \(b\)，再選 \(c\) 會發生重複的情況，例如 \(AAAKQ\) 與 \(AAAQK\)）。

接著，從 \(4\) 種花色的數字 \(a\) 恰選三張：\(C_3^{4}\)，從 \(4\) 種花色的數字 \(b\) 恰選一張：\(C_1^{4}\)，

最後，從 \(4\) 種花色的數字 \(c\) 恰選一張：\(C_1^{4}\)。

如此，利用乘法原理可計算出所有的三條共有：\(C_1^{13}C_2^{12}C_3^{4}C_1^{4}C_1^{4}=54,912\) 種。

其出現的機率為：\(\displaystyle\frac{C_1^{13}C_2^{12}C_3^{4}C_1^{4}C_1^{4}}{C_5^{52}}\)。此值約為 \(0.02113\)。 Continue reading →

撲克牌遊戲與機率（一） (Poker game and the probability I)
臺北市立和平高中黃俊瑋教師

一副公正的撲克牌（Poker）共有四種花色（黑桃、紅心、方塊與梅花），各種花色包含\(13\)種數字（\(2\)、\(3\)、\(\cdots\)、\(10\)、\(J\)、\(Q\)、\(K\)、\(A\)）各一張，總共\(52\)張，有時會再加上\(2\)張鬼牌。而撲克牌相關遊戲種類相當多，其中，一種常見的遊戲方式是每人發五張牌，依據牌面花色與點數所形成的牌型來決定勝負（即一般人口中所謂的梭哈）。多年前，賭神、賭俠、賭聖系列等多部膾炙人口的電影，當中藉以比賽的撲克牌遊戲皆為此類。

遊戲當中，各類牌型的勝負比較如下：同花順 > 鐵隻 > 葫蘆 > 同花 > 順 > 三條 > 兩對 > 一對 > 其它（亂牌）。當然在同一牌型之下，必需依據相對應的數字大小來作比較。數字由大至小依序為：\(A>K>Q>J>10>9>\cdots>2\)；而在某些組合中 \(A\) 也可被視為 \(1\)。也由於各類牌型的機率計算上，僅需要古典機率與組合的概念即可，因此，無論是當年的聯考或者高中機率單元的補充教材裡，皆可看見此遊戲的蹤跡。

你也許會好奇，為什麼這些牌型大小需如此規定呢？問題的答案與機率有關。首先，從 \(52\) 張牌中取 \(5\) 張牌的所有可能性共有 \(C_5^{52}\) 種。以下，我們便對各類牌型的組合數與機率作一簡單討論與說明。在本文中，將先討論前五種牌型，而〈撲克牌遊戲與機率（二）〉中繼續討論另外四種牌型，並作進一步綜合討論。屆時讀者不難了解遊戲設計者如此規定的原因。 Continue reading →

我們同一天生日（二）！（We have the same birthday!）
臺北市立和平高中黃俊瑋教師

連結：我們同一天生日（一）！（We have the same birthday!）

〈我們同一天生日（一）〉一文中討論了下述問題：某一群人數共有 \(n\) 人，其中有某 \(2\) 個人同一天生日的機率為何？特別地，當這群人的人數到達 \(23\) 人以上時，有某 \(2\) 個人同一天生日的機率將大於 \(1/2\)。

該文中利用反面作法，先計算 \(n\) 個人生日皆不同天的機率為：

\(\frac{{365}}{{365}} \times \frac{{364}}{{365}} \times \frac{{363}}{{365}} \times\cdots\times \frac{{365 – n + 1}}{{365}}\)。

因此，\(n\) 個人當中有某 \(2\) 個人同一天生日的機率為：

\(1 – \left( {\frac{{365}}{{365}} \times \frac{{364}}{{365}} \times \frac{{363}}{{365}} \times\cdots\times \frac{{365 – n + 1}}{{365}}} \right)\) 。

欲計算不同的 \(n\) 相對應的機率，除了可以利用計算機與電腦之外，我們還可以利用對數的概念與查表的方式，計算出上述各機率值。這裡先來看看人數為 \(4\) 個人時的例子。

首先，計算出四個人生日皆不同天的機率 \(\frac{{364}}{{365}} \cdot \frac{{363}}{{365}} \cdot \frac{{362}}{{365}}\)，這裡我們取常用對數：

\(\begin{array}{ll}\log (\frac{{364}}{{365}} \cdot \frac{{363}}{{365}} \cdot \frac{{362}}{{365}})&=\log 364+\log 363+\log 362-3\log 365 \\ &=\log (3.64 \cdot {10^2}) + \log (3.63 \cdot {10^2}) + \log (3.62 \cdot {10^2}) \\&~~~- 3 \cdot \log (3.65 \cdot {10^2})\\&=\log 3.64 + \log 3.63 + \log 3.62 – 3 \cdot \log 3.65\end{array}\)

Continue reading →

我們同一天生日（一）！（We have the same birthday!）
臺北市立和平高中黃俊瑋教師

生活中，許多人聚會的場合裡，不免會討論生日或星座問題。也許你會發現，當人數夠多時，總是會發生某兩人同一天生日的情況。特別是在同一個班級裡，人數動輒 \(40\) 人或更多時，總會有某兩個同學同一天生日，看起來非常不可思議。所謂有緣來相聚，這是巧合嗎？還是天註定？一群人裡，有某兩人要剛好同一天生日的機率直觀上似乎很低，但真是如此嗎？數學將帶你看穿真相！

以下，我們不考慮 \(2\) 月 \(29\) 日生日，僅考慮一年 \(365\) 天的一般情況。

首先，兩個人恰好在同一天生日的機率為 \(\frac{{C_1^{365}}}{{{{365}^2}}}\)，

亦即從一年 \(365\) 天當中選出一天將某這兩個人的生日塞進去。

或者你也可想成第一個人不指定哪一天，但第二個人必與第一個人同一天生日，

故機率為 \(\frac{{365}}{{365}} \cdot \frac{1}{{365}} = \frac{1}{{365}}\) 此值約為 \(0.0027\)。一片生日蛋糕（A piece of cake）！ Continue reading →

和算中的行列式(5)：拉普拉斯展開法（Determinants in Wasan (5): Laplace Expansion）
國立臺南第一高級中學林倉億老師

連結：和算中的行列式(4)：降階展開法

日本和算家對行列式展開的研究，在關孝和之後有了長足的進展。除了前文介紹過的井關知辰外，本文要介紹另一位和算家久留島義太 (Kurushima Yoshihiro, ?-1757)及其提出的行列式展開法，相當於今日所稱的「拉普拉斯 (Pierre-Simon Laplace, 1749-1827, 法國) 展開法」。

久留島義太屬於天才型的和算家，他對數學的認識並非來自老師的教導，而是從數學書《新篇塵劫記》中自學而來；後來與當時的和算家，特別是關流的和算家進行學術上的交流，豐富其數學研究的主題，並開拓新的研究領域，對後世和算的發展有著深遠的影響。因此，有人將他與關孝和、建部賢弘並稱為三大和算家。據後人的記載，久留島義太生性浪漫，雖然數學造詣很高，但沒有形成自己的門派，也沒有將著作出版，僅以稿本的形式在和算家間傳抄，身後留下《久氏遺書》一部。

Continue reading →

和算中的行列式(4)：降階展開法
（Determinants in Wasan (4): The Reductive Algorithm）
國立臺南第一高級中學林倉億老師

連結：和算中的行列式(3)：關孝和的《解伏題之法》（下）

關孝和提出相當於今日的行列式求法後，吸引不少和算家相繼投入研究，不僅改正了關孝和算法中的錯誤（當行列式是五階以上時，所求得的值是錯的），也提出了新的算法。本文要介紹的，就是相當於今日高中課堂上俗稱的「降階展開法」，也稱為「范德蒙 (Vandermonde, 1735-1796, 法國) 展開法」。

在目前可見的文獻中，最早寫出這個算法的是井關知辰 (Izeki Tomotoki)。井關知辰在1690年所著的《算法發揮》上卷中，用「陽率」來稱呼行列式，而「陰率」則是行列式展開後的結果。例如，「平陽率」、「立陽率」、「三陽率」分別代表二階、三階、四階行列式，「平陰率」、「立陰率」、「三陰率」則代表對應的行列式展開式。井關知辰在書中最高列出了「四陽率」與「四陰率」，也就是五階行列式及其展開式，並寫下如何展開更高階「陽率」的方法。  Continue reading →

和算中的行列式(3)：關孝和的《解伏題之法》（下）（Determinants in Wasan (3): Seki Takakazu’s Kai Fukudai no Ho (Methods of Solving Secret Questions), Part 2）
國立臺南第一高級中學林倉億老師

連結：和算中的行列式(2)：關孝和的《解伏題之法》（上）

〈和算中的行列式(2)：關孝和的《解伏題之法》（上）〉介紹了關孝和如何從解多元高次方程組中，發展出類似今日行列式的概念。然而，即便是今日，多元高次方程組求解仍是一件困難的工作。所以，關孝和能處理多元高次方程組，更顯得他在數學上的造詣深厚。以下透過幾個簡單的實例，讓讀者更熟悉關孝和的方法，也指出這個方法也有無能為力的時候。

例1：解 $$\left\{ \begin{array}{l} {(x – 1)^2} + {(y – 1)^2} = 1\\ {(x – 2)^2} + {(y – 2)^2} = 5\\ {(x – 3)^2} + {(y – 3)^2} = 13 \end{array} \right.$$。

【關孝和的方法】：

方程組可整理成 $$\left\{ \begin{array}{l} ({y^2} – 2y + 1) – 2x + {x^2} = 0\\ ({y^2} – 4y + 3) – 4x + {x^2} = 0\\ ({y^2} – 6y + 5) – 6x + {x^2} = 0 \end{array} \right.$$，

利用係數所成行列式 $$\left| {\begin{array}{*{20}{c}} {{y^2} – 2y + 1}&{ – 2}&1\\ {{y^2} – 4y + 3}&{ – 4}&1\\ {{y^2} – 6y + 5}&{ – 6}&1 \end{array}} \right| = 0$$，

但左式展開後各項均消去，得到 $$0=0$$ 的恆等式，而非 $$y$$ 的方程式，因此無從求 $$y$$ 之值。 Continue reading →

和算中的行列式(2)：關孝和的《解伏題之法》（上）
（Determinants in Wasan (2): Seki Takakazu’s Kai Fukudai no Ho (Methods of Solving Secret Questions), Part 1）
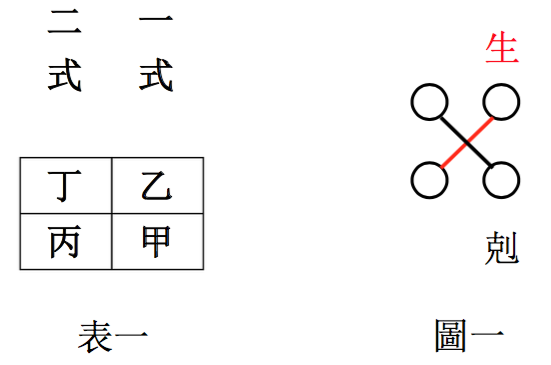
國立臺南第一高級中學林倉億老師

連結：和算中的行列式(1)：創立者關孝和

關孝和《解伏題之法》(1683年)的主要內容是解多元高次方程組。他提出了六個步驟：真虛、兩式、定乘、換式、生剋、寄消。其中的第五個步驟「生剋」，就相當於今日將行列式展開的過程，其「生」（以紅色表示）、「剋」（以黑色表示）就是在決定展開後每一項的正、負號。以今日的術語來說，關孝和在書中提出相當於將二至五階行列式展開的方法，並寫下二至四階的行列式展開式。

以二階行列式為例，關孝和呈現的方式如下表一，

然後說乙丙相乘是「生」，丁甲相乘是「剋」，

用今日符號表示的話，就是 

關孝和還用下圖一來表示這規則。

Continue reading →