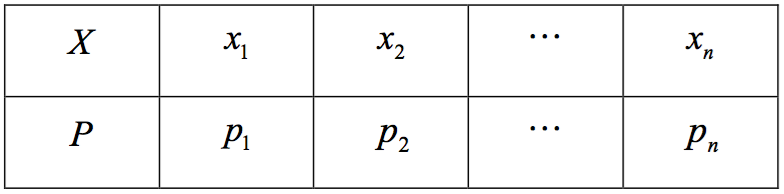三角函數圖形的平移與伸縮
臺北市立西松高中 蘇惠玉教師

在將角度轉換成弧度之後，對於實數 \(x\)，我們都可以將其考慮成弧度，進一步定義它的某個三角函數值。例如正弦函數，對每一個實數 \(x\)，定義 \(f(x)=\sin x\)。定義完六個三角函數之後，可以利用描點的方式繪出函數圖形。

例如 \(y=f(x)=\sin x\) 的圖形如下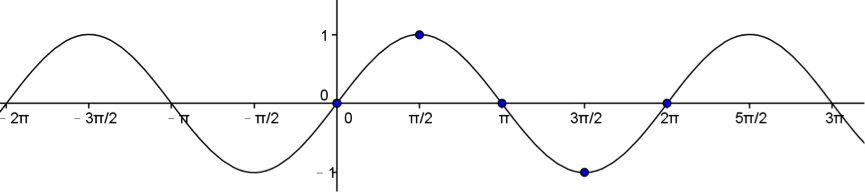：    接下來，筆者將以 \(f(x)=\sin x\) 的圖形為例，來說明三角函數圖形的平移與伸縮如何作圖，

以及平移與伸縮對圖形的基本特徵如週期、振幅與極值的影響。 Continue reading →

二階方陣的分解(The Decomposition of 2-by-2 matrices)
臺北市立第一女子中學數學科蘇俊鴻老師

誠如〈平面上的線性變換〉一文所言，平面上的線性變換都會對應到唯一的二階方陣。因此，透過二階方陣分解成基本矩陣的乘積，我們就能了解這個方陣所對應的線性變換是由那些基本變換所合成，這也是本文最主要的內容。

想要將一個方陣進行分解，我們得從矩陣的列運算談起，矩陣的列運算有下面三種：

1. 將一矩陣的某一列乘上某一數值加入另一列。
2. 將一矩陣的某一列乘以一個不為0的數。
3. 將一矩陣的某一列中的某兩列互換位置。

事實上，對矩陣 $$M = \left[ {\begin{array}{*{20}{c}} a&b\\ c&d \end{array}} \right]$$ 進行列運算的結果，等價於將矩陣 $$M$$ 乘上某些特殊矩陣 Continue reading →

平面上基本的線性變換：旋轉、鏡射、伸縮、推移 (Linear Transformations on the Plane: Rotation, Reflection, Scaling, Shear)
臺北市立第一女子中學數學科蘇俊鴻老師

平面上的線性變換，最基本的是下列的四種：旋轉、鏡射、伸縮、推移。本文將介紹這四種線性變換，及其所對應表示的矩陣。首先，由旋轉變換看起。

旋轉變換

如圖一，坐標平面上，\(\overline{OP}=r\)，且點 \(P(x,y)\) 滿足  \(x=r\cos\alpha,~y=r\sin\alpha\)。

那麼，以原點 \(O\) 為中心，將點依逆時針方向旋轉 \(\theta\) 角後得點 \(P'(x’,y’)\)。

那麼 \( \begin{cases} x’=r\cos(\alpha+\theta) \\ y’=r\sin(\alpha+\theta) \end{cases} \Rightarrow \begin{cases} x’=r(\cos \alpha \cos \theta – \sin \alpha \sin \theta) =x\cos \theta-y \sin\theta\\ y’=r(\sin \alpha\cos \theta+\cos \alpha\sin \theta)=y\cos\theta+x\sin\theta \end{cases}\)

若以矩陣表示，\(\left[ {\begin{array}{*{20}{c}} {x’}\\ {y’} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ – \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right]\) 。

因此，以原點 \(O\) 為中心逆時針方向旋轉 \(\theta\) 角的線性變換之表示矩陣為 \(\left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ – \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right]\) ，

並且將 \(\left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ – \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right]\) 稱為旋轉矩陣。

例如，將點 \(A(2,-4)\) 以 \(O\) 為中心逆時針旋轉 60^o，

則 \(\left[ {\begin{array}{*{20}{c}} {\cos {{60}^ \circ }}&{ – \sin {{60}^ \circ }}\\ {\sin {{60}^ \circ }}&{\cos {{60}^ \circ }} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 2\\ { – 4} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}}&{ – \frac{{\sqrt 3 }}{2}}\\ {\frac{{\sqrt 3 }}{2}}&{\frac{1}{2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 2\\ { – 4} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1 + 2\sqrt 3 }\\ { – 2 + \sqrt 3 } \end{array}} \right]\) ，

因此，對應點 \(A’\) 的坐標為 \((1+2\sqrt{3},-2+\sqrt{3})\)。 Continue reading →

平面上的線性變換(Linear Transformations on the Plane)
臺北市立第一女子中學數學科蘇俊鴻老師

矩陣是線性代數、離散數學、多變量微積分、多變量統計分析的基本工具。在高中課程中，對於矩陣的認識大致有兩種面向：首先，矩陣可以視為由許多數字組合而成的矩形陣列，可以一次處理大量的數字，例如一次聯立方程式與矩陣的關係、轉移矩陣的應用。此外，矩陣的加法和減法的運算規則也都證實這個觀點。另外，還有一個較為高階的觀點，就是將矩陣視為兩向量空間的線性變換之表達形式，這也使得矩陣成為線性代數主要處理的基本數學物件(object)。 Continue reading →

線性規劃(Linear Programming)
臺北市立第一女子中學數學科蘇俊鴻老師

讓我們就從下面的例子說起，來介紹什麼是線性規劃：

為預防禽流感，營養師吩咐雞場主人每天必須從飼料中提供至少 84 單位的營養素 A 、
至少 72 單位的營養素 B 和至少 60 單位的營養素 C 給他的雞群。

這三種營養素可由兩種飼料中獲得，且知第一種飼料每公斤售價 5 元並含有 7 單位的營 養素 A ，3 單位的營養素 B 與 3 單位的營養素 C ；第二種飼料每公斤售價 4 元並含有 2 單位的營養素 A ， 6 單位的營養素 B 與 2 單位的營養素 C 。

若雞場主人每天使用 x 公斤的第一種飼料與 y 公斤的第二種飼料就能符合營養師吩咐，並且想以最少的飼料成本來達到雞群的營養要求，則x, y 的值為何？最少的飼料成本又是多少？

換言之，雞場主人想要以「最少」的飼料成本來達成雞群的營養要求，以達到預防禽流感的目的；將成本寫成算式，就稱為目標函數。

該如何配置這兩種飼料的使用？首先，我們當然要先了解各種條件的限制。若是依條件列出的算式，以及「目標函數」都是一次式，我們就將此類的問題稱為「線性規劃」。

以上述問題來看，設每天使用第一種飼料 \(x\) 公斤；第二種飼料 \(y\) 公斤，

將條件列出，可得二元一次聯立不等式 \(\left\{ \begin{array}{l} x \ge 0,y \ge 0\\ 7x + 2y \ge 84\\ x + 2y \ge 24\\ 3x + 2y \ge 60 \end{array} \right.\) 。

同時，目標函數(即飼料成本)為 \(5x+4y\) 。這個問題便是典型的線性規劃問題。

進而，我們將滿足聯立不等式的解區域畫出，稱為可行解區域，如圖一。 Continue reading →

二元一次不等式(Two-Variable Inequalities)
臺北市立第一女子中學數學科蘇俊鴻老師

若 $$a,b,c$$ 為實數，且 $$a,b$$ 不同時為0，則稱 $$ax+by+c=0$$ 為二元一次方程式；

又因為它的圖形為一直線，也稱為直線方程式。

圖一正是二元一次方程式 $$2x+y=2$$ 的圖形。事實上，直線 $$2x+y=2$$ 上的任一點，

其坐標 $$(x,y)$$ 都滿足方程式 $$2x+y=2$$，換言之，都是方程式 $$2x+y=2$$ 的解。

因此，當點 $$P$$ 的 $$x$$ 坐標為 $$x_0$$ ，易推得 $$y$$ 坐標為 $$2-2x_0$$ 。

Continue reading →

數學期望值 (Mathematical Expectation)
國立屏東高級中學數學科楊瓊茹老師

在處理有關財務風險的事務時，不免要衡量可能的得與失，「數學期望值」的觀念在此時就顯得特別重要，可以幫助我們思考及判斷出最佳的決策。其定義如下：

若隨機變數 \(X\) 的機率分布如下表﹕

則稱 \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + \cdots + {x_n}{p_n} = \sum\limits_{i = 1}^n {{x_i}{p_i}} \) 為隨機變數 \(X\) 的數學期望值。

數學期望值 (簡稱期望值) 即平均值的概念，而且是加權平均數。將每個結果依它發生的機率來加權，發生機率愈大，權數愈高。 Continue reading →

機率法則 (Principle of Probability) (二)
國立屏東高級中學數學科楊瓊茹老師

連結：機率法則 (Principle of Probability) (一)

1993年美國奧克拉荷馬州突沙市 (Tulsa, Oklahoma) 法庭根據DNA鑑定報告等相關證物，判決提摩西‧杜朗犯下強暴與強盜罪。即便有十一個證人作證在案發時，提摩西正在達拉斯州參加飛靶射擊比賽，但是犯罪現場採得的DNA卻與提摩西的DNA吻合，在這項強力的證據下，求處刑期3200年。

究竟DNA鑑定比對的準確率有多高？高達 $$999,999/1,000,000$$ ！隨便一個人的DNA與犯罪現場的採樣相同的機率小於百萬分之一，甚至是億萬分之一，相同的可能性可以說是微乎其微。 Continue reading →