- 阿爾•卡西與圓周率(Jamshīd al-Kāshī and the measurement of π) 2013/10/17
阿爾•卡西與圓周率(Jamshīd al-Kāshī and the measurement of π)
臺北市立成功高中陳彥宏老師一、前言
圓周率 $$\pi$$ 的估算,一直是人類深感興趣的題材。從數千年前開始,數學家便設法要去計算 $$\pi$$ 值的大小。直到西元前三世紀,希臘科學家阿基米德 (Archimedes,西元前287-前212) 首度利用科學的方法計算 $$\pi$$ 的近似值,歷史上一連串計算圓周率 $$\pi$$ 的旅程便就此展開。在這漫長的旅途上,有一位不容忽視的伊斯蘭數學家-阿爾‧卡西 (Jamshīd al-Kāshī,?-1429),他所求得的 $$\pi$$ 的近似值能夠精確到小數點以下第十六位!本文將簡單介紹阿爾‧卡西計算 $$\pi$$ 所使用的方法,希望讀者能夠對這位阿拉伯的計算奇才有初步的認識。
二、生平
現今對於阿爾‧卡西最早的紀錄是在1406年,由其著作中得知,當時他開始在家鄉卡撒 (Kāshān,在今伊朗德黑蘭南方200公里) 進行一系列的月蝕觀測活動,在此之前,我們對他則一無所知。早期阿爾‧卡西的生活過得並不富裕,以致到處流浪兼職來謀生,直到1418年,他才在撒馬爾干 (Samarkand,在今烏茲別克境內) 的一所學校內謀得職位,這所學校正是由他一生中最大的資助者Sultan Ulūgh Beg創辦。同一時間,阿爾‧卡西開始對於數學有極重大的貢獻,1424年,他逼近圓周率 $$\pi$$ 的近似值精確至小數點以下第十六位,1427年他撰寫了關於算術、代數及測量的作品《算數者之鑰》(The Calculators’ Key),書中對於十進位記數系統、數的開高次方根及求解代數問題皆有詳細論述。此外,阿爾‧卡西還利用求解三次方程式得到正弦函數 $$\sin 1^\circ$$ 的近似值,而這也是他在1429年過世前的最後作品。
Continue reading →- 用向量來看圓系(Use Vectors to Understand Family of Circles)(1) 2013/10/11
用向量來看圓系(Use Vectors to Understand Family of Circles)(1)
臺北市立第一女子中學數學科蘇俊鴻老師在圓與直線的章節中,常有這樣的難題:
過兩圓 \(C_1:x^2+y^2+4x-6y-12=0\) 與 \(C_2: x^2+y^2-2x+2y-18=0\)
的交點,求圓心在 \(x+y+1=0\) 上的圓方程式。
一種可能的作法是先找出 \(C_1\) 與 \(C_2\) 的交點,再設法求所找之圓的圓心坐標及半徑,解法如下:
首先,解聯立方程組 \(\left\{ \begin{array}{l} {x^2} + {y^2} + 4x – 6y – 12 = 0 \cdots \cdots (1)\\ {x^2} + {y^2} – 2x + 2y – 18 = 0 \cdots \cdots (2)\end{array} \right.\)
由 \((1)(2)\) 可得,過兩圓交點的直線為 \(\displaystyle{3x} – 4y + 3 = 0 \Rightarrow x = \frac{{4y – 3}}{3}\),
代入 \((2)\) 式,得
\({(\frac{{4y – 3}}{3})^2} + {y^2} – 2(\frac{{4y – 3}}{3}) + 2y – 18 = 0\)
\(\Rightarrow 5{y^2} – 6y – 27 = 0 \Rightarrow y = 3\) 或 \(y=-\frac{9}{5}\)
當 \(y=3\) 時,則 \(x=3\);當 \(y=-\frac{9}{5}\),則 \(x=-\frac{17}{5}\)
因此,交點坐標為 \(A(3,3)\) 及 \(B(-\frac{17}{5},-\frac{9}{5})\),且弦 \(\overline{AB}\) 的中點為 \((-\frac{1}{5},\frac{3}{5})\)
\(\therefore\) 弦 \(\overline{AB}\) 的中垂線方程式為 \(4x+3y-1=0\)
而所求之圓的圓心為 \(x+y+1=0\) 及弦 \(\overline{AB}\) 的中垂線之交點,
解聯立方程組 \(\left\{ \begin{array}{l} 4x + 3y – 1 = 0\\ x + y + 1 = 0 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x = 4\\ y = – 5 \end{array} \right.\),
所求之圓的圓心為 \(O(4,-5)\),半徑 \(r=\overline{OA}=\sqrt{65}\)
因此,所求之圓的方程式為 \((x-4)^2+(y+5)^2=65\)
- 從托勒密定理到和角公式 (From Ptolemy Theorem to Angle sum and difference identities) 2013/10/11
從托勒密定理到和角公式 (From Ptolemy Theorem to Angle sum and difference identities)
臺北市立第一女子中學數學科蘇俊鴻老師在高中課程的三角函數單元提及了許多三角公式,像和(差)角公式、倍角公式及半角公式。事實上,這些三角公式(主要是正弦和餘弦函數)都是托勒密(C. Ptolemy, c. 100-178 C.E.)在發展弦表的過程中,提出的一系列命題(有興趣的讀者可參見《The Almagest》一書)。
從課程的安排上,不難發現和角與差角公式處於非常基礎的地位,這個現象在托勒密提出的脈絡中也是相符。然而,托勒密如何發現和角公式?若要讀者好奇地往前追溯,將會驚奇地發現和角公式和托勒密定理有著密切的關係。因此,從托勒密定理出發,也是介紹和角公式一個很好的切入點。 Continue reading →
- 點到直線的距離公式 2013/10/11
點到直線的距離公式 (The Formula of the distance from a point to a line)
臺北市立第一女子中學數學科蘇俊鴻老師99課綱中將圓與直線的單元放在平面向量之前,進而討論圓與直線的關係時,特別強調運用圓與直線的聯立方程式之解的形態(相等實根、兩相異實根,及沒有實根) 的「代數判定」方法。儘管此法的使用具有一般性,但計算通常較為繁雜。因此,老師通常還會介紹點到直線的距離公式,利用圓心與直線的距離來判斷兩者的關係。
然而,此距離公式的介紹常借助向量方法進行證明,使得許多老師倡議將圓與直線與平面向量兩個單元互換。不過,僅僅為了一個公式的證明大費周章,並且,更動後也涉及平面上直線的向量表示和直線方程式之間的調整問題。本文中提出幾個在99課綱中無須調動次序,也可達到證明點到直線的距離公式之目標的證法。 Continue reading →
- 正弦定律 (The Sine Law) 2013/10/11
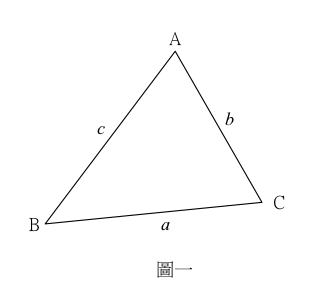
正弦定律 (The Sine Law)
臺北市立第一女子中學數學科蘇俊鴻老師在現行高中課程中,對於正弦定律的推導常是透過三角形面積公式為媒介:
如圖一,給定三角形 \(\Delta ABC\) ,則三角形 \(\Delta ABC\) 的面積為
\(\displaystyle\frac{1}{2}ab\sin C = \frac{1}{2}ac\sin B = \frac{1}{2}bc\sin A\)
因此,\(\displaystyle\frac{{\sin C}}{c} = \frac{{\sin B}}{b} = \frac{{\sin A}}{a} \Rightarrow \frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
- 輾轉相除法(IV) (Euclidean algorithm) 2013/10/07
輾轉相除法(IV) (Euclidean algorithm)
國立蘭陽女中數學科陳敏晧老師連結:輾轉相除法(III)
一、五猴分桃問題:
五隻猴子分一堆桃子,怎麼分也不能均分成五份,大家約定先去睡覺,明天再說。夜裡,猴甲偷偷起來,吃掉一個,這時發現其餘正好可以分成五份,結果猴甲把自己那份藏起來,又躺去睡覺了;接著猴乙也偷偷起來,吃掉一個,發現其餘也正好可以分成五份,結果猴乙也把自己那份藏起來;猴丙,猴丁,都如法炮製。而猴戊吃掉一個後,也發現餘桃數為 $$5$$ 的倍數。問總桃數最少有幾個?
參考解法:
假設總桃數為 $$x$$,而 $$y$$ 為某個正整數。
因為 $$\displaystyle\frac{1}{5}\left[ {\frac{4}{5}\left[ {\frac{4}{5}\left[ {\frac{4}{5}\left[ {\frac{4}{5}\left( {x – 1} \right) – 1} \right] – 1} \right] – 1} \right] – 1} \right] = y$$
整理方程式得:$$256x-3125y=2101$$ (此即為不定方程式),
利用歐幾里得的想法,我們先考慮 $$256x+3125y=1$$
$$\begin{array}{rl} 3125 &=12 \times 256+53\\256&=4\times 53+44\\53&=1\times 44+9\\44&=4\times 9+8\\9&=1\times 8+1\end{array}$$
- 輾轉相除法(III) (Euclidean algorithm) 2013/10/07
輾轉相除法(III) (Euclidean algorithm)
國立蘭陽女中數學科陳敏晧老師連結:輾轉相除法(II)
一、輾轉相除法與連分數
首先讓我們來練習一下輾轉相除法,求 $$(42897, 18644)=\underline{~~~~~~~~~~~~~~~}$$。
(1)橫式過程:$$42897=2\times 18644+5609$$
$$18644=3\times 5609+1817$$
$$5609=3\times 1817+158$$
$$1817=11\times 158+79$$
$$158=2\times 79+0$$$$\therefore \left( {42897,18644} \right) = \left( {18644,5609} \right) = \left( {5609,1817} \right) = \left( {1817,158} \right) = \left( {158,79} \right) = \left( {79,0} \right) = 79$$
Continue reading →
- 輾轉相除法(II) (Euclidean algorithm) 2013/10/07
輾轉相除法(II) (Euclidean algorithm)
國立蘭陽女中數學科陳敏晧老師連結:輾轉相除法(I)
一、畢氏音律與輾轉相減法
 西元前五百多年,畢達哥拉斯(Pythagoras of Samos, c. 570 BC – c. 495 BC)(如右圖)為了探求音律,利用單弦琴(monochord)作實驗,發現兩個音的弦長為簡單整數比時,是和諧悅耳的。例如:$$2:1$$,$$3:2$$,$$4:3$$,$$5:4$$ 分別是八度、五度、四度及三度音程。這些弦長的比是如何求得的呢?若是分成 $$3:2$$,則會產生悅耳的和弦音樂,因此,不同的弦長比例會導致不同的音高,若是比例不正確,則會形成不和諧的和弦聲。
西元前五百多年,畢達哥拉斯(Pythagoras of Samos, c. 570 BC – c. 495 BC)(如右圖)為了探求音律,利用單弦琴(monochord)作實驗,發現兩個音的弦長為簡單整數比時,是和諧悅耳的。例如:$$2:1$$,$$3:2$$,$$4:3$$,$$5:4$$ 分別是八度、五度、四度及三度音程。這些弦長的比是如何求得的呢?若是分成 $$3:2$$,則會產生悅耳的和弦音樂,因此,不同的弦長比例會導致不同的音高,若是比例不正確,則會形成不和諧的和弦聲。原來畢達哥拉斯是利用逐步相減法(the successive subtraction)求得的:考慮 $$a$$、$$b$$ 兩弦,不妨設 $$a>b$$,從 $$a$$ 減去較小的 $$b$$,得 $$a-b$$;若 $$a-b$$ 仍大於 $$b$$,再減去 $$b$$ 得 $$a-2b$$;…,直到 $$a-tb\le b$$,其中 $$t\in\mathbb{N}$$。繼續從較大的 $$b$$ 減去較小的 $$a-tb$$,…,直到 $$b-l(a-tb)\le a-tb$$,其中$$l\in\mathbb{N}$$。按此要領反覆做下去,經過有限步的輾轉相減後,必可得到 $$0$$,此時運算停止。在 $$0$$ 之前最後一個不為 $$0$$ 的數 $$d$$,即最大公因數 $$d$$。
畢達哥拉斯相信,任意給定兩正整數 $$a$$、$$b$$,必可利用有限次的逐步相減運算,找到最後一個不為 $$0$$ 的正整數 $$d$$,所以,存在正整數 $$p$$、$$q$$,使得 $$a=pd~, b=qd$$,而 $$d$$ 為滿足此式的最大弦長,從而得到 $$a:b =p:q$$ 為整數比,我們稱這種演算法稱為輾轉相減法。 Continue reading →
- 用向量來看圓系(Use Vectors to Understand Family of Circles)(1) 2013/10/11
Insert math as
Additional settings
Formula color
Type math using LaTeX
Preview
\({}\)
Nothing to preview
Insert