- 何處停車?物理學家的停車策略 2020/10/22
何處停車?物理學家的停車策略
鮑彥滕當騎著U-bike到停車站時,面對眼前的這個空位,究竟是要放棄它繼續往下騎,期待著離捷運出口更近的空位,但卻會冒著其他位置都滿,結果只能被迫折返的風險呢,還是保守的選擇它,但看見後面滿滿的空位,最後懊悔自己多走了一大段路。究竟怎樣的選擇是最有效率的? 波斯頓大學的兩位統計物理學家Krapivsky和Redner 在Journal of Statistical Mechanics上發表了他們的研究。
在Krapivsky和Redner的模型中,他們以時間花費作為衡量效率的量尺。當然,離目的地最近的車位可以走最少的路,但可能要多耗費折返的時間來發現它。於是駕駛員面對空位的取捨影響了他們停完車再走到目的地需要耗費的時間。Redner 說:「數學讓你能做最聰明的選擇,它讓你能洞悉這個複雜的世界」。 Continue reading →
- 微積分的dx(二):從級數到函數論 2020/09/23
微積分的dx(二):從級數到函數論
李龍欣上回我們簡單介紹了「無限小」的概念,而這回我們將時光倒流,看看在微積分剛剛發明後的大約100年期間的樣貌,以及這100年之後催生出的「極限」的概念,以及於此同時,質疑「函數」的思潮。
●十七、十八世紀的微積分
17世紀中期微積分發明之後,有許多未解的問題得到重大突破。例如在幾何方面,本來只能處理二次曲線的問題,但微積分用在其他曲線也有用。在處理過這些問題後,有很多曲線都可以寫成幂級數 (power series)──簡單來說就是把多項式變成無限多項。例如:
\(\tan^{-1}(x)=x-\frac{1}{3}x^3+\frac{1}{5}x^5-\frac{1}{7}x^7+\cdots\)
\(\cos(x)=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+\cdots\)
牛頓在分類三次曲線時尚須借助微積分,微積分又能處理無限多項的多項式,多麼振奮人心啊!也難怪 布魯克·泰勒(Brook Taylor,1685─1731) 會想要把所有函數都變成幂級數,而這個幂級數稱為泰勒展開式 (Taylor expansion):
\(f(x)=\frac{1}{0!}f(a)+\frac{1}{1!}\frac{df}{dx}(a)(x-a)+\frac{1}{2!}\frac{d^2f}{dx^2}(a)(x-a)^2+\frac{1}{3!}\frac{d^3f}{dx^3}(a)(x-a)^3+\cdots\)
順帶一提,列翁哈特·歐拉(Leonhard Euler,1707─1783) 對於無限多個數相加這件事有獨到的見解。幂級數在他手中能有千變萬化,甚至能夠因式分解。
可是幂級數並沒有那麼美好。例如我們知道等比級數的公式
\(1+r+r^2+\cdots=\frac{1}{1-r}\)
歐拉注意到以下的推論 (分別代入 \(r=n\) 和 \(r=1/n\)) 不合理:
\((\cdots+\frac{1}{n^2}+\frac{1}{n}+1+n+n^2+\cdots)=-1+(1+n+n^2+\cdots)+(1+\frac{1}{n}+\frac{1}{n^2}+\cdots)\)
\(=-1+\frac{1}{1-n}+\frac{1}{1-\frac{1}{n}}=0\)
桂斗·格然迪(Guido Grandi,1671─1742) 也注意到在等比級數中代入 \(r=-1\) 的話會得到
\(\frac{1}{2}=(1-1+1-1+\cdots)=((1-1)+(1-1)+\cdots)=(0+0+\cdots)=0\)
這幾個例子都顯示出我們要更嚴肅地看待函數的運算。
●極限 (limit)
我們對於有限小的數做為分母、有限多個數相加都沒有問題,可是無限小的數做為分母、無限多個數相加本來就大有問題。時間回到18世紀的英國,詹姆士·朱林(James Jurin,1684─1750) 和 班哲明·羅賓斯(Benjamin Robins,1707─1751) 為首的兩派學者基於牛頓所提出的「極限」(limit) 的雛形展開筆戰,或許有影響到後人。歐陸方面,冉勒宏·達朗貝爾(Jean-le-Rond d’Alembert,1717─1783) 運用「極限」重新詮釋微分。譬如曲線 \(y=f(x)\) 上有兩個點 \((x,f(x))\) 和 \((x+\Delta x,f(x+\Delta x))\),將兩點連起來得到的直線稱為割線 (secant line)。當 \(\Delta x\) 越小,這條直線就越接近 \((x,f(x))\) 的切線 (tangent line),而割線的斜率也往切線的斜率靠近,而切線的斜率就是微分。
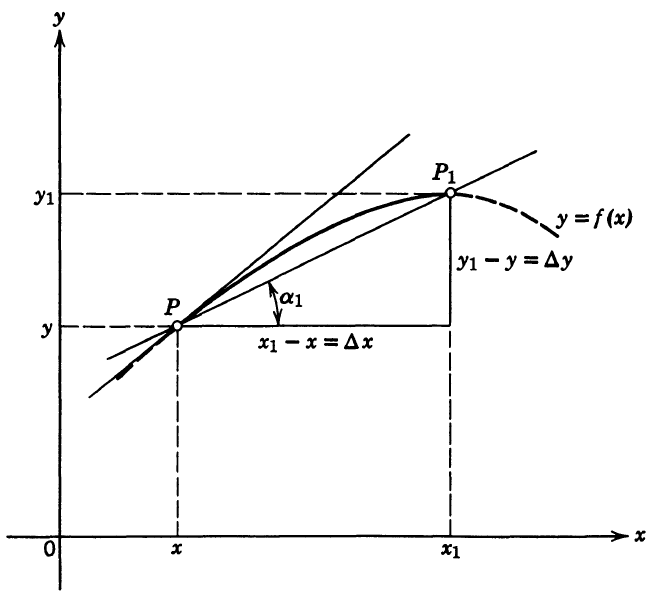
圖1:割線與切線。圖片來源:《Introduction to Calculus and Analysis》。R. Courant、F. John 著。初版(1989)。Springer-Verlag 出版(紐約/柏林/海德堡)
從有限小的 \(\Delta x\) 模擬無限小的 \(dx\),這就是「極限」。從算式中可以看出其對應關係:
\(\displaystyle\frac{df}{dx}=\lim\frac{\Delta f}{\Delta x}\)
來到了19世紀,奧古斯丁·柯西(Augustin Cauchy,1789─1857) 進一步詮釋,為了方便應用到證明中,在敘述時需要先假設我們知道割線的斜率靠近的是哪個數,再把這個數稱為割線斜率的極限。達朗貝爾、柯西用文字描述極限而有點拗口,後來 卡爾·外爾許特拉斯(Karl Weierstraß,1815─1897) 發明的「\(\varepsilon-\delta\)語言」敘述起來更精簡但精神相同。
至於積分方面,回到原本的方法,用長方形面積來估計圖形的面積。長方形的寬度為 \(\Delta x\)註1,高度和每一小段曲線的左端一樣高,如下圖所示:
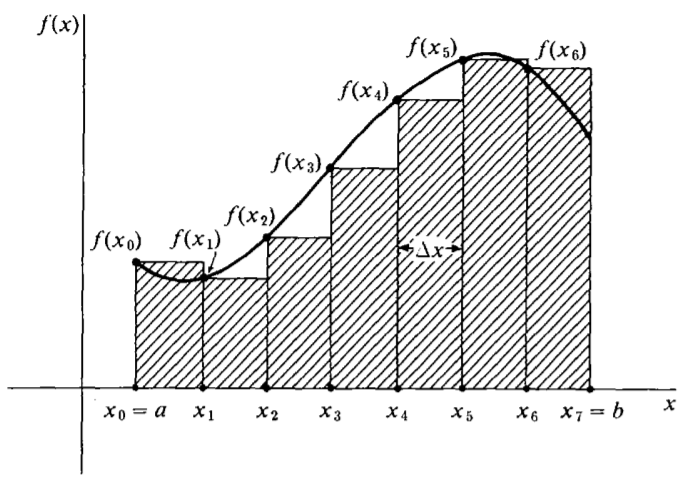
圖片來源:《Elementary Calculus: An Infinitesimal Approach》。H. Keisler 著。2019年9月修訂版。於網路免費公開。網址:http://www.math.wisc.edu/~keisler/calc.html。另有印刷版:第三版(2012)。Dover 出版(紐約)。
當 \(\Delta x\) 有限小、長方形有限多時的面積和稱為黎曼和 (Riemann sum)。當切割越來越細時,黎曼和的極限就是曲線下的面積。可以用算式表達為:
\(\displaystyle \int f(x)dx=\lim\sum f(x_i)\Delta x\)
同樣是用有限小的 \(\Delta x\) 模擬無限小的 \(dx\)。
●函數論 (theory of functions)
函數的意義從18世紀到19世紀經歷一大轉變。原本的函數所象徵的是「計算方法」,必需要是「可以算的」。後來發現函數能否計算、甚至是能否描述出來,似乎跟能否做微積分沒什麼關係了。因而需要針對能否做微積分的部分重新審視。例如下列兩個問題:
一、無窮和是否真的是數?哪些函數是幂級數?
為何要問這個問題?因為柯西發現一個泰勒展開式為 0 但原函數不是 0 的函數:
\(\displaystyle f(x)=\left\{\begin{array}{c} e^{-x^2} & \text{若}~x\neq 0 \\ 0 & \text{若}~x= 0\end{array}\right.\)
所以這個函數不是一個幂級數。
以一個幂級數
\(f(x)=A+B(x-a)+C(x-a)^2+D(x-a)^3+\cdots\)
來說,當 \(|x-a|\) 越小註2,越有機會讓總和有限,而柯西也證明了確實如此。用柯西的根值檢驗法 (root test),可以找到收斂半徑 (radius of convergence)。在 \(|x-a|\) 小於收斂半徑時都能當做函數並且用18世紀的方法做微積分。反之,在 \(|x-a|\) 等於收斂半徑時一定會在某些點遇到總和為無限大的問題。
二、什麼函數可以積分?
柯西首先用極限描述積分之後,貝恩哈特·黎曼(Bernhard Riemann,1826─1866) 認為並沒有理由要用左端點,而改成用曲線上任一點,並且只有當任意取法都得到同一個極限時才算是可以積分。接下來又進一步試圖改進的有很多,主要有:昂里·勒貝格(Henri Lebesgue,1875─1941)、托馬斯·斯提爾切斯(Thomas Stieltjes,1856─1894)、約翰·拉董(Johann Radon,1887─1956)。各個理論的「能夠積分」的函數各自略有不同。
而這兩個問題也分別成為複變分析 (complex analysis)、實變分析 (real analysis) 的開端。
註解:
[1]在柯西和黎曼的定義中,長方形的寬度不必相等,但是必須在取極限時全部縮小至 0。
[2]兩直劃的記號為複數的絕對值。
參考資料:
- 《A History of Mathematics》。F. Cajori 著。第二版(1961)。Macmillan 出版(紐約)。
- 《A History of Mathematics》。U. Merzbach、C. Boyer 著。第三版(2011)。Wiley 出版(紐澤西)。
- 《The Calculus Gallery: Masterpieces from Newton to Lebesgue》。W. Dunham 著。初版(2005)。Princeton University Press 出版(紐澤西)。
- 〈Newton and Infinite Series〉。大英百科全書。於網路公開。網址:https://www.britannica.com/topic/Newton-and-Infinite-Series-1368282
- 阿爾•卡西與圓周率(Jamshīd al-Kāshī and the measurement of π) 2020/05/08
阿爾•卡西與圓周率(Jamshīd al-Kāshī and the measurement of π )
臺北市立成功高中陳彥宏老師/國立臺灣師範大學數學系洪萬生教授、林延輯教授責任編輯一、前言
圓周率π的估算,一直是人類深感興趣的題材。從數千年前開始,數學家便設法要去計算π值的大小。直到西元前三世紀,希臘科學家阿基米德 (Archimedes,西元前287-前212) 首度利用科學的方法計算π的近似值,歷史上一連串計算圓周率π的旅程便就此展開。在這漫長的旅途上,有一位不容忽視的伊斯蘭數學家-阿爾‧卡西 (Jamshīd al-Kāshī,?-1429),他所求得的π的近似值能夠精確到小數點以下第十六位!本文將簡單介紹阿爾‧卡西計算π所使用的方法,希望讀者能夠對這位阿拉伯的計算奇才有初步的認識。
二、生平
現今對於阿爾‧卡西最早的紀錄是在1406年,由其著作中得知,當時他開始在家鄉卡撒 (Kāshān,在今伊朗德黑蘭南方200公里) 進行一系列的月蝕觀測活動,在此之前,我們對他則一無所知。早期阿爾‧卡西的生活過得並不富裕,以致到處流浪兼職來謀生,直到1418年,他才在撒馬爾干 (Samarkand,在今烏茲別克境內) 的一所學校內謀得職位,這所學校正是由他一生中最大的資助者Sultan Ulūgh Beg創辦。同一時間,阿爾‧卡西開始對於數學有極重大的貢獻,1424年,他逼近圓周率π的近似值精確至小數點以下第十六位,1427年他撰寫了關於算術、代數及測量的作品《算數者之鑰》(The Calculators’ Key),書中對於十進位記數系統、數的開高次方根及求解代數問題皆有詳細論述。此外,阿爾‧卡西還利用求解三次方程式得到正弦函數 的近似值,而這也是他在1429年過世前的最後作品。
- 機率歷史(The History of Probability) 2020/04/20
機率歷史(The History of Probability)
國立蘭陽女中數學科陳敏晧老師/國立台灣師範大學數學系許志農教授責任編輯自古以來,對於不可預知的事情,人們總是充滿著好奇,並且在好奇心的驅使下,往往產生了一些或對或錯的法則。姑且不論其動機為何,這些法則卻可能因此開創另一領域或學科,機率論(theory of probability)的發展便是如此。
Continue reading →
- 微積分的dx(一):無限小數與非標準分析學 2020/01/01
微積分的dx(一):無限小數與非標準分析學
李龍欣17世紀時牛頓和萊布尼茲發明了微積分。其中萊布尼茲的「積分符號」\(\int\)、「極微小差」\(dx\) 等兩個符號仍然使用至今。現今的課本會用「極限」解釋,所以有些人說 \(dx\) 只是符號,不需要實質意義。這兩種觀點都有其意義和重要性。本文將分為若干期,從不同觀點探索微積分的靈魂、以及各觀點的應用。
●為何有微積分
自古以來,數學家們就深知自然萬物難以測量,而不如圓形、多邊形、橢圓一般簡潔。我們固然可以拿起一把尺開始耐著性子量,例如阿基米德 (Αρχιμήδης ο Συρακούσιος)、劉徽、關孝和 (関 孝和) 的割圓術,又譬如古巴比倫人的三角函數表,都是測量的典範和先驅。 Continue reading →
- 從牛頓的時代背景探索第二運動定律(下) 2018/03/28
從牛頓的時代背景探索第二運動定律(下)
行政院科技部科技顧問/瑞典林雪平大學榮譽教授 趙光安牛頓給力一個定義:第二運動定律
在伽利略和牛頓的時代,數學工具只有幾何、三角、和代數,物理知識也僅限日常生活中有系統的觀察,及少數的實驗結果。用現代的標準來衡量,伽利略和牛頓頂多只有國中畢業的程度。如果我們用現代的數理常識背景來解答三、四百年前的問題,那就是「事後有先見之明」了。雖然和「力學」有關的量測,伽利略得到的數據被推崇是權威性,然而他的「力學」實驗幾乎全部是基於物體的直線運動。在這個時代背景下,牛頓建立的理論,是從「一維系統」開始,然後才推廣到「三維空間」。因此,我們也從直線運動開始,試試看能否經歷一趟牛頓的思路。 Continue reading →
- 拉丁方設計介紹 2016/09/26
拉丁方設計介紹(Introduction of Latin Square Design)
國立臺灣大學農藝學系 黃昭惠一、原理
與《隨機完全區集設計介紹》一文所提及的 RCBD 隨機完全區集設計相同,拉丁方設計 (Latin Square Design, LSD) 也是一種與區集因子相關聯的設計方法,不同的是我們在中 RCBD 只有一個區集因子,稱為單向區集設計 (one-dimensional block),而 LSD 可以同時控制兩個區集因子的影響,故屬於兩向區集設計 (two-dimensional block),透過行區集與列區集的規劃(圖一),實驗者即可有效控制兩干擾因子的影響。 Continue reading →
- 隨機完全區集設計介紹 2016/09/24
隨機完全區集設計介紹(Introduction of Randomized Complete Block Design)
國立臺灣大學農藝學系 黃昭惠一、原理
進行試驗設計時,當我們的試驗單位為異質,也就是試驗單位的變異不平均時,我們會利用區集的劃分,去除這些已知變異因子對實驗造成的影響。
以山坡地進行牧草品種實驗為例,假設有 A、B 兩種品種於坡地上進行比較試驗,每種品種三重複,其實驗目的為檢驗此兩品種的牧草產量是否具有明顯的差異,根據地理知識已知下坡的土地應較為肥沃,草坪的生長應較為繁茂,若直接將兩品種隨機排列(圖一),則 B 品種可能因生長於較佳的環境,故有較好的表現,而非品種差異所造成,這樣的結果會導致實驗的誤差,並影響我們在決策上的判斷;若我們採用本章所介紹的隨機完全區集設計(randomized complete block design, 簡稱 RCBD)進行試驗(圖二),將土地依據已知造成試驗誤差的因素(坡度)分為三組(三個區集:B1、B2、B3),同組 (區集)內的土地相似,並在每組能同步施測兩品種,便可有效控制坡度因子對實驗結果的影響,準確估計出品種之間真正造成差異的幅度大小。 Continue reading →
- 微積分的dx(二):從級數到函數論 2020/09/23
Insert math as
Additional settings
Formula color
Type math using LaTeX
Preview
\({}\)
Nothing to preview
Insert

